Escalando unidades de conversión análoga-digitales es una técnica utilizada para convertir la magnitud física analógica en cualquier tipo de salida deseada.
En esta entrada intentaremos explicar una técnica matemática simple que utiliza las funciones recta como base , y a partir de ella será posible lograr que una señal analógica del mundo físico, como por ejemplo la salida de un sensor o transductor, a partir de sus unidades de conversión digital, sean escaladas al tipo de salida deseado. Por ejemplo un sensor de distancia , podrá representarse como una salida en metros o centímetros ( lo clásico) o por ejemplo en escala porcentual de 0 a 100%, o la escala que se desee, por ejemplo adimensional entre -70 y 70, es decir de acuerdo a lo que se desee. La condición fundamental es que el sensor o transductor sea lineal al menos en nuestro rango de uso. Este tipo de escalamiento se utiliza para manejar salidas mas acordes a nuestros requerimientos , en donde por ejemplo no sea de importancia el valor absoluto de la medición sino medidas relativas o en otro rango. Por ejemplo se desea controlar la temperatura de un horno, para lo cual se desea implementar un sistema que mantenga al mismo al 60% de su capacidad máxima.
Introducción al tema
Todas las magnitudes físicas de mundo real , presión, temperatura, volumen, nivel, velocidad, aceleración, caudal, distancia, desplazamientos, densidad, espesor, etc, necesitan de un conversor Análógico Digital «AD» para poder ingresar al mundo digital para su tratamiento. Históricamente y previo a los AD, el procesamiento era todo analógico y en determinadas aplicaciones lo sigue siendo. La interpretación de las magnitudes de salida y su cuantificación se resolvía con electrónica analógica. Por ejemplo un sensor de temperatura que entrega 0.5 volts a 25 oC y un sistema que necesitara generar valores de comparación para un lazo de control, se valía de la electrónica como divisores resistivos, amplificadores operacionales y demás componentes para poder comparar valores, lo cual generaba la problemática del ruido eléctrico y la precisión. Hoy en día los AD han permitido tratar digitalmente las magnitudes por medio de las unidades de conversión, y poder realizar posteriormente todas las comparaciones por medio de software digital, por ejemplo con microcontroladores.
Los conversores
Los que mas han ganado mercado son los AD que realizan sus operaciones de conversión utilizando la técnica de aproximaciones sucesivas, dado que son mas rápidos y el tiempo de conversión es fundamental en sistemas muestreados y sobre todo con señales de gran ancho de banda, es decir, señales rápidas que deben cumplir con el teorema de Niquist.
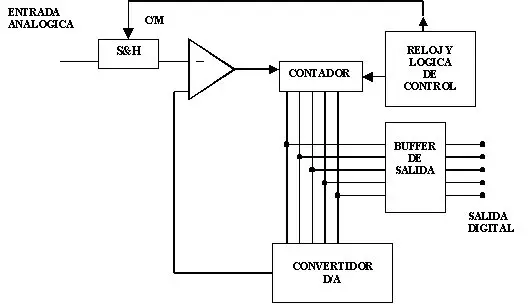
Sin entrar en demasiados detalles, la técnica consiste en un módulo de muestreo y retención S&H de la señal analógica de entrada la cual es comparada con un DAC o conversor digital analógico, el cual genera una tensión de salida de acuerdo a la cantidad de bits n que posea y a la cuenta del módulo contador , que recibe los pulsos de reloj desde el módulo de control . El contador se sitúa a la mitad de escala es decir a 2^n-1/2 , y el DAC lo convertirá en VREF/2. De acuerdo a la comparación, si es mayor o menor, se sabrá si el primer bit de conversión , el de mas peso será un 1 o un cero. El rango como se ve se va dividiendo de 2 en 2 , mitad hacia arriba o mitad hacia abajo , que a su vez se dividirá en 2 acotando así cada vez mas el rango y aproximándose al valor analógico.
Para ser didáctico por ejemplo piense un número del 1 al 100 y yo lo adivino. Supongamos que usted elige el 27. Por mi parte comienzo por indicar el 50 (contador) que es mitad de escala o rango , y usted me dice que mi número es mayor ( comparación). El rango está entre 0 y 50. Ahora yo contador divido la escala de abajo en 2, es decir 25 . Indico 25, usted me dice que es menor a su número, entonces ahora el rango queda acotado entre 25 y 50 , si el número hubiese sido por ejemplo el 23 mi rango sería entre 0 y 25. Ahora divido el rango 25-50 entre 2 , sería 25/2= 12.5 + 25 , es decir 37,5, indico 37. Usted me dice que es mayor , ahora el rango está entre 25 y 37 , y así siguiendo, de manera que el rango se va acotando hasta que el mismo sea indivisible y se llegue al número buscado. Este algoritmo se denomina búsqueda binaria y es utilizado siempre y cuando los valores de búsqueda estén ordenados.
La Conversión
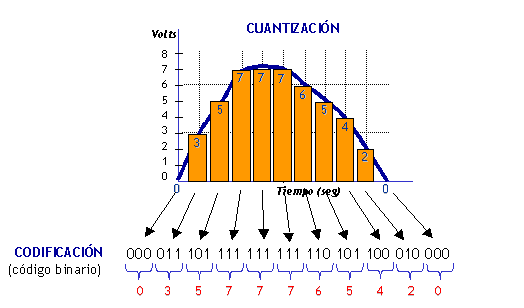
La conversión de un AD genera una salida binaria cuantificada que representa un rango de la señal de entrada. La señal de entrada es dividida en niveles de cuantificación determinados por la cantidad de bits del AD. Cuanto mayor sea la cantidad de bits , mayor será la cantidad de estados posibles y por lo tanto los rangos de cuantificación serán mas pequeños. Dado n bits, la cantidad de estados posibles es 2^n, es decir si por ejemplo n=3, los estados posibles o combinaciones utilizables son 8, para n=10, 1024. La siguiente figura muestra una cuantificación para n=3 bits:
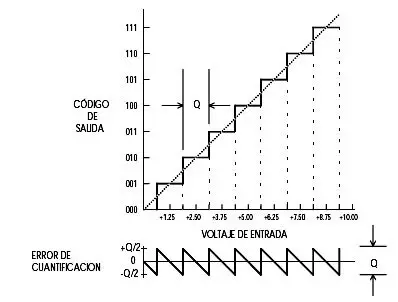
la señal de entrada posee un rango máximo de 10 volts , por lo tanto este rango será cuantificado en 8 estados, de manera que cada estado representará un rango de la entrada, denominado Resolución , que en este caso será, Rango Señal / 2^n = 10/8 = 1.25 v. Quiere decir que la entrada es representada por rangos discretos de 1.25 v. En este caso el AD trabaja de manera que el nivel de decisión se encuentre a la mitad de cada rango, esto es 0.625 v, por debajo será el estado de cuenta x , y por arriba el estado de cuenta x+1. De esta manera se minimiza el Error de cuantificación Q a la mitad. La resolución es lo mas pequeño que podrá discriminar el AD y al tomar la decisión, lo máximo que se podrá equivocar es en +/- una cuenta. Por ejemplo supongamos que la señal sea exactamente 0.625 v, el AD deberá optar por asignar la cuenta x o la x+1, es inevitable. La salida del AD entonces representará a la entrada en Unidades de conversión UC adimensionales y que de por si solas no dicen nada, por ejemplo 1o1 =5.
El escalado de las unidades
Vamos ahora al tema central, habiendo dado algunos conceptos introductorios. Vamos a representar en forma general la problemática
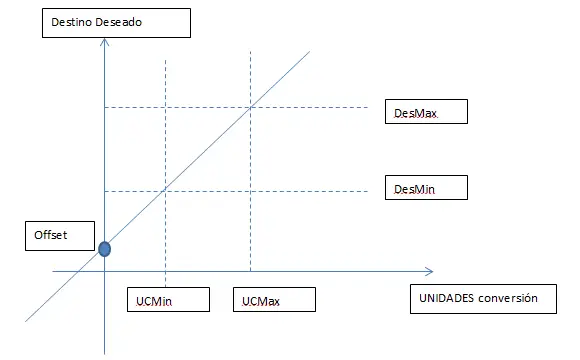
La gráfica representa la forma general de lo que nos encontraremos al trabajar con los AD.
- Destino Deseado , es la salida escalada deseada con su rango deseado
- Unidades de Conversión, es la salida del AD que se trabaja o Fuente de conversión
Rango deseado RD: DesMax-DesMin
Rango Conversión (RF rango fuente): UCMax-UCMin
La pendiente será m = RD/RF y la ecuación de la recta será entonces:
D = mU +Offset (1) , similar a y=mx+b , donde D será la variable salida deseada o destino deseado
y U la variable independiente de conversión.
Si para UCMin tenemos DesMin tenemos que: DesMin=m*UCMin +Offset
luego: Offset=b= DesMin-m*UCMin (2)
Sustituyendo (2) en (1) :
D=m*U +DesMin-m*UCMin
D=m*(U-UCMin) + DMin (3) con m = (DesMax-DesMin) / (UCMax-UCMin)
Esta ecuación fundamental para el escalamiento se suele citar en trabajos con módulos de programación de PLC’s y es muy útil desarrollarla para aplicaciones electrónicas con conversores AD, por tal motivo fue de importancia poder demostrar de donde sale para comprender su origen.
Ejemplos de Aplicación
Supongamos que tenemos un sensor de precisión de distancia que entrega una corriente de 4 a 20 ma para representar un rango entre 0 y 10 milímetros, para lo cual se utiliza un AD de 14 bits que trabaja entre -5v y +5v . Para convertir la corriente a tensión para la entrada de nuestro AD, colocamos un resistor de 220 Ohms de manera que:
4ma ——- 0.88v ( 4ma * 220 Ohm)
20 ma —— 4.4v (20ma * 220 Ohm) .
a) Deseamos representar la salida como lo que es , esto es en milímetros.
b) Deseamos representar la salida como porcentaje entre 0 y 100 %.
c) Deseamos representar la salida entre -100 y +100 unidades adimensionales.
Como primera medida vamos a encontrar los rangos :
CASO (a) :
RD = 10mm-0 = 10mm , DMin =0.
RC , debemos calcularlo, observar la siguiente figura:
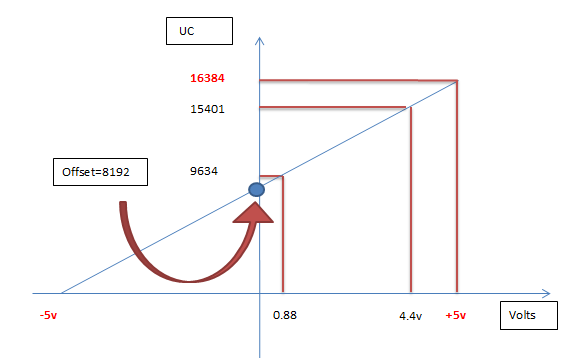
Aquí hemos construido la curva del sensor en relación con la del conversor AD. La ecuación del conversor es: UC = (2^14 /10)* V + offset . cuando V=-5, UC=0, luego Offset = 8192 Usando esta misma ecuación y reemplazando 0.88 y 4.4 volts , UCMin = 9634 y UCMax=15401.
De esta manera el RC = 15401-9634 = 5767 .
Aplicando ahora la función de escalamiento obtenemos:
Salida (mm) = (10/5767) * (UC-9634)
CASO (b):
RD= 100%-0% = 100 , DMin =0, RC = 5767
Salida (%) = (100/5767) * (UC-9634)
CASO (c):
RD = 200 , DMin = -100
Salida (adimensional) = (200/5767) * (UC-9634) – 100
Solo resta que estas soluciones se implementen dentro de nuestro algoritmo con el microcontrolador de nuestra preferencia.
Lo interesante de conocer el Rango de conversión RC es la posibilidad de asegurar que nuestros sensores trabajan correctamente, es decir al conocer UCMin y UCMax , por software podremos detectar si la conversión se va del rango en un determinado porcentaje previamente configurado. Es importante sobre todo en sistemas que utilizan muchos sensores y así poder determinar puntos de falla.
Bueno, espero les sea útil y hasta la próxima








gracias¡¡¡¡¡ super bien explicado y objetivo
Gracias a ti