En este post, vamos a explorar los diagramas de Bode, una herramienta muy útil para analizar el comportamiento de los sistemas a diferentes frecuencias. A lo largo del post, vamos a explicar qué son los diagramas de Bode, cómo se construyen y cómo se pueden utilizar para analizar el comportamiento de los sistemas.
También proporcionaremos un ejemplo práctico de cómo construir un diagrama de Bode a partir de una función de transferencia dada. Esperamos que encuentren este post útil y aprendan algo nuevo sobre los diagramas de Bode.
¿Qué es un diagrama de Bode?
Un diagrama de Bode es, por definición, una gráfica semi logarítimica de la magnitud (en decibeles) y de la fase (en grados) de una función de transferencia en función de la frecuencia.
¿Para qué se utiliza un diagrama de Bode?
Con los diagramas de Bode es posible representar gráficamente el comportamiento de un circuito eléctrico ante variaciones en la frecuencia de excitación. Es decir, cuando un circuito es sometido a señales de alimentación de frecuencia variable, se utiliza el diagrama de Bode para analizar la amplitud de la ganancia y la fase de las corrientes y los voltajes en el circuito.
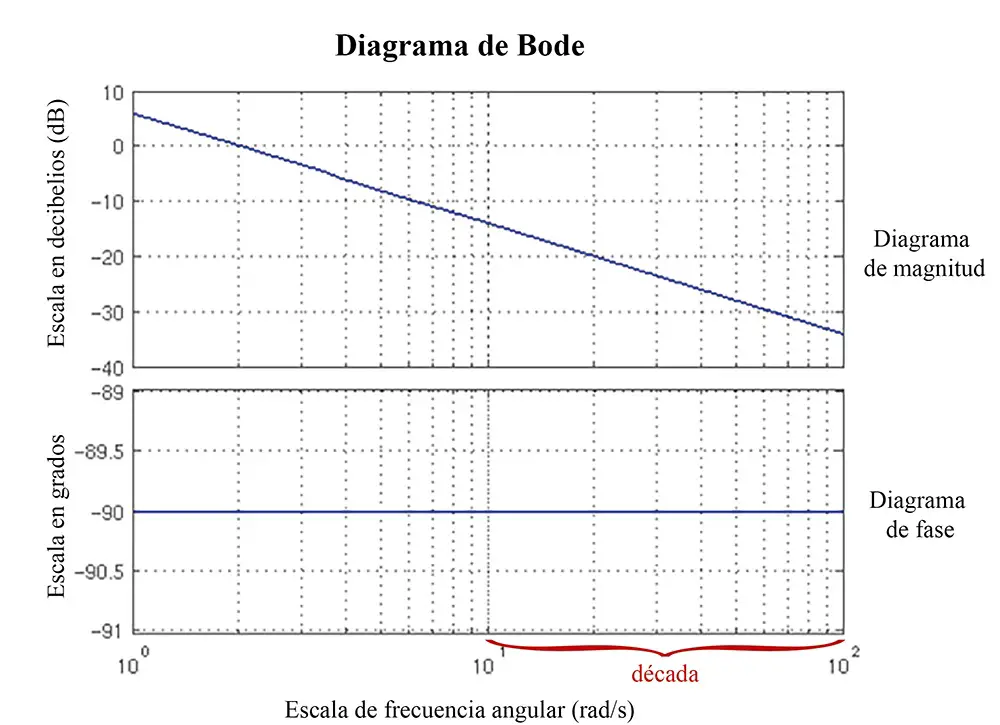
Los diagramas de Bode normalmente están compuestos por un diagrama de magnitud o de ganancia y un diagrama de fase, ambos dependientes de la frecuencia angular, denotada por ω. Debido a que esta frecuencia angular suele cubrir un amplio rango de valores, se acostumbra utilizar una escala logarítmica en el eje horizontal para una representación de la gráfica más fácil de analizar.
En el caso del Diagrama de Magnitud, el eje vertical está formado por la ganancia del circuito, dada en decibelios (dB). En el Diagrama de Fase, el eje vertical está formado por ángulos de desfase, dados en grados.
¿Cómo se construye un diagrama de Bode?
Los diagramas de Bode se construyen a partir de funciones de transferencia. Una función de transferencia es el resultado de dividir una salida entre una entrada en cualquier sistema. Por ejemplo, en el siguiente circuito:
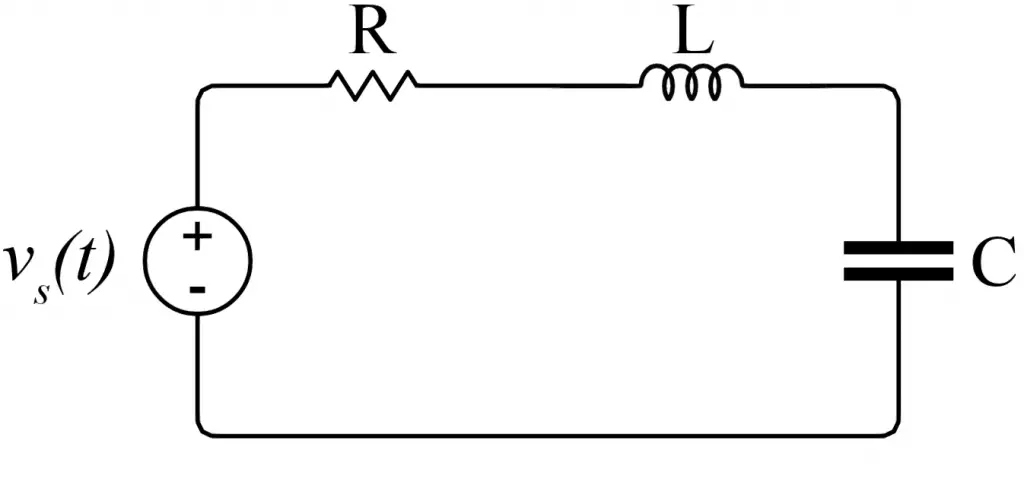
Este es un circuito RLC serie típico. De este circuito podemos obtener funciones de transferencia de voltaje, corriente y potencia, puesto que para nosotros estos son parámetros conocidos o calculables. De igual manera, se pueden obtener funciones de transferencia para cada uno de los tres elementos pasivos, sea la resistencia, el inductor o el capacitor. Por ejemplo, si queremos obtener la función:
Es decir, la función de transferencia que relaciona el voltaje de la resistencia con la fuente de poder. El voltaje de la resistencia sería la salida, mientras que el voltaje de la fuente es la entrada. Nótese que todo está en función de «s» y esto se debe a que las funciones de transferencia se obtienen en el dominio de la frecuencia compleja. Si pasamos el circuito al dominio de la frecuencia tendremos:
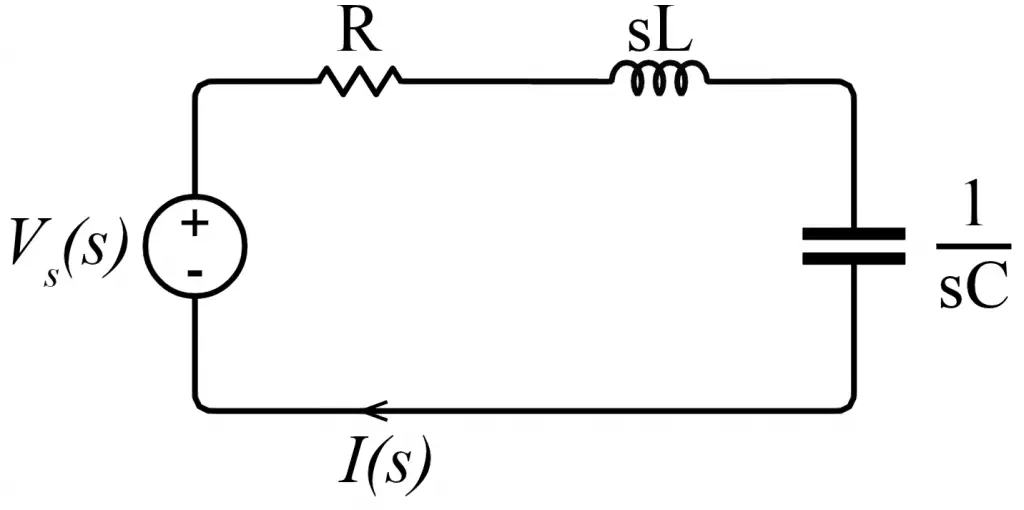
Si se desea obtener el voltaje en la resistencia se puede calcular la corriente I(s), para luego multiplicarla por R.
A partir de esta corriente se obtiene el voltaje sobre la resistencia:
Con este voltaje se puede obtener la función de transferencia H(s):
En el circuito mostrado también podríamos obtener funciones de transferencia relacionando el voltaje en el inductor o en el capacitor con respecto al voltaje de la fuente, que es la única señal de entrada del circuito. No tendría caso buscar funciones de transferencia de corriente en este circuito, puesto que todos los elementos están en serie y poseen una misma corriente. También se podría calcular una función de transferencia de potencia entre los cada elemento y la fuente de poder.
Debido a que las funciones de transferencia relacionan una salida entre una entrada, es posible a partir de una función de transferencia calcular la ganancia de un circuito. Y es por esta razón que en el gráfico de magnitud se utilizan decibelios para expresar la magnitud de la ganancia.
En los sistemas de comunicación, la ganancia se mide en bels. Históricamente, el
bel se usa para medir las relación entre dos niveles de potencia o la ganancia de potencia G.
El Bel es una magnitud muy grande para los sistemas con los que se trabaja comúnmente, por lo que casi siempre se trabaja con decibelios, los cuales son una décima parte de un Bel. La ganancia en decibelios se calcula utilizando:
Entonces, en resumen, los diagramas de Bode son un par de gráficos que representan la ganancia de un sistema y el desfase entre una señal de salida frente a una señal de entrada. La ganancia y el ángulo de desfase se obtienen a partir de una función de transferencia, para la cual se construye el diagrama de Bode.
Sin embargo, como el eje horizontal en los diagramas de Bode se utiliza una escala de frecuencia angular, esto quiere decir que las funciones de transferencia deben estar en función de la frecuencia angular y no en función de «s».
Debido a que los sistemas para los cuales se hace el análisis de Bode son excitados por fuentes del tipo senoidal o cosenoidal, es posible remplazar las «s» de la función de transferencia H(s) por «jω», donde «j» es el operador imaginario (raíz cuadrada de -1) y «ω» es la frecuencia angular del sistema, dada en rad/s. Así, expresamos la función de transferencia H(s) como H(jω):
Una vez se expresa la función de transferencia en función de jω se puede proceder a construir el diagrama de Bode.
Construcción de diagrama de Bode por aproximación asintótica
Para construir los diagramas de Bode a mano se utiliza una aproximación por medio del uso de asíntotas. Estas asíntotas se establecen con base en los polos y los ceros de la función de transferencia. La pendiente de las asíntotas depende del tipo de polos y ceros que forman la función de transferencia.
Para un mejor análisis de las funciones de transferencia es conveniente factorizar tanto el numerador como el denominador, de forma tal que sea posible apreciar la forma que tienen los polos y los ceros. Este procedimiento conviene hacerlo en función de «s». De esta manera. una función de transferencia podría verse de la siguiente manera:
De esta expresión podemos identificar 7 tipos de elementos que producen 7 pendientes distintas dentro del diagrama de Bode:
- Valores constantes (K)
- Cero en el origen (s)±n
- Cero simple (s+a)
- Cero cuadrático (s+b)2 ó (s2+2bs+b2)
- Polo en el origen (s)±n
- Polo simple (s+c)
- Polo cuadrático (s+d)2 ó (s2+2ds+d2)
Cada uno de estos elementos produce una pendiente distinta dentro del diagrama de Bode, tanto en magnitud como en fase.
- Valores constantes: producen tramos constantes en el diagrama de Bode, es decir, líneas con pendiente cero. En el diagrama de fase producen tramos con ángulo cero.
- Cero en el origen: Producen líneas con pendiente positiva, siendo esta igual a 20n decibelios por década. En el diagrama de fase producen rectas en 90nº
- Cero simple: producen líneas con pendiente positiva, siendo esta igual a 20 decibelios por década. La pendiente es positiva a partir de ω = a. En el diagrama de fase producen variaciones de 0 a 90º de forma lineal con pendiente positiva, de forma tal que cuando ω = 0.1a el desfase es 0º y cuando ω = 10a, el desfase será de 90º.
- Cero cuadrático: producen líneas con pendiente positiva, siendo esta igual a 40 decibelios por década. La pendiente es positiva a partir de ω = b. En el diagrama de fase producen variaciones de 0 a 180º de forma lineal con pendiente positiva, de forma tal que cuando ω = 0.1b el desfase es 0º y cuando ω = 10b, el desfase será de 180º.
- Polo en el origen: Producen líneas con pendiente negativa, siendo esta igual a 20n decibelios por década. En el diagrama de fase producen rectas en -n90º
- Polo simple (s+c): producen líneas con pendiente negativa, siendo esta igual a -20 decibeles por década. La pendiente es positiva a partir de ω = c. En el diagrama de fase producen variaciones de 0 a -90º de forma lineal con pendiente negativa, de forma tal que cuando ω = 0.1c el desfase es 0º y cuando ω = 10c, el desfase será de -90º.
- Polo cuadrático: producen líneas con pendiente negativa, siendo esta igual a -40 decibelios por década. La pendiente es positiva a partir de ω = d. En el diagrama de fase producen variaciones de 0 a -180º de forma lineal con pendiente negativa, de forma tal que cuando ω = 0.1d el desfase es 0º y cuando ω = 10d, el desfase será de -180º.
El comportamiento de los distintos tipos de polos y ceros se resume en la siguiente imagen:
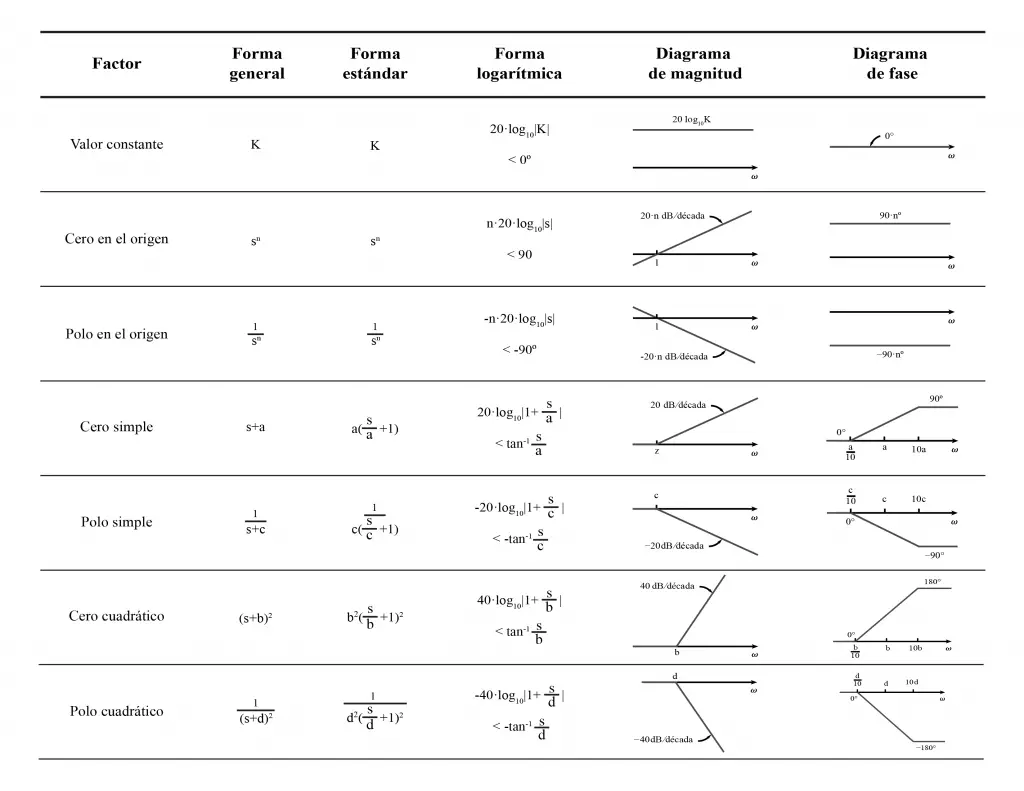
Con base en estas características es posible construir los diagramas de Bode estableciendo las asíntotas sobre una escala semilogarítmica.
Ejemplo de diagrama de Bode
Forma estándar de la función de transferencia
Para ilustrar los conceptos que hemos explorado hasta ahora, se propone construir el diagrama de Bode de magnitud y de fase para la siguiente función de transferencia:
Lo primero que se recomienda hacer es factorizar el numerador y el denominador para identificar la forma de los polos y los ceros.
Al factorizar se obtiene que esta función de transferencia posee:
- Una constante K
- Un cero en el origen
- Dos polos simples
Después de identificar los polos y los ceros, se procede a expresar la función de transferencia en la forma estándar. Con la forma estándar hacemos referencia al formato en el que se deben expresar los polos y los ceros de la función para que sea posible obtener la información necesaria para la construcción del diagrama de Bode.
Utilizando el ejemplo de función de transferencia que utilizamos anteriormente, la forma estándar sería:
Esto quiere decir que los polos/ceros simples se expresan como:
Y los polos/ceros cuadráticos se expresan como
Para cambiar los polos y los ceros a su forma estándar se puede hacer la siguiente operación:
Y para los polos/ceros cuadráticos se utiliza:
Utilizando este concepto se puede convertir la función de transferencia que queremos graficar a su forma estándar:
Cuando se obtiene esta forma se procede remplazar las «s» por jω:
En la forma estándar es donde encontramos el valor de K, que para este caso es 10 (el valor que acompaña a «s» en el numerador) Con la forma estándar se procede a expresar la función de transferencia H en decibelios, utilizando para ello las propiedades de los logaritmos:
Con estas propiedades es posible reformar la función de transferencia de la siguiente manera:
En esta forma es importante reconocer el numerador y el denominador de la función de transferencia original: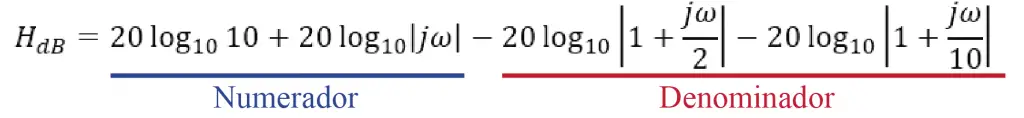
En esta forma es posible reconocer las asíntotas que tendrá el diagrama de Bode. Estas asíntotas marcarán la forma que tendrá el diagrama de Bode, pues en los diferentes tramos de este gráfico se observará un comportamiento equivalente a la suma de las asíntotas calculadas. Es por esta razón que es importante empezar dibujando las asíntotas y las frecuencias en las cuales se producen los cambios de pendiente en el diagrama de Bode (frecuencias de quiebre).
Trazado del diagrama de magnitud
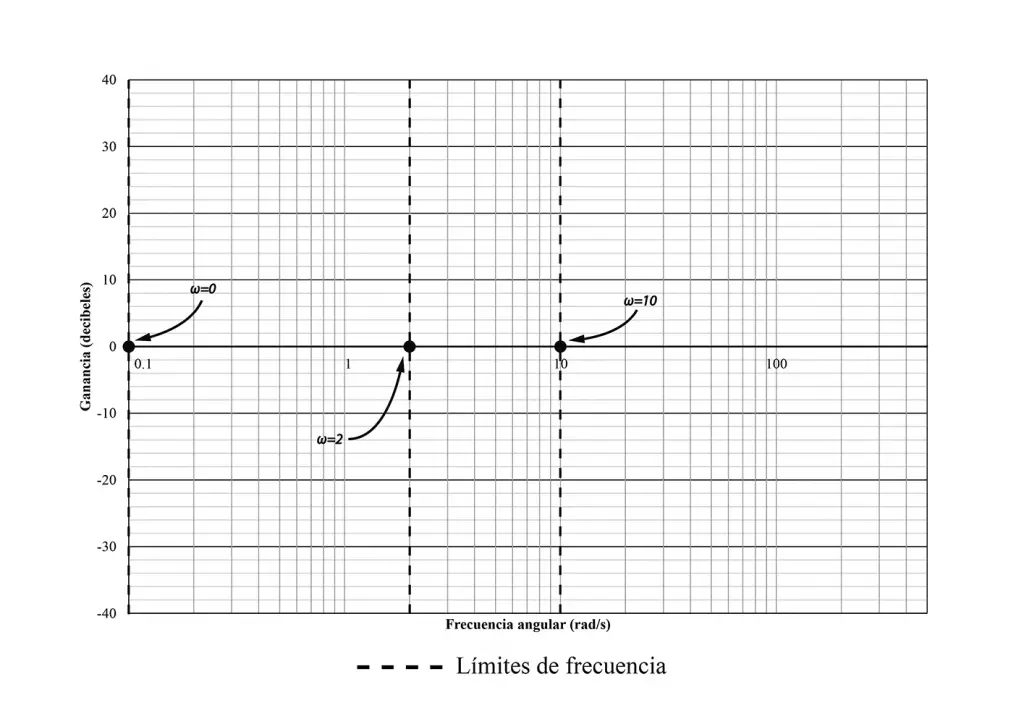
Para el diagrama de magnitud de Bode del ejemplo propuesto, se inicia marcando las frecuencias de quiebre en el eje horizontal. Estos límites se obtienen a partir de los polos y ceros (para este ejemplo, 0, 2 y 10).
En este enlace estoy dejando un archivo de Excel con una gráfica semilogarítmica configurable, tal como la que he usado para este ejemplo. Después de identificar las frecuencias límite en el plano semilogarítmico, se procede a dibujar las asíntotas. Para ello se recomienda utilizar como referencia la tabla de resumen de características de magnitud para los polos y los ceros.
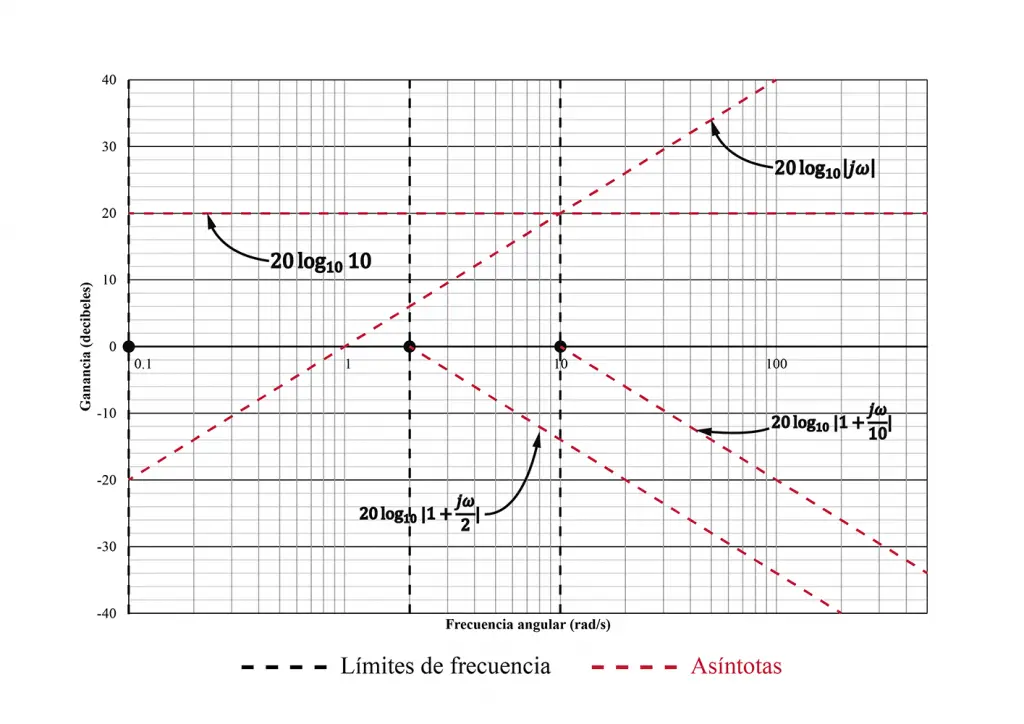
Las asíntotas, tal como refleja la tabla que compartimos más arriba en este documento, tienen pendientes de 0, 20 y 40 decibelios por década, positivas o negativas, dependiendo del tipo de elemento que las forma. Es importante utilizar la tabla de las pendientes para ubicar las asíntotas, tomando en cuenta los puntos en los cuales las asíntotas cortan el eje horizontal.
Por ejemplo, la asíntota producida por el cero en el origen tiene una pendiente de 20 decibles por década, y corta el eje horizontal en ω = 1, por lo que podemos deducir que en ω = 0, la línea se ubica en -20 dB. La K produce una asíntota de pendiente cero, que se ubica en 20log1010 que es igual a 20 dB. Los polos simples producen pendientes negativas de 20 decibelios por década que parten desde las frecuencias ω = 2 y ω = 10 (ver tabla de pendientes).
Con esta información se procede a hacer el diagrama de Bode. Hay una forma rápida y fácil de tener una idea de la ubicación de las líneas del diagrama: evaluando la expresión HdB en las frecuencias de quiebre.
Nótese que para ω = 0 se ha utilizado ω = 0.1, puesto no podemos calcular el logaritmo de 0. También resulta conveniente evaluar la frecuencia en una década posterior a la última frecuencia de quiebre, con el propósito de tener una idea hacia donde se dirige el gráfico conforme aumenta la frecuencia angular.
Hecho esto, se procede a marcar en el gráfico los puntos que han sido encontrados. Estos puntos nos darán una idea aproximada de la forma del gráfico, mas no necesariamente formarán parte de la aproximación asintótica. Esto se debe a que la aproximación asintótica es precisamente eso, una aproximación. Este paso es opcional, con el sólo propósito de tener una idea de la forma que tendrá el gráfico.
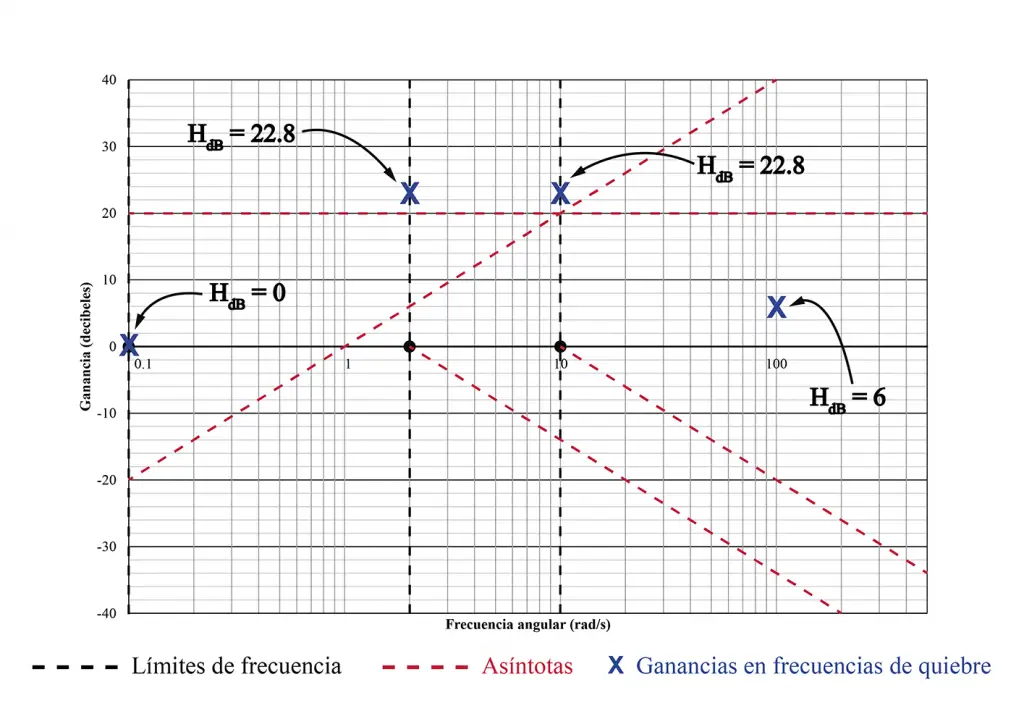
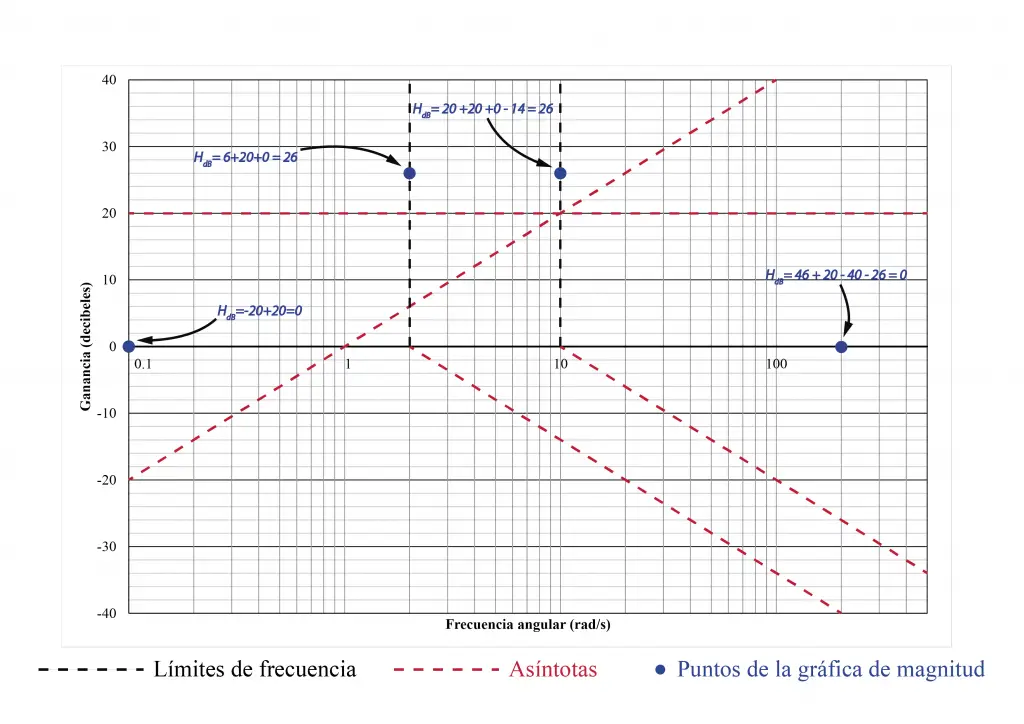
El gráfico de magnitud se obtendrá «sumando» las asíntotas en todos y cada uno de los intervalos de frecuencia. Es decir, el gráfico se forma a partir de la suma algebraica de los valores puntuales de cada una de las asíntotas. Para trazar el gráfico de manera precisa y rápida se recomienda sumar los valores de las asíntotas en cada uno de las frecuencias de quiebre.
Uniendo estos puntos se obtiene la aproximación asintótica. Como ya se ha mencionado, la aproximación asintótica se acercará al gráfico real, pero en alguno puntos, especialmente en los límites de frecuencia, los valores reales se desviarán un poco de la aproximación.
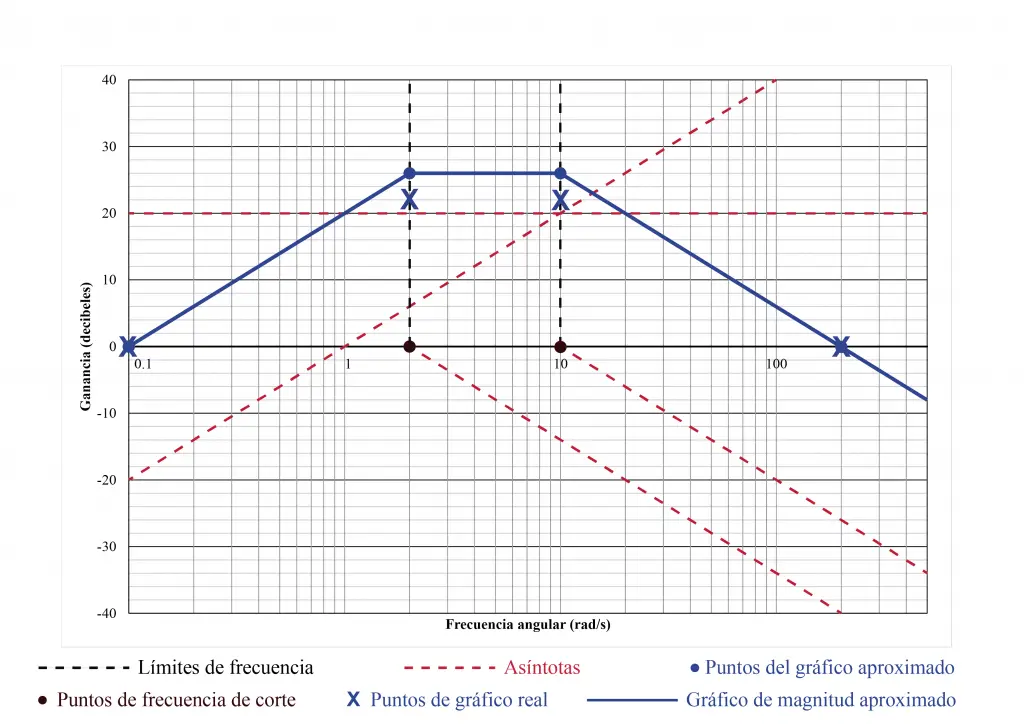 Una vez más debemos recalcar que el gráfico se construye con base en la suma de los valores puntuales de las asíntotas y no en los valores de ganancia calculados. En ω = 2 y ω = 10 la gráfica no coincide con las X, puesto que la pendiente de la asíntota del cero en el origen, que parte de cero y aumenta en 20 dB/década nos indica que el cruce con ω = 2 se produce aproximadamente en 26 dB, lo cual está por encima de los 22.8 dB de la ganancia «real».
Una vez más debemos recalcar que el gráfico se construye con base en la suma de los valores puntuales de las asíntotas y no en los valores de ganancia calculados. En ω = 2 y ω = 10 la gráfica no coincide con las X, puesto que la pendiente de la asíntota del cero en el origen, que parte de cero y aumenta en 20 dB/década nos indica que el cruce con ω = 2 se produce aproximadamente en 26 dB, lo cual está por encima de los 22.8 dB de la ganancia «real».
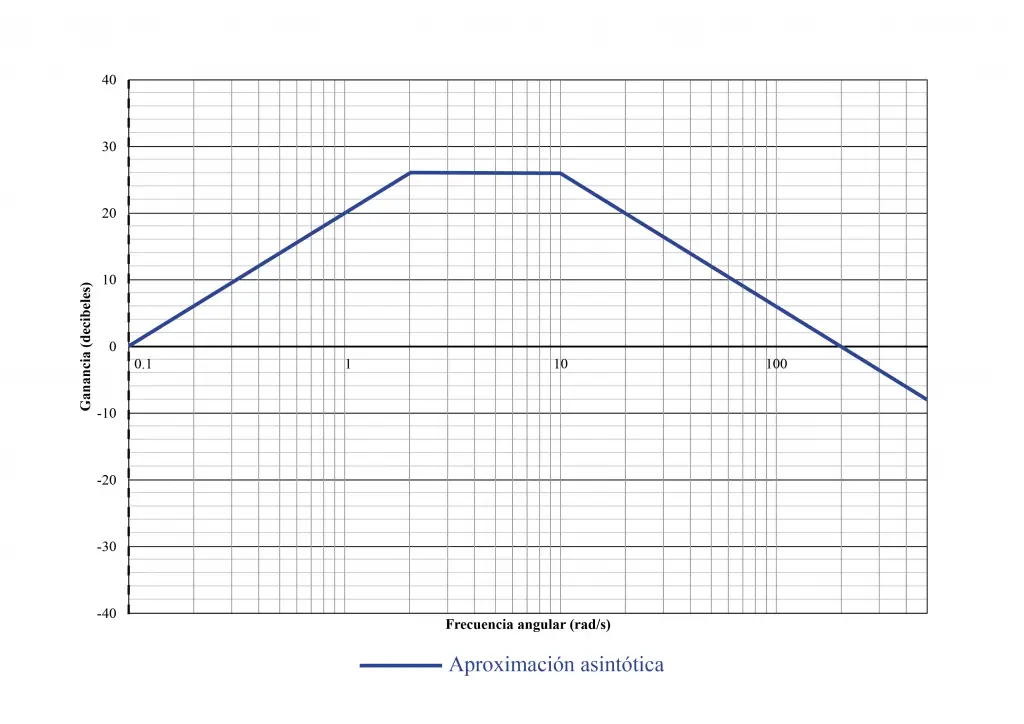
Llegado este punto se puede prescindir de las asíntotas y las marcas que se han colocado como referencia. Lo que nos interesa es la línea azul, el diagrama de magnitud de Bode.
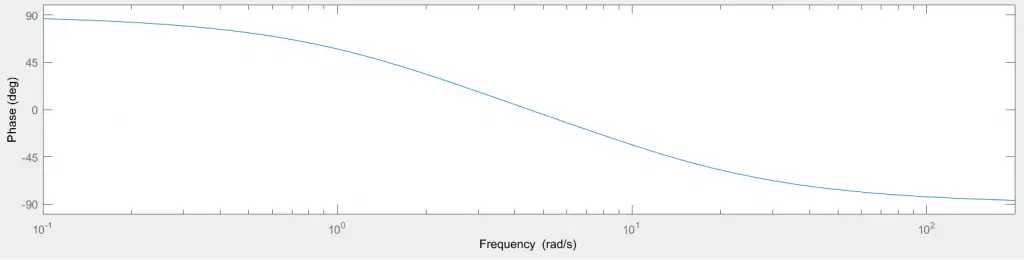
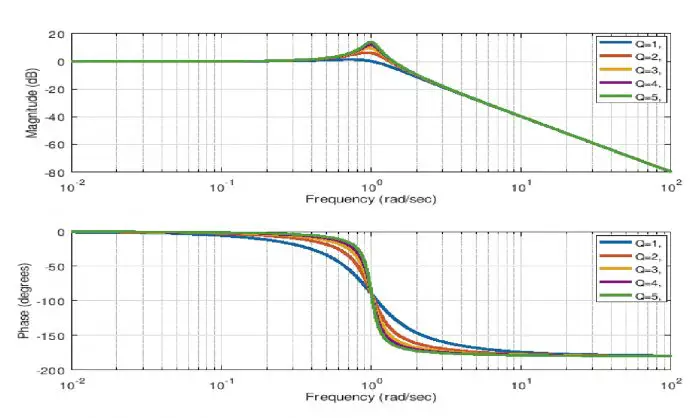
Utilizando Matlab es posible construir el gráfico real de Bode que parece a la aproximación asintótica, con la diferencia de que en las frecuencias de quiebre los cambios de pendiente no son tan bruscos como en la aproximación asintótica. El diagrama real presenta curvas suavizadas en comparación a las de la aproximación asintótica.
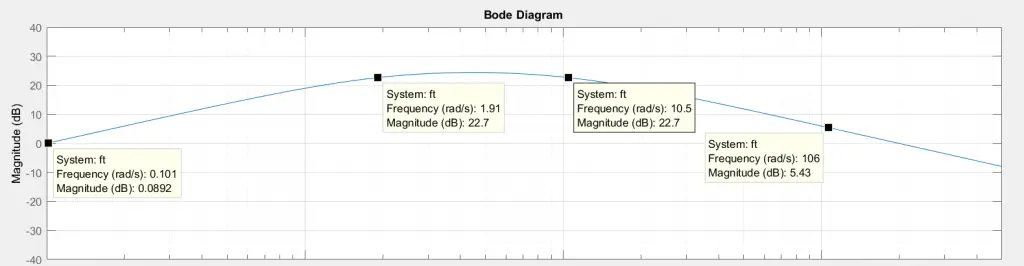
En la imagen se muestra el diagrama de Bode real producido por Matlab, donde se resaltan algunos puntos próximos a las frecuencias de corte. Estos se aproximan a los que calculamos anteriormente, por lo que podemos deducir que lo que hemos hecho hasta ahora es correcto.
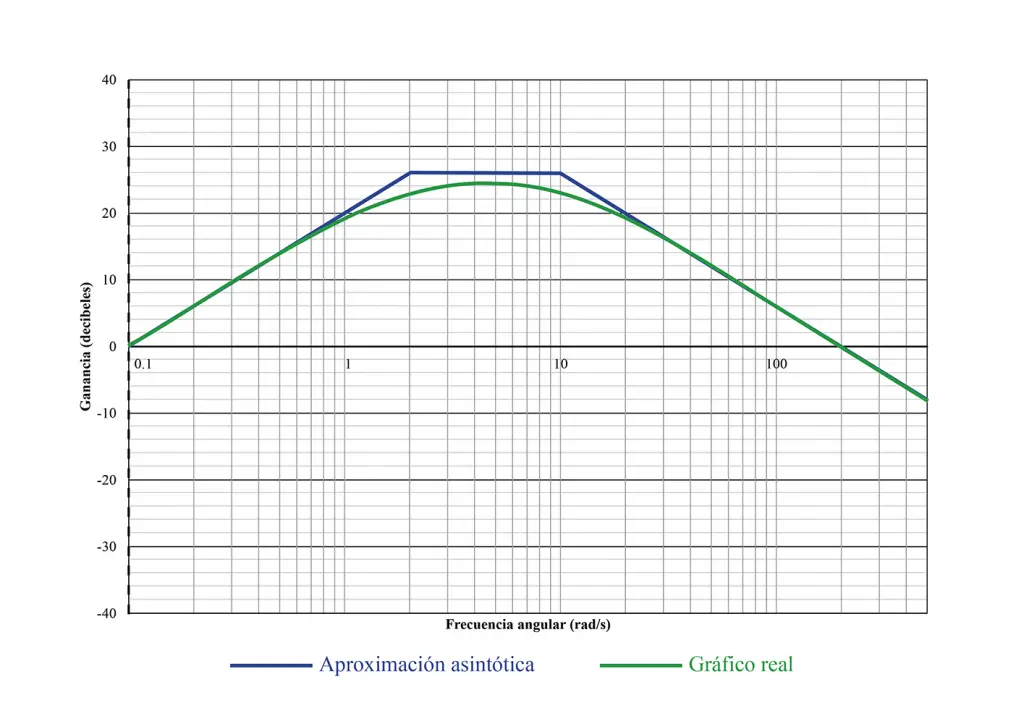
Me he tomado la tarea de superponer los dos gráficos, el que hemos construido con la aproximación y el que me ha generado Matlab.
La trayectoria del gráfico real si coincide con las X que habíamos colocado cuando estábamos construyendo la aproximación asintótica.
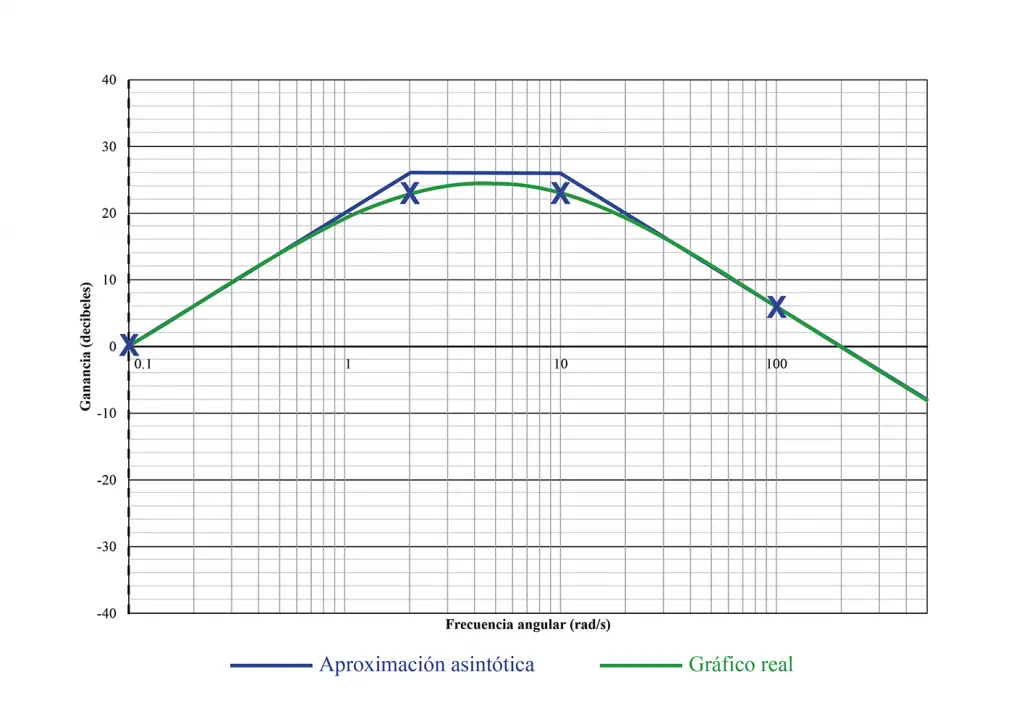
La aproximación asintótica nos da una idea clara de como es el gráfico real, con algunas imprecisiones en los cambios de pendiente, tal como se observa en la imagen anterior. Calculando la ganancia en las frecuencias próximas a una frecuencia de quiebre se puede aproximar la curva real, si lo que se desea es precisamente la curva real.
Trazado del diagrama de fase
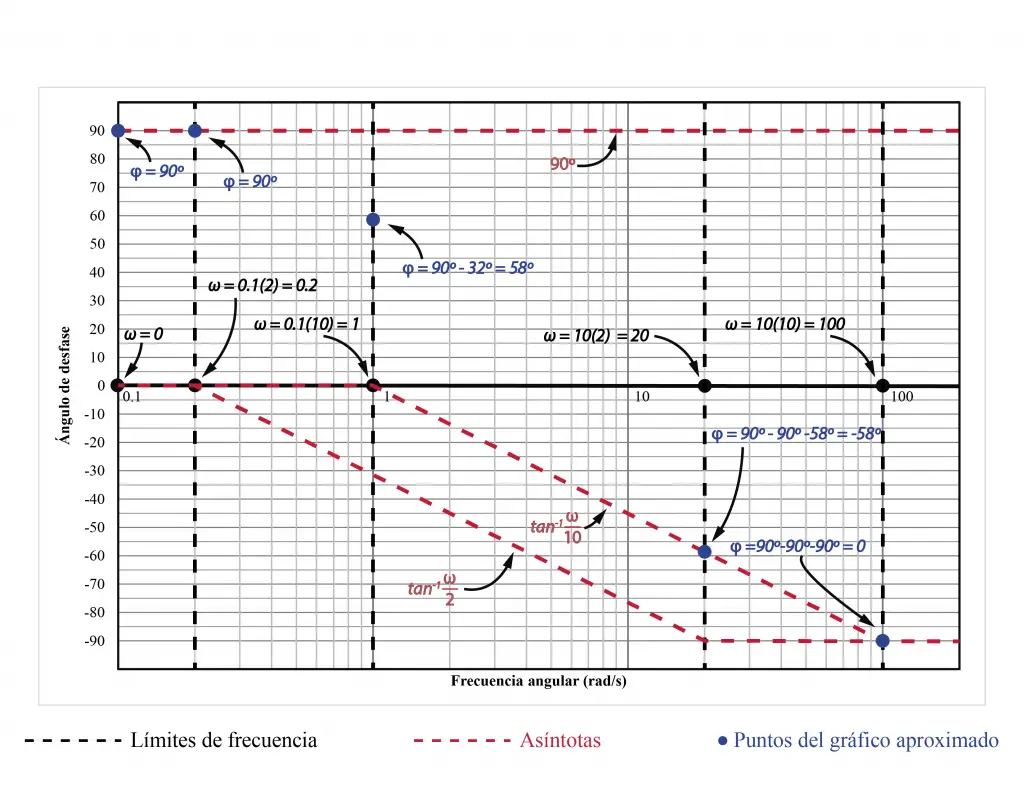
Para los diagramas de fase se sigue un procedimiento similar. Se marcan los valores de frecuencia importantes en el eje horizontal, se dibujan las asíntotas y se buscan los valores de ángulos de desfase en las frecuencias de quiebre, utilizando los valores puntuales de las asíntotas.
Al unir los puntos azules, del gráfico aproximado, se obtiene el diagrama de Bode de fase.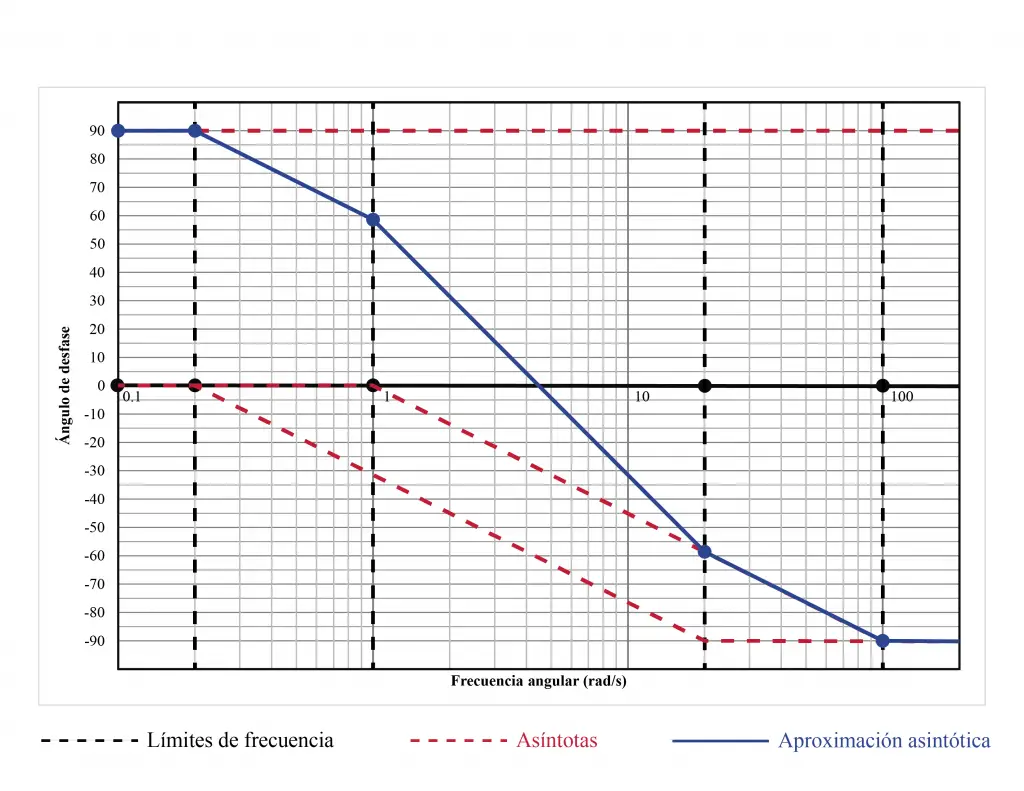 Este diagrama se parece mucho al diagrama real que nos proporciona Matlab.
Este diagrama se parece mucho al diagrama real que nos proporciona Matlab.
Me he tomado la tarea de superponer el gráfico producido en Matlab con la aproximación asintótica. El gráfico real se acerca bastante a la aproximación asintótica y coincide con los valores de desfase que he calculado en las frecuencias de quiebre y que he marcado con las X azules.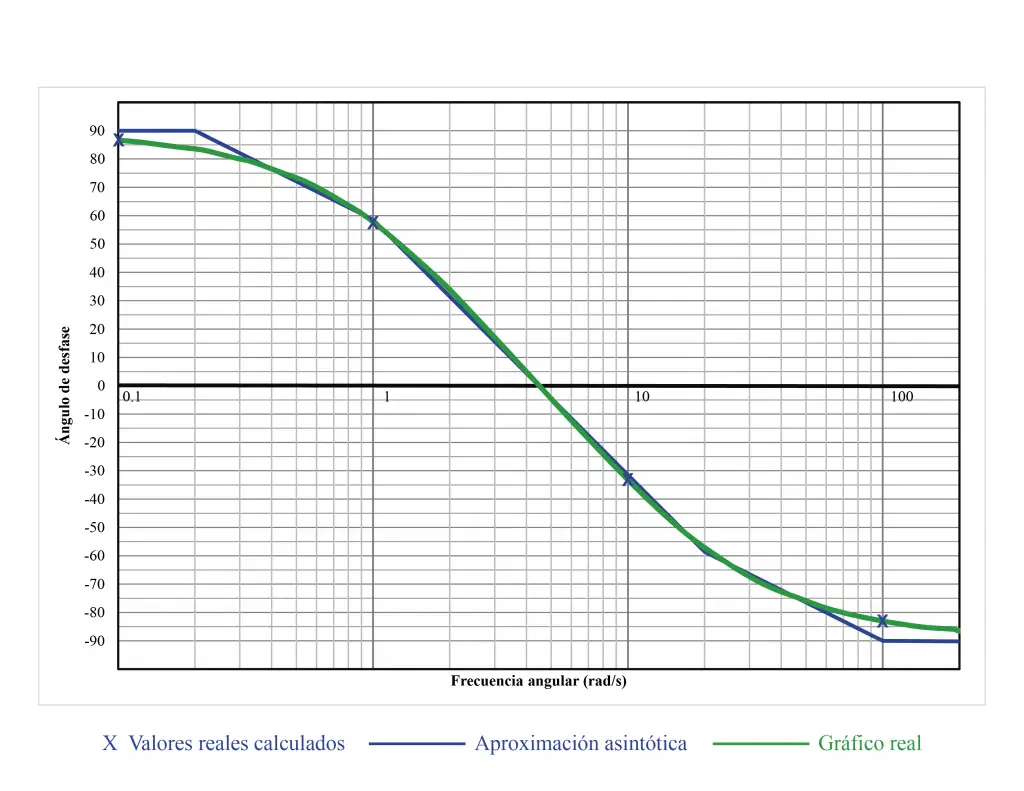
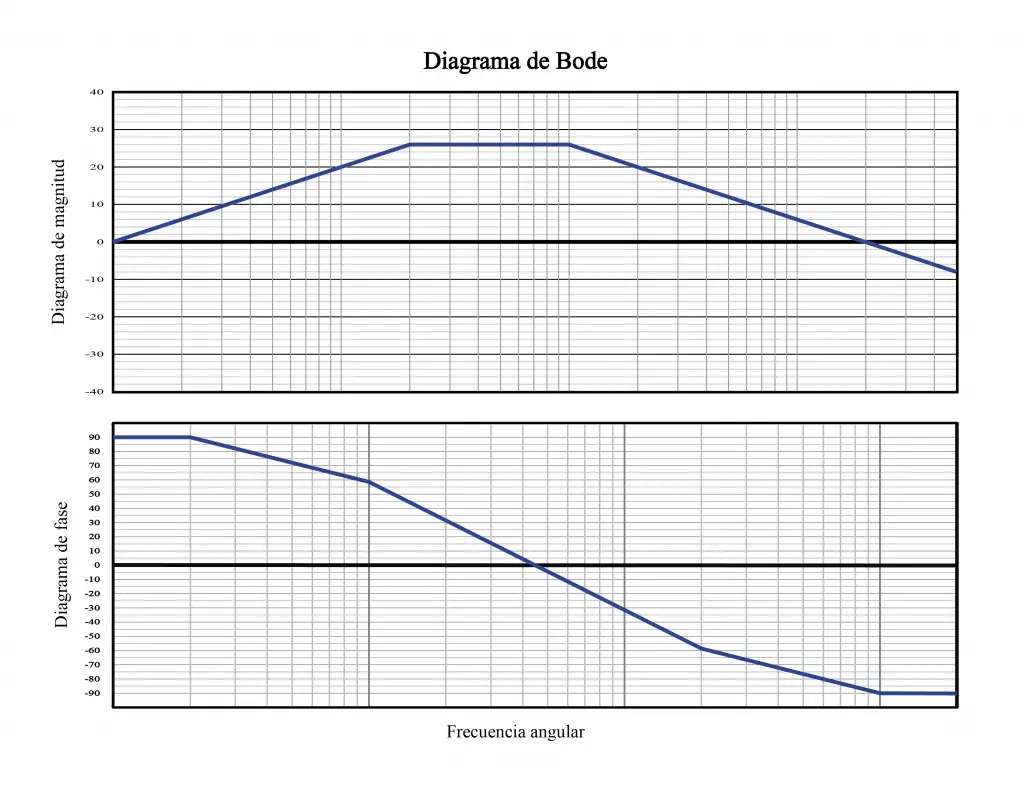
Finalmente, ahora que tenemos los gráficos de Bode de magnitud y fase, podemos armar nuestro diagrama de Bode completo.
Y aquí tenemos el diagrama de Bode completo.
Conclusión
En este post, se ha explicado qué son los diagramas de Bode y cómo se utilizan para representar gráficamente el comportamiento de un sistema a diferentes frecuencias. Se ha explicado que un diagrama de Bode se compone de dos gráficas: una de magnitud o ganancia, que representa la relación entre la amplitud de la señal de salida y la de entrada a cada frecuencia, y otra de fase, que representa el desfase entre ambas señales a cada frecuencia.
También se ha explicado cómo construir un diagrama de Bode a partir de una función de transferencia dada. Se ha mostrado cómo factorizar la función para identificar los polos y ceros de la función, cómo convertir la función a su forma estándar y cómo calcular las asíntotas del diagrama de magnitud y la fase para cada frecuencia.
Esperamos que hayas encontrado este post sobre los diagramas de Bode útil y hayas aprendido algo nuevo sobre esta herramienta tan importante en ingeniería eléctrica y electrónica. Si tienes alguna pregunta o comentario sobre este tema, no dudes en dejarnos un mensaje en la sección de comentarios. Estaremos encantados de leer tus comentarios y ayudarte con cualquier duda que puedas tener. ¡Gracias por leer!

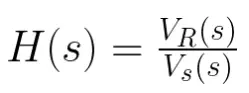
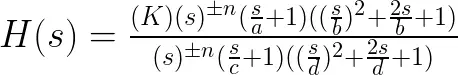
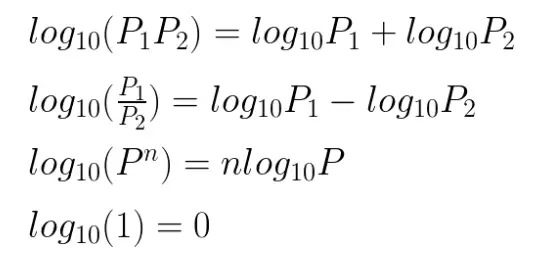
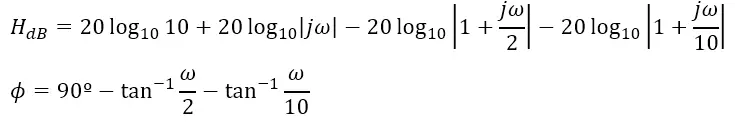
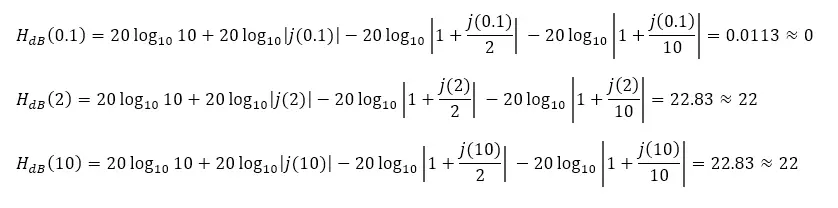
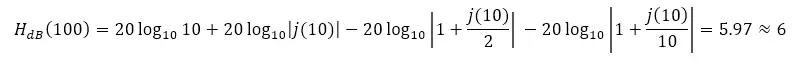








Excelente trabajo
Gracias por el enlace que me lleva a un archivo en excel
que permite el trazado manual de los diagramas asintoticos de bode.
Buena chavales. Aviso la información esta exquisita, muy completa!!. Pero por favor aclaren que a la hora de sacar la ganancia de cada polo y cero se debe primero obtener su modulo y después aplicarle el logaritmo.
Ej;
4+5wj
Módulo: 20log[√(4^²+(5w)^²)]
ACLARACION; Los cálculos tan bien, era eso lo que quería resaltar. Espero que sea útil mi acotación. Desde ya muchas gracias por la explicación. ???
Gracias a ti por el aporte.
Saludos.
woooo, gracias en verdad