El programa de televisión Let’s Make a Deal presenta un problema de probabilidad que ha sido ampliamente discutido a nivel del mundo. Let’s Make a Deal es un programa que fue lanzado originalmente en 1963 y que sigue siendo transmitido en la actualidad. El programa consiste en una serie de juegos en los que se le ofrecen premios a los participantes que son escogidos del público. La dinámica es dirigida por un «host» que se encarga de ofrecerles «deals» a los participantes. Dependiendo de las decisiones de estos, se podrían llevar grandes premios o perderlo todo.
En 1975 el profesor de estadística Steve Selvin envió una carta al journal American Statician en el que proponía un problema y su posible solución. Este problema ha pasado a llamarse «Monty Hall Problem» debido a que el problema se basaba en uno de los juegos del programa, cuyo presentador era Monty Hall en aquellos años.
El problema consiste en lo siguiente:
Supongamos que te invitan a un programa de televisión en el que te ofrecen escoger una de tres puertas, tras las cuales hay un premio. Detrás de una de las puertas hay un automóvil y en las otras dos habrá una cabra en cada una. Tú escoges una de las puertas y el presentador del programa, que sabe donde esta el premio, elimina una de las dos puertas que no escogiste y procede a ofrecerte un trato: puedes cambiar la puerta que escogiste en un principio o mantenerte en tu decisión original. ¿Cuál es la mejor opción para el jugador?
Este problema se volvió famoso luego de que en 1990 un lector leenvió una carta a Marilyn vos Savant, quien escribía la columna «Ask Marilyn» (preguntale a Marilyn) en la revista Parade. Para quienes no la conocen, Marilyn vos Savant es la mujer que apareció en el libro de los Record Guiness como el coeficiente intelectual más alto entre 1986 y 1989.
Desde 1986, vos Savant tiene la columna «Ask Marilyn» en la que contesta preguntas a sus lectores. Una de estas preguntas fue la del problema Monty Hall, a lo cual ella respondió que «la mejor opción es escoger una puerta y luego cambiar esa puerta por otra, pues esto te da una probabilidad de un 66% de escoger la puerta con el automóvil».
Esta afirmación provocó que miles de lectores de la revista Parade escribieran diciéndole a vos Savant que estaba equivocada. Ella hizo una demostración y la publicó en la siguiente edición de la revista, lo cual causó aún más controversia, pues los lectores no estaban de acuerdo con la respuesta. La noticia sobre el debate alrededor de este problema fue publicada incluso en la página frontal del New York Times.
Lo cierto es que vos Savant tenía razón. La probabilidad de ganar el juego, es decir, escoger la puerta tras la cual se encuentra el vehículo es mayor si se escoge una opción y luego esta se cambia por otra opción. Esto ha sido demostrado matemáticamente y por medio de simulaciones computacionales y experimentos con personas.
El día de hoy traigo para ustedes una simulación en Java con la cual se hacen experimentos en los que la computadora escoge las respuestas al azar. El código se encuentra disponible en nuestro repositorio de Github.
Antes de proceder con la confección de este programa se hizo una prueba de verificación a la clase Random de Java. Se confeccionó un algoritmo que produce números entre , 2 y 3 unas 100 000 veces. Si la clase Random produce números aleatorios sin seguir un patrón definido, la probabilidad de obtener un 1, un 2 o un 3 es igual, es decir, aproximadamente 33.3% para cada uno.
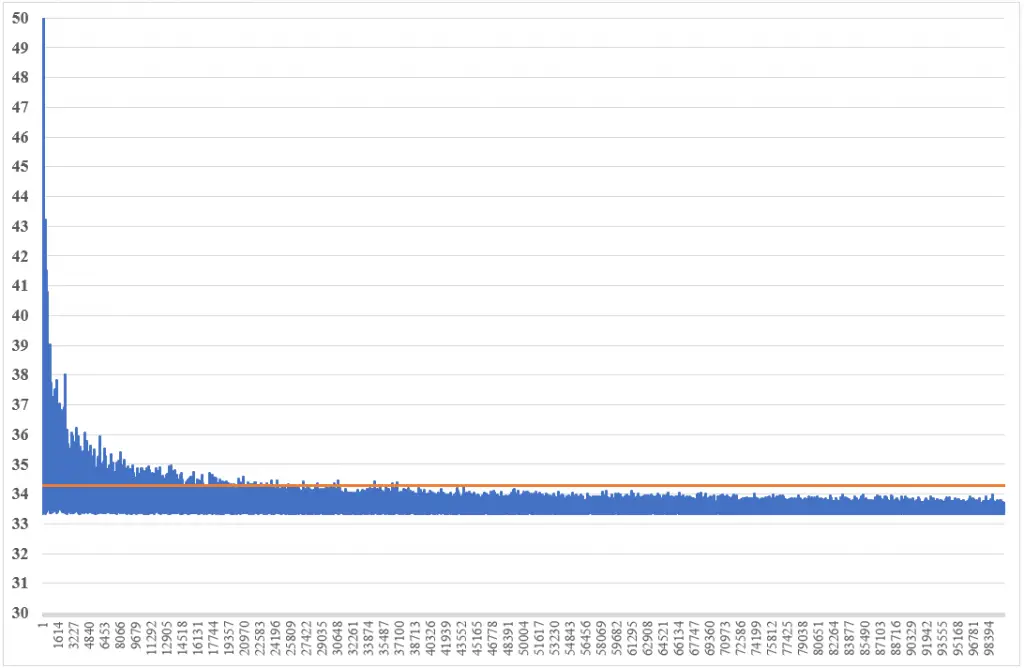
El gráfico muestra que después de 45 000 iteraciones los porcentajes máximos obtenidos son menores a 34.3%, por lo que se puede decir que de 50 000 iteraciones en adelante se producen resultados bastante consistentes. A partir de este punto las se obtienen más o menos la misma cantidad de las cifras 1, 2 o 3 producidas aleatoriamente.
Para comprobar el experimento del problema de Monty Hall deberíamos ejecutar más de 50 000 iteraciones para obtener resultados más precisos. Se ha creado una interfaz gráfica muy sencilla que permite simular una determinada cantidad de iteraciones. Es posible establecer distintas condiciones en cuanto a las decisiones del jugador, de forma tal que se pueden evaluar múltiples casos de estudio. El programa ejecutable se puede descargar desde este enlace.

Al ejecutar el experimento se verifican algunas cosas:
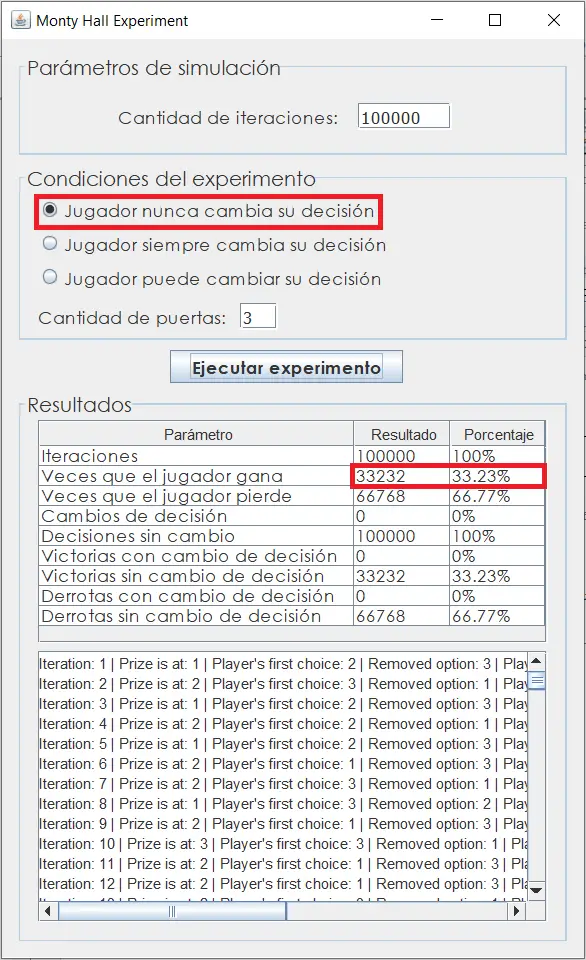
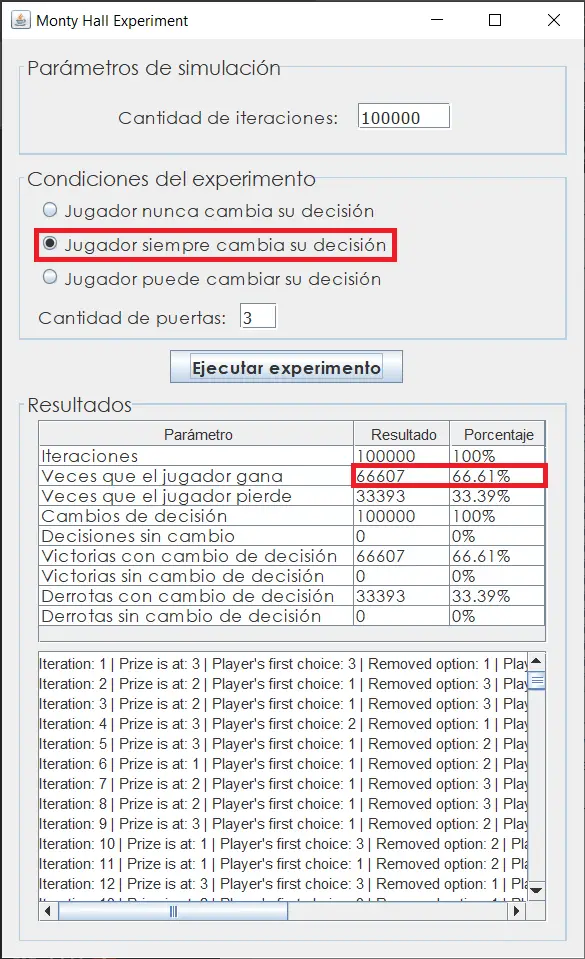
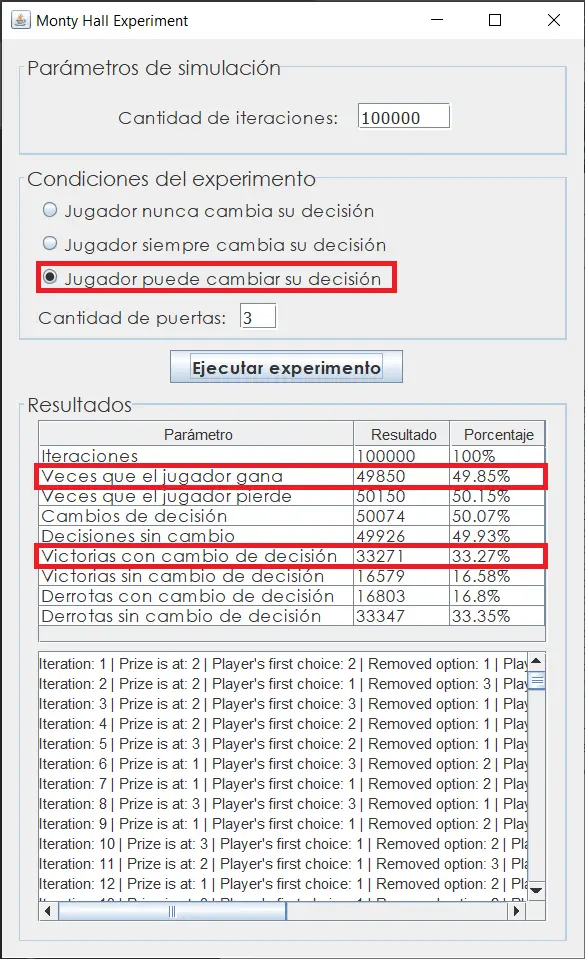
Tu puedes descargar el programa y hacer tus propias simulaciones. Ha quedado comprobado que, aunque parezca ilógico, la mejor oportunidad de ganar en este juego es escoger una de las 3 puertas, esperar a que el host del programa elimine una de las puertas y luego cambiar la opción que escogiste inicialmente por aquella que el host no descartó. Nunca se tendrá el 100% de certeza sobre un fenómeno de este tipo, pero 66% es mucho más que el 33% de probabilidad de ganar que tienes si no cambias de decisión.