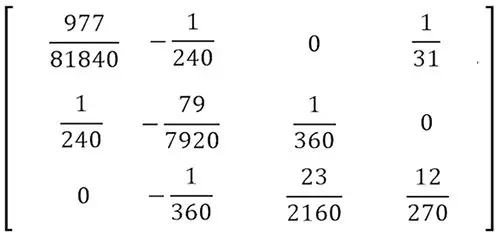Este artículo pretende presentar una opción para resolver sistemas de Ecuaciones de Kirchhoff con Excel, una herramienta muy útil dado que en casi todas las computadoras está instalada. Siempre es para mí una sorpresa que los 2 posts más visitados en Panama Hitek están relacionados a las Leyes de Kirchhoff. Ambos contenidos se encuentran disponibles en los siguientes enlaces:
- Ley de las corrientes de Kirchhoff: Método de nodos
- Ley de los voltajes de Kirchhoff: Método de Mallas
En ambos posts hemos analizado el mismo circuito, el cual presentamos a continuación.


Ambos esquemas han sido resueltos paso a paso en los posts que hemos enlazado en este artículo. Al analizar estos circuitos, encontramos 2 sistemas de ecuaciones, uno con sumatoria de voltajes y el otro con sumatoria de corrientes.


En ambos contenidos muestro diferentes métodos para resolver los sistemas de ecuaciones que resultan del análisis de cada circuito.
Recientemente mi amigo Secundino Villarreal, Ingeniero Electromecánico y docente de Física en la Universidad Tecnológica de Panamá ha lanzado un blog orientado a la publicación de plantillas en Excel. El sitio se llama http://excelparaingenieria.com, el cual recomiendo visitar. El Ing. Secundino publicó una plantilla sobre el método de Gauss-Jordan, el cual puede ser utilizado para despejar incógnitas en sistemas de ecuaciones lineales. Las ecuaciones de Kirchhoff, sea sumatoria de corrientes o de voltajes obdecen comportamientos lineales, por lo cual es posible utilizar estas plantillas para encontrar nuestras incógnitas, lo cual explicaremos en breve.
Sistema de ecuaciones con sumatoria de voltajes
El sistema de ecuaciones del ejemplo de mallas es un sistema de 4 ecuaciones con 4 incógnitas. Para resolverlo podemos utilizar la plantilla titulada Gauss Jordan: Ecuaciones Simultáneas 4 x 4, la cual podemos descargar de forma gratuita desde el enlace proporcionado.
Cuando la descargamos veremos algo como esto:
Un poco más abajo encontraremos un cuadro donde ingresamos los valores de nuestras ecuaciones. La plantilla irá calculando automáticamente las respuestas del problema al hacer la reducción de Gauss-Jordan.
Los valores de las corrientes que balancean el sistema de ecuaciones serán los valores de corriente en cada malla. El usuario puede escoger la forma como desea que los datos queden visualizados, ya sea en notación científica, fracciones, decimales, etc. Como ya dijimos, la plantilla la podemos descargar desde la web del autor.
Sistema de ecuaciones con sumatoria de Corrientes
Para facilitar las cosas con Excel, es recomendable que reduzcamos la matriz a valores de fraccionarios, realizando las sumas que quedaron implícitas en nuestra matriz de ecuaciones. De esta manera nos debe quedar una matriz como esta:
También podemos transformar estas fracciones a decimales.
Una vez tengamos estos datos, es muy fácil resolver este sistema de ecuaciones utilizando Excel.
Para este caso hemos utilizado la plantilla Gauss Jordan: Ecuaciones Simultáneas 3 x 3 para resolver el sistema de ecuaciones de este ejemplo. La plantilla se encuentra disponible de forma gratuita en la web del autor. Cuando la descargamos veremos algo como esto:
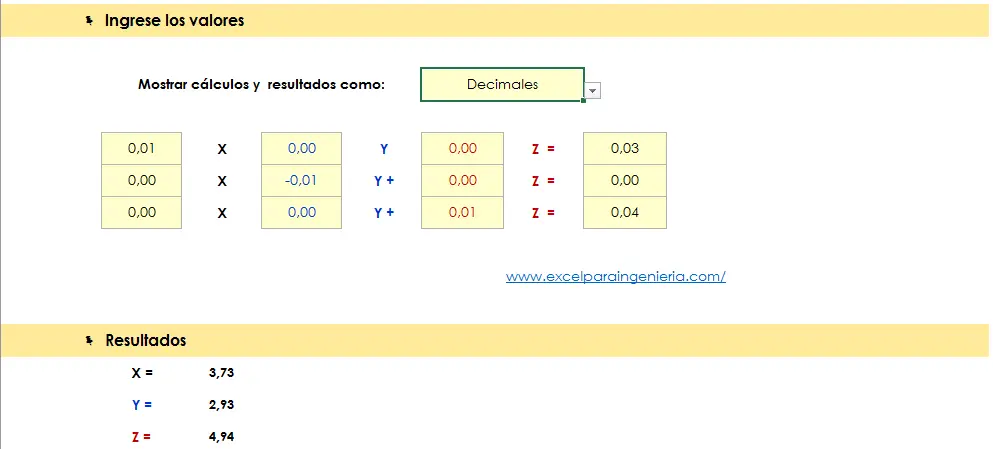
Un poco más abajo encontraremos un cuadro donde ingresamos los valores de nuestras ecuaciones. La plantilla irá calculando automáticamente las respuestas del problema al hacer la reducción de Gauss-Jordan.
Los valores de los voltajes que balancean el sistema de ecuaciones serán los valores de voltajes en cada nodo. En la matriz solo vemos números con dos decimales, debido a que ésta es la cantidad preestablecida por el diseñador. El usuario puede escoger la forma como desea que los datos queden visualizados, ya sea en notación científica, fracciones, decimales, etc. Como ya dijimos, la plantilla la podemos descargar desde la web del autor.
Existen múltiples formas de resolver un sistema de ecuaciones lineales. Esta es, simplemente, una opción más que los usuarios pueden utilizar para el paso final en este tipo de problemas. Esperamos que la información presentada sea útil para ustedes. Saludos.