El otro día estaba analizando unos datos de un analizador de calidad de energía eléctrica y se me presentó una situación interesante que me llevó a tener que pensar un poco «out of the box». Por alguna razón que desconozco el equipo no registró los voltajes entre líneas en un sistema trifásico conectado en estrella. Sin embargo, el equipo sí registró los voltajes de fase y sus ángulos de fase correspondientes y con esta información es posible calcular los voltajes de línea a línea.
Lo lógico, para la mayoría, sería multiplicar los voltajes de fase por √3. Pero cuando te pones a pensar en este tema te das cuenta que eso solo funciona para sistemas balanceados, con una diferencia en los angulos de fase de 120º. En un sistema real esta condición difícilmente se cumple, tal como demostraré en este aporte.
Decidido a calcular un modelo que me permitiera calcular el voltaje de línea a partir de un voltaje de fase, considerando los ángulos de desfase, llegué a la siguiente expresión:
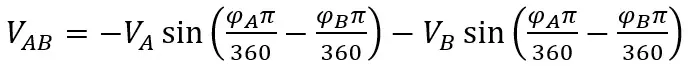 En esta ecuación VA y VB son las amplitudes de las fases cuyo voltaje se quiere calcular y φA y φB son sus respectivos ángulos de fase, dados en grados.
En esta ecuación VA y VB son las amplitudes de las fases cuyo voltaje se quiere calcular y φA y φB son sus respectivos ángulos de fase, dados en grados.
En el siguiente escrito voy a explicar el razonamiento que utilicé para llegar a esta expresión y demostraré el correcto funcionamiento de este modelo. Espero les sea de utilidad.
Planteamiento del problema
En un sistema trifásico de potencia, una conexión en estrella luce de la siguiente manera:
 En este tipo de sistemas, a los voltajes referidos al neutro (representados en color rojo) se les conoce como voltajes de fase. A los voltajes entre las fases (o líneas) se les conoce como voltajes de línea a línea, o simplemente voltajes de línea.
En este tipo de sistemas, a los voltajes referidos al neutro (representados en color rojo) se les conoce como voltajes de fase. A los voltajes entre las fases (o líneas) se les conoce como voltajes de línea a línea, o simplemente voltajes de línea.
Idealmente en un sistema balanceado existe una diferencia de fase entre VAN, VBN y VCN de 120º. Si tomamos en cuenta un sistema con voltajes de fase de 120 voltios, los voltajes de línea serían:
 Para hacer estos cálculos nos hemos apoyado en un simulador de una calculadora programable (Ti-Nspire CX CAS). Hemos representado los voltajes de fase (va, vb y vc) en su forma fasorial. Al calcular la diferencia de potencial entre VA y VC vemos que la magnitud es √3·120, es decir, la magnitud del voltaje de fase multiplicada por √3. Cada voltaje de línea se encuentra desfasado 30º con respecto al voltaje de fase, pero por ahora no nos importa mucho este desfase. La magnitud es lo que nos interesa.
Para hacer estos cálculos nos hemos apoyado en un simulador de una calculadora programable (Ti-Nspire CX CAS). Hemos representado los voltajes de fase (va, vb y vc) en su forma fasorial. Al calcular la diferencia de potencial entre VA y VC vemos que la magnitud es √3·120, es decir, la magnitud del voltaje de fase multiplicada por √3. Cada voltaje de línea se encuentra desfasado 30º con respecto al voltaje de fase, pero por ahora no nos importa mucho este desfase. La magnitud es lo que nos interesa.
Sin embargo, esto solo es válido si el sistema está balanceado. Por ejemplo, ¿qué tal si en una fase tenemos 120 voltios y en la otra fase tenemos 115 voltios?
 Si verificamos este resultado contra la utilización del √3 vemos que este valor ya no nos es útil para calcular la magnitud del voltaje de línea:
Si verificamos este resultado contra la utilización del √3 vemos que este valor ya no nos es útil para calcular la magnitud del voltaje de línea:
 Es decir, cuando utilizamos la forma fasorial de VA y VB obtenemos la magnitud de la diferencia de potencial entre VA y VB. Pero si multiplicamos las magnitudes por √3 no lograremos obtener el resultado esperado.
Es decir, cuando utilizamos la forma fasorial de VA y VB obtenemos la magnitud de la diferencia de potencial entre VA y VB. Pero si multiplicamos las magnitudes por √3 no lograremos obtener el resultado esperado.
Lo mismo sucede si el desfase entre VA y VB es distinto de 120º:
En conclusión, para calcular una diferencia de potencial entre dos fases que no estén desfasadas 120º entre sí hace falta hacer el cálculo utilizando la forma fasorial de los voltajes de fase, tomando en cuenta tanto la magnitud como la fase.
Análisis en el dominio del tiempo
Calcular la diferencia de potencial entre dos fases utilizando la forma fasorial del voltaje está bien, pero no siempre contamos con una calculadora con capacidad de hacer operaciones con números complejos. O a veces simplemente no es tan sencillo trabajar con números reales e imaginarios.
Por esta razón me propuse encontrar una expresión que facilitara el cálculo de la magnitud del voltaje de línea en función del desfase de los ángulos de fase. Para esto hace falta entender que representan las magnitudes de las que estamos hablando.
Si deseamos modelar los voltajes de fase en el dominio del tiempo, tendríamos las siguientes expresiones.
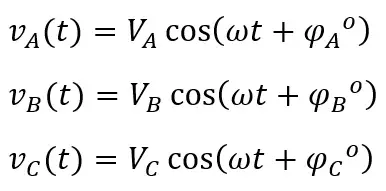 En este modelo VA, VB y VC son las amplitudes máximas de cada voltaje de fase. Los ángulos de fase serán φA, φA y φc,mientras que ω es la frecuencia angular de la red, la cual se calcula a partir de la frecuencia en Hertz (ω=2πf).
En este modelo VA, VB y VC son las amplitudes máximas de cada voltaje de fase. Los ángulos de fase serán φA, φA y φc,mientras que ω es la frecuencia angular de la red, la cual se calcula a partir de la frecuencia en Hertz (ω=2πf).
Un sistema trifásico, 120 voltios, 60 hz, luce de la siguiente manera:
 De forma similar podemos graficar el voltaje de línea a línea, por ejemplo vAB(t) si combinamos los modelos de vA(t) y vB(t):
De forma similar podemos graficar el voltaje de línea a línea, por ejemplo vAB(t) si combinamos los modelos de vA(t) y vB(t):
La gráfica de este modelo luce de la siguiente manera:
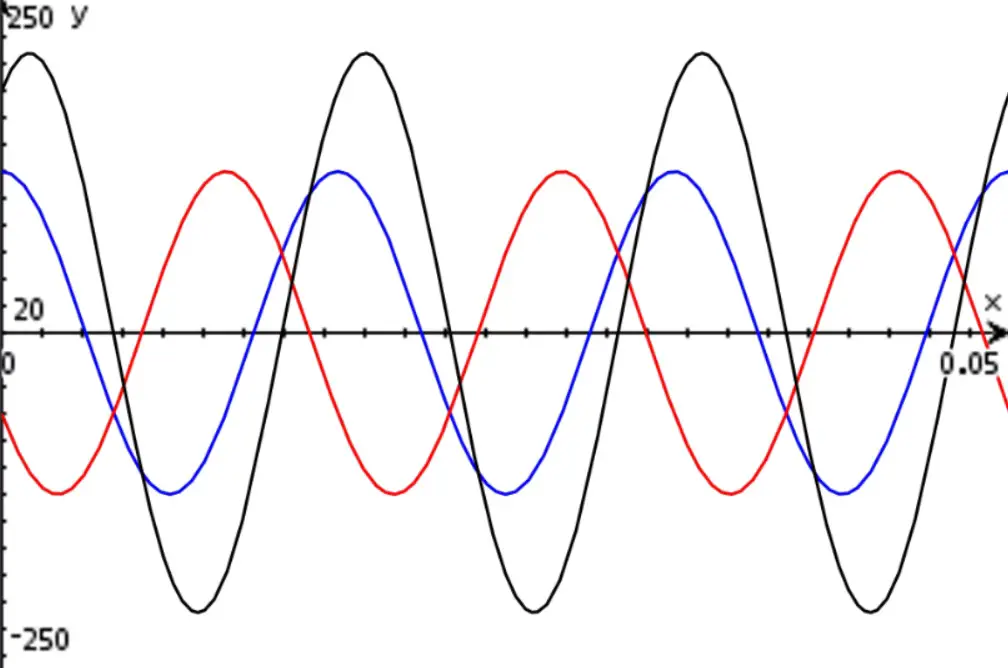 Utilizando las herramientas de análisis de la computadora, podemos obtener los máximos y los mínimos de este gráfico:
Utilizando las herramientas de análisis de la computadora, podemos obtener los máximos y los mínimos de este gráfico:
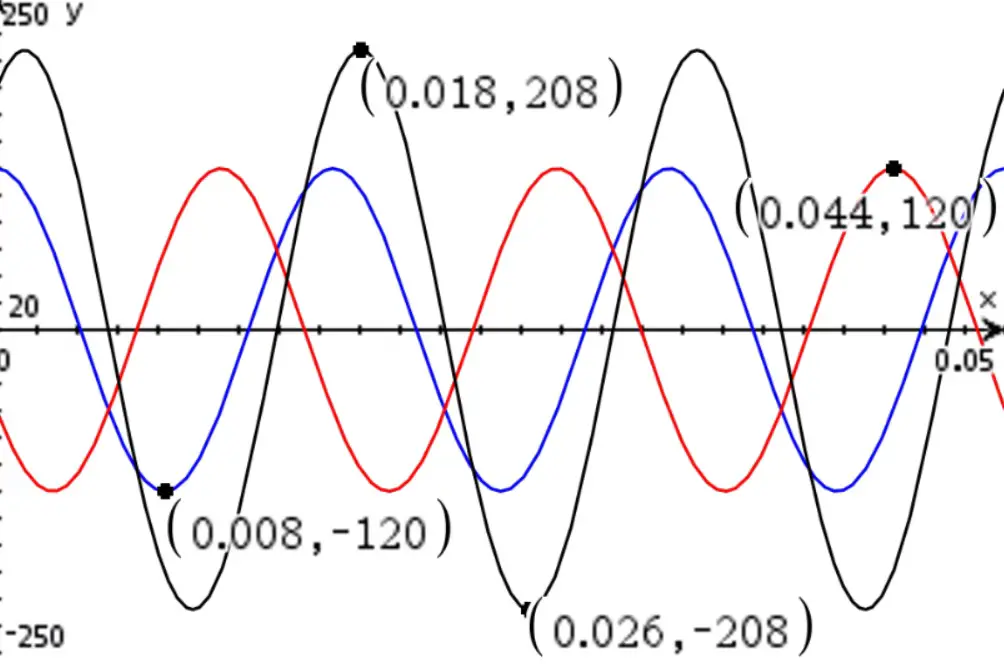 El 208 es el valor correspondiente a 120·√3. Si cambiamos la amplitud de la fase B, como hicimos anteriormente, por 115 voltios, veremos:
El 208 es el valor correspondiente a 120·√3. Si cambiamos la amplitud de la fase B, como hicimos anteriormente, por 115 voltios, veremos:
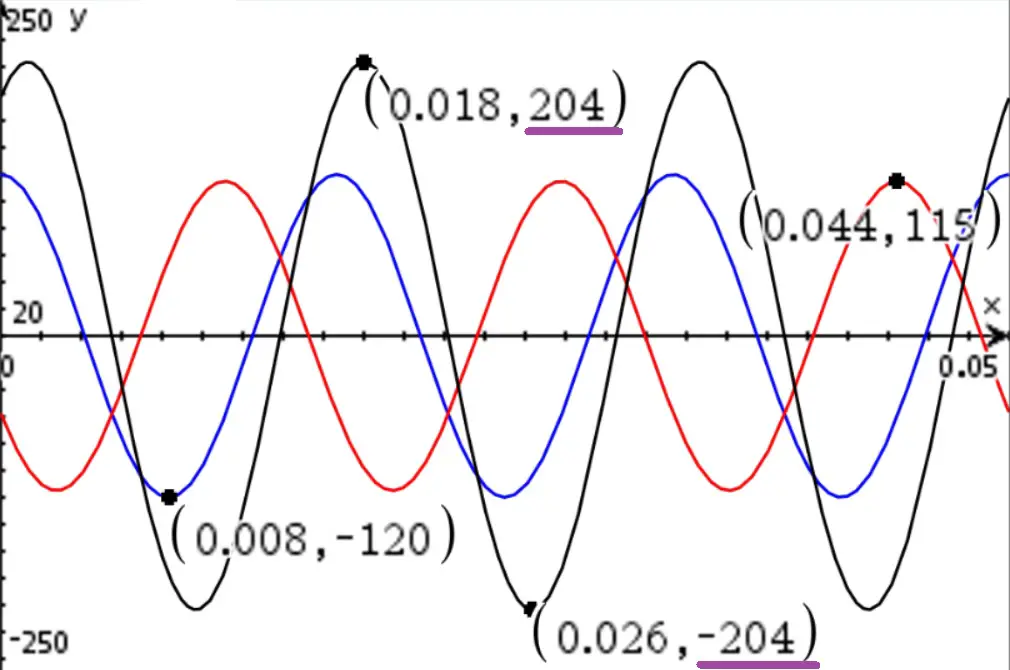 Este valor, 204, ya lo habíamos obtenido antes cuando calculamos el diferencial entre VA y VB usando fasores (en realidad fue 203.53, solo que aparece redondeado). Si hacemos la prueba del desfase de 118 grados, tendremos:
Este valor, 204, ya lo habíamos obtenido antes cuando calculamos el diferencial entre VA y VB usando fasores (en realidad fue 203.53, solo que aparece redondeado). Si hacemos la prueba del desfase de 118 grados, tendremos:
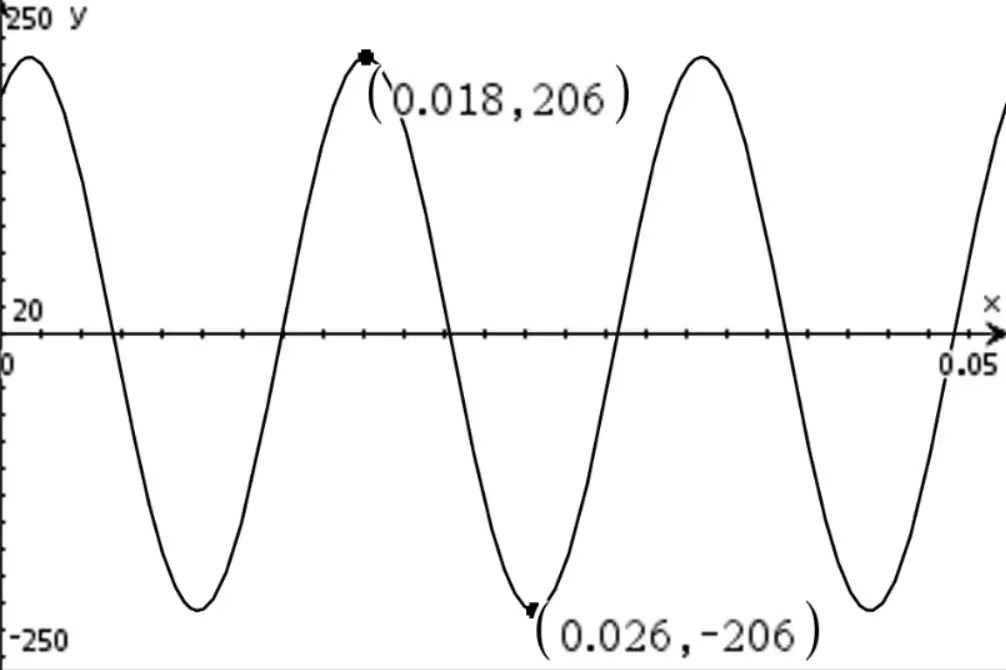 Una vez más obtenemos el valor esperado (205.72 redondeado). Esto permite concluir que para calcular la amplitud del voltaje de línea cuando el desfase es distinto de 120º se debe utilizar el modelo matemático de vAB(t) evaluado en el tiempo en el que alcanza su valor máximo o mínimo.
Una vez más obtenemos el valor esperado (205.72 redondeado). Esto permite concluir que para calcular la amplitud del voltaje de línea cuando el desfase es distinto de 120º se debe utilizar el modelo matemático de vAB(t) evaluado en el tiempo en el que alcanza su valor máximo o mínimo.
Como vAB(t) es una función diferenciable en el intervalo 0≥t≥∞, podemos utilizar la derivada para encontrar el tiempo en el que esta función alcanza su valor máximo.
Por definición, la derivada de una función representa la pendiente de la recta tangente a una curva. Si analizamos la curva vAB(t) podemos verificar gráficamente que en los máximos y mínimos de la función la recta tangente es igual a cero:
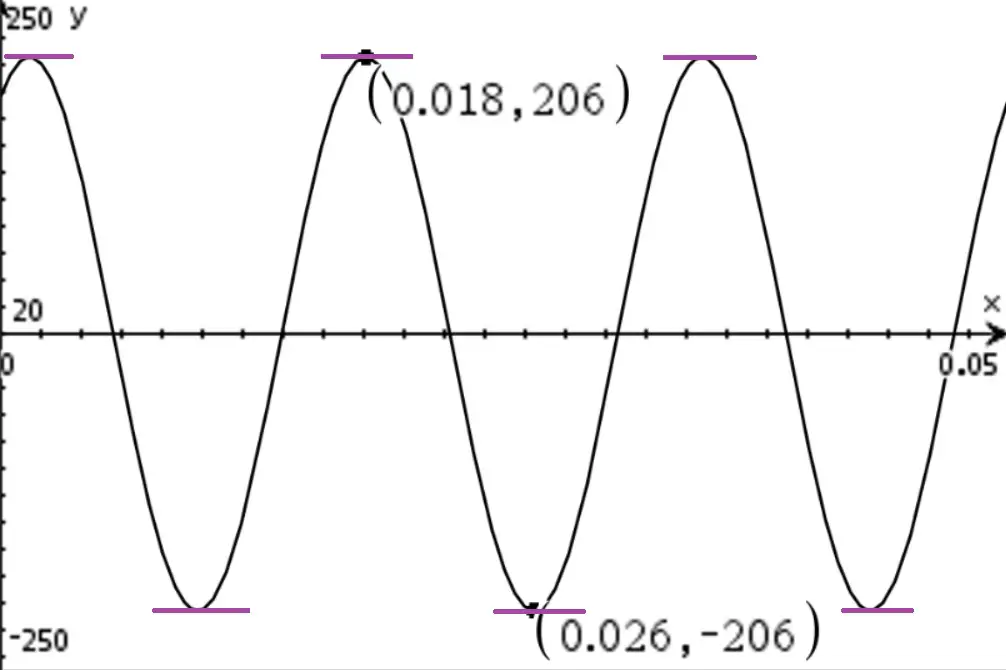 Calculando la derivada de vAB(t) e igualándola a cero podemos obtener cualquiera de esos puntos, ya sea máximos o mínimos, pues en ellos la recta tangente es completamente horizontal. Tiene pendiente cero.
Calculando la derivada de vAB(t) e igualándola a cero podemos obtener cualquiera de esos puntos, ya sea máximos o mínimos, pues en ellos la recta tangente es completamente horizontal. Tiene pendiente cero.
Los cálculos correspondientes a esta parte los presentaré en la calculadora:
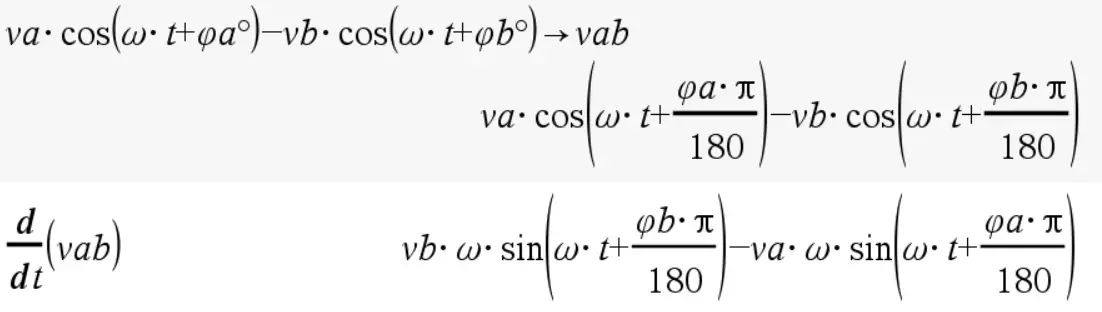 Para facilitar los cálculos en esta etapa le asignaremos una amplitud unitaria a VA y VB, de manera que nuestra expresion final no estará en términos de las amplitudes. Dicho esto, podemos calcular el tiempo en el que la derivada se hace cero:
Para facilitar los cálculos en esta etapa le asignaremos una amplitud unitaria a VA y VB, de manera que nuestra expresion final no estará en términos de las amplitudes. Dicho esto, podemos calcular el tiempo en el que la derivada se hace cero:
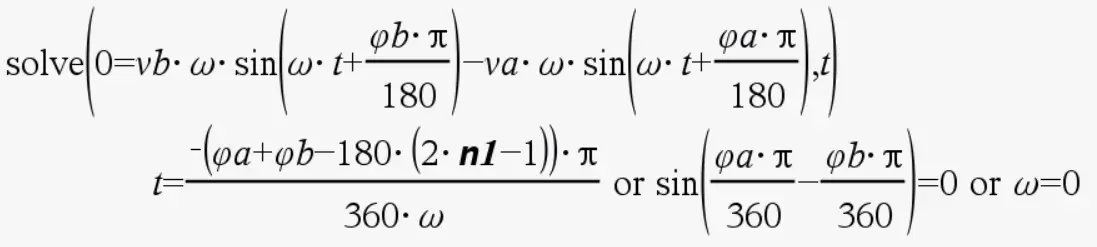 La expresión resultante para el tiempo queda en términos de n1, que es la forma que tiene la calculadora de expresar que se producen múltiples instantes en los que la función vAB(t) alcanza el valor máximo. Esto es propio de cualquier función senoidal o cosenoidal.
La expresión resultante para el tiempo queda en términos de n1, que es la forma que tiene la calculadora de expresar que se producen múltiples instantes en los que la función vAB(t) alcanza el valor máximo. Esto es propio de cualquier función senoidal o cosenoidal.
Para eliminar a n1 asumiremos que solamente se trabajará con máximos locales durante el primer ciclo de la onda senoidal, por lo que n1=1. De esta forma, cuando remplazamos el valor obtenido de t en la función vAB(t) tenemos:
 Si volvemos al paso inmediatamente posterior a la derivada y en vez de asignar valores unitarios a VA y VB veremos que la respuesta sigue siendo la misma, por lo que podemos concluir que esta expresión es independiente de la amplitud de cada fase:
Si volvemos al paso inmediatamente posterior a la derivada y en vez de asignar valores unitarios a VA y VB veremos que la respuesta sigue siendo la misma, por lo que podemos concluir que esta expresión es independiente de la amplitud de cada fase:
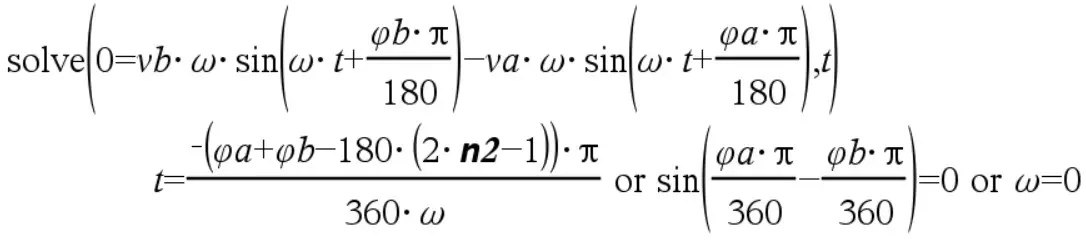 Ahora podemos proceder a probar el modelo matemático con los casos previamente estudiados (amplitudes de 120 y 115 y desfases de 0 y 118):
Ahora podemos proceder a probar el modelo matemático con los casos previamente estudiados (amplitudes de 120 y 115 y desfases de 0 y 118):
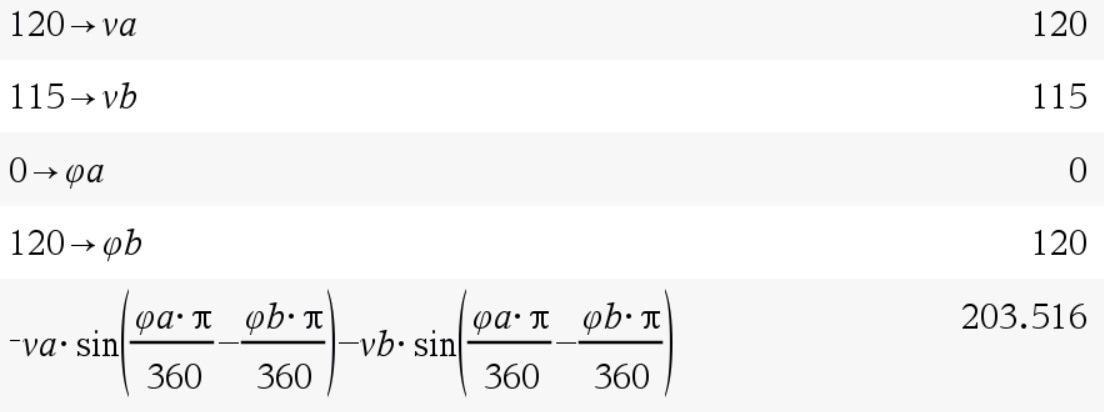
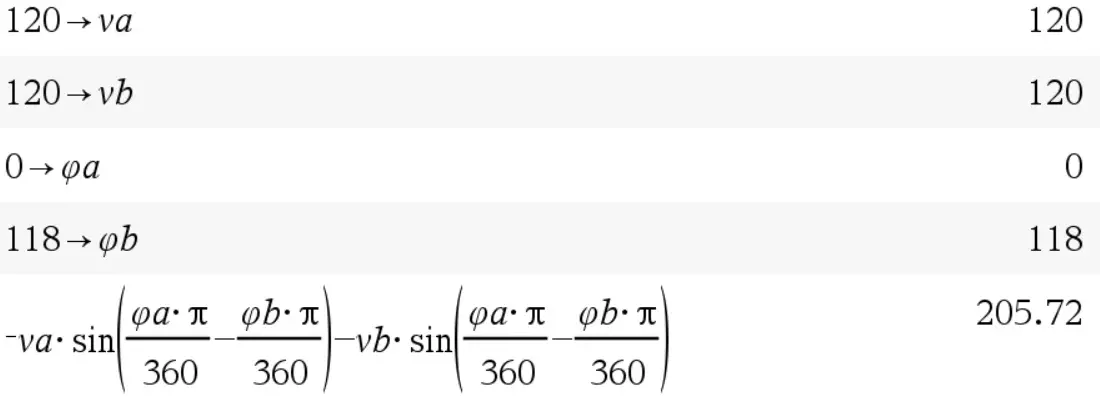 La verdad no se si esto le servirá alguna vez a alguien para algo, pero a mi personalmente me sirvió para entrenar un poco la mente. Siembre es interesante cada vez que tienes que usar los fundamentos de la matemática pra modelar algo, aunque sea muy sencillo.
La verdad no se si esto le servirá alguna vez a alguien para algo, pero a mi personalmente me sirvió para entrenar un poco la mente. Siembre es interesante cada vez que tienes que usar los fundamentos de la matemática pra modelar algo, aunque sea muy sencillo.
Espero que esta información le sea útil a alguien en algún momento. Cualquier duda o comentario es bienvenida en la caja de comentarios.



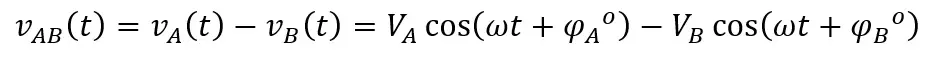









Hola Antony muchísimas gracias por tu aporte, desde hace unos días me viene explotando la cabeza, por este tema, de que ocurre en la realidad y como calcular los valores reales en voltajes de linea si las bobinas de mi generador no están perfectamente desfasadas 120 grados una de otra, a partir de tu aporte pude realizar mis propios cálculos
Qué bueno que te sirvió este contenido. Graciad por comentar.