La ley de Ohm no es solo una de las leyes fundamentales de la electricidad, sino también un pilar esencial del conocimiento para aquellos que se adentran en el mundo de los circuitos eléctricos y electrónicos. Esta ley, propuesta por el físico alemán Georg Simon Ohm en 1827, establece una relación directa entre el voltaje, la corriente y la resistencia en un circuito eléctrico. En términos sencillos, nos dice cuánta corriente fluirá a través de un componente, como una resistencia, cuando se le aplica una diferencia de potencial o voltaje.
Más que una herramienta tangible, es un principio que guía y facilita nuestra comprensión del comportamiento eléctrico. Nos permite predecir y calcular cómo actuarán los componentes en un circuito, y cómo las variaciones en uno de los parámetros (como la resistencia) pueden afectar a los demás (como el voltaje o la corriente). Esto es especialmente útil para diseñar y diagnosticar circuitos, garantizando su correcto funcionamiento y evitando posibles fallos o problemas.
Para quienes trabajan o estudian en el ámbito eléctrico, comprender y aplicar la ley de Ohm es crucial. No solo es la base para el diseño y análisis de circuitos, sino que también sirve como una introducción al estudio más profundo de la teoría eléctrica y electrónica. En la práctica diaria, ya sea en la investigación, la industria o la educación, esta ley se convierte en una herramienta indispensable que todo profesional o estudiante debe dominar a la perfección.
¿Qué expresa la ley de Ohm?
Pues la Ley de Ohm establece las relaciones que existen entre potencial eléctrico (voltaje), corriente eléctrica y la resistencia. La Ley de Ohm expresa que: la corriente eléctrica a través de un conductor será igual a la diferencia de potencial entre la resistencia que halla en dicho conductor, es decir:
donde I es la intensidad o corriente eléctrica medida en Amperios. V es el potencial o voltaje medido en voltios. R es la resistencia medida en Ohms.
¿Qué significa esto?
Para poder que se produzca una corriente eléctrica a través de un conductor es necesario que exista una diferencia de potencial entre 2 puntos y ocurra un flujo de cargas eléctricas. Esto ya lo vimos en nuestro anterior post.
[youtube https://www.youtube.com/watch?v=Mk_l5OCFLK8]
En todo conductor siempre vamos a encontrar una resistencia eléctrica, aunque sea muy pequeña. Los mejores conductores que existen poseen resistencia de unos cuantos Ohm y la misma varía en función de la longitud del conductor. En fin, la corriente depende del voltaje y de la resistencia que halla en determinado conductor. Eso es todo.
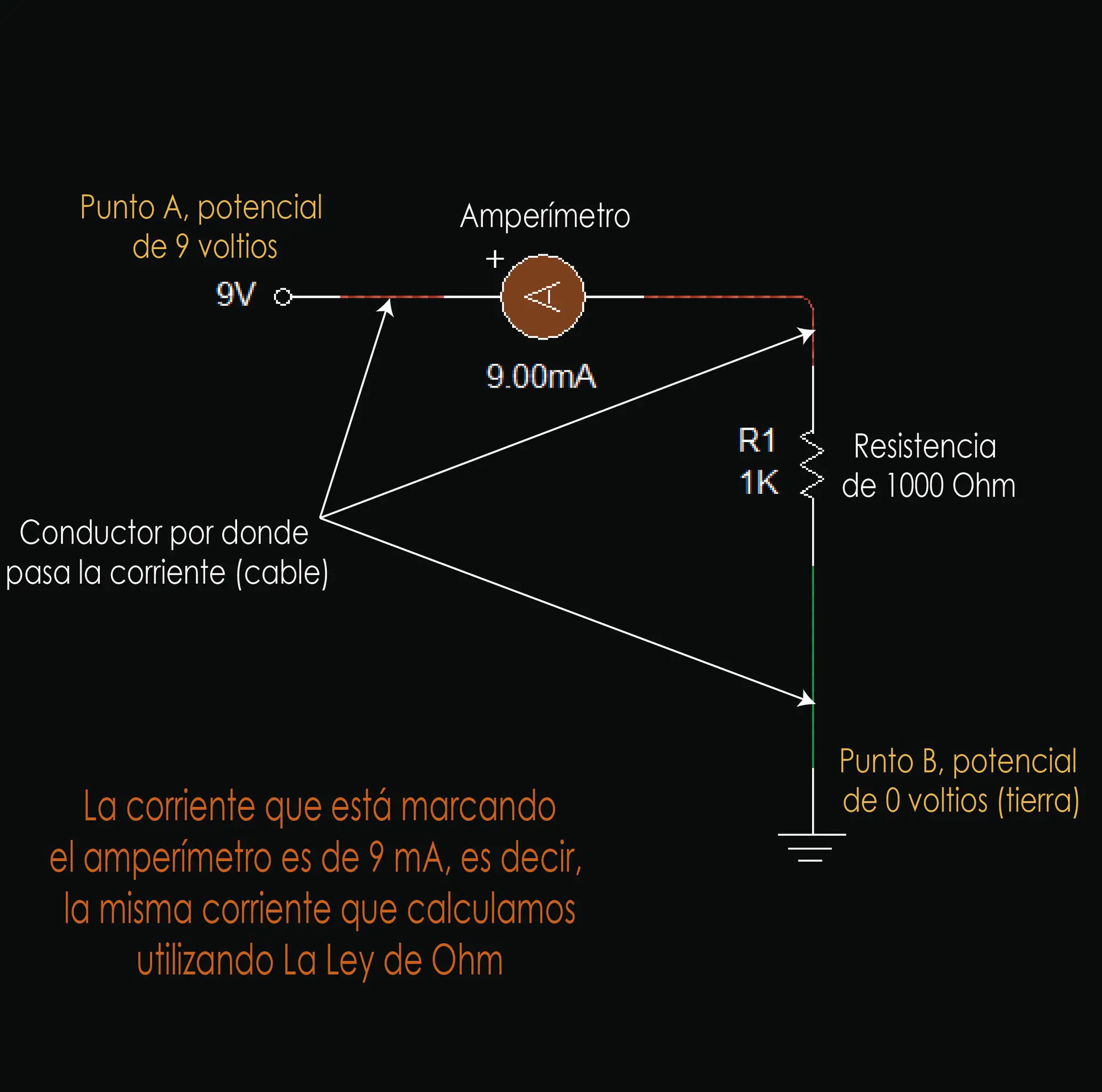
Veamos un sencillo ejemplo. Usaremos un amperímetro que es un dispositivo capaz de medir la cantidad de corriente que fluye a través de un conductor. Si tenemos un conductor y en uno de los extremos de ese conductor existe un potencial eléctrico de 9 voltios, el otro extremo se conecta a tierra, es decir, a un potencial de 0 voltios, habrá una diferencia de potencial de 9 voltios. Si en ese conductor hay presente una resistencia de 1 KOhm (1000 Ohms), la corriente eléctrica en ese conductor será igual a:
La corriente eléctrica que pasa a través de dicho conductor será de 9 mili amperios. Veamos una representación gráfica de esto:
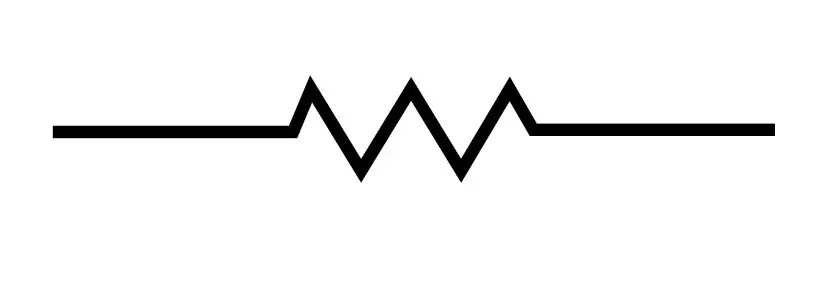
Como vemos, en este esquema hay un cable con una diferencia de potencial y una resistencia. El símbolo de la resistencia es parecido a un zig zag:
Cada vez que veamos este símbolo sabemos que hay una resistencia en el conductor que estemos estudiando. Estas resistencias pueden ser de valores tan pequeños como 0.1 Ohm hasta valores en el orden de los Mega Ohm (un millón de Ohms).
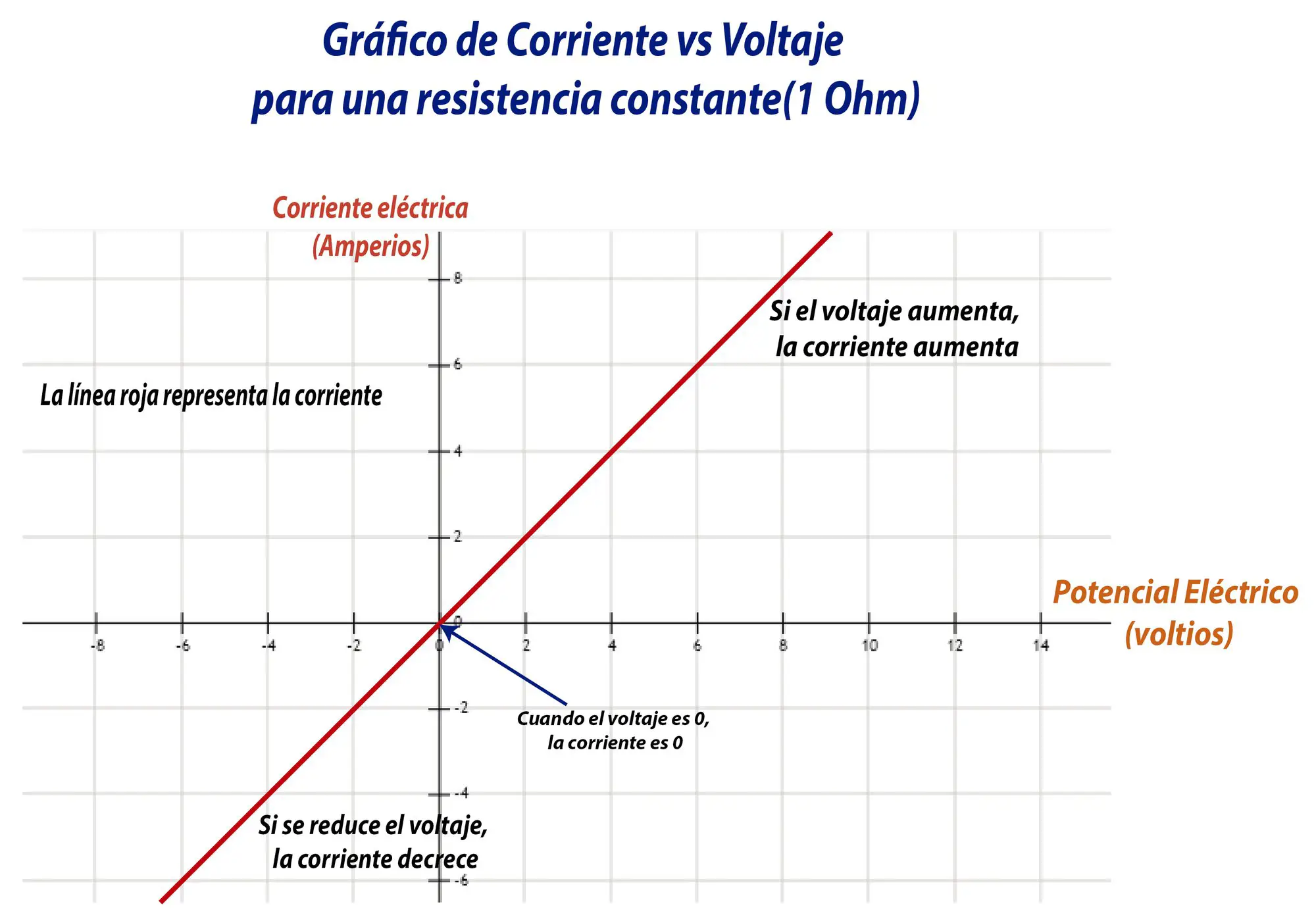
Entre más grande sea la resistencia, menor es la corriente que fluye a través de un conductor, es decir, hay más oposición al paso de las cargas. Entre mayor sea la diferencia de potencial entre los extremos de un conductor, mayor será la corriente que fluya a través de el. Dicho esto podemos deducir que la corriente es directamente proporcional al voltaje e inversamente proporcional a la resistencia. La mejor manera de comprender estos fenómenos es a través del análisis gráfico.
En este gráfico la línea roja es la corriente. A medida que el voltaje en el eje horizontal decrece, el valor de la corriente se reduce. Tanto la corriente como el voltaje pueden adoptar valores negativos, a diferencia de la resistencia que solamente puede tener valores positivos.
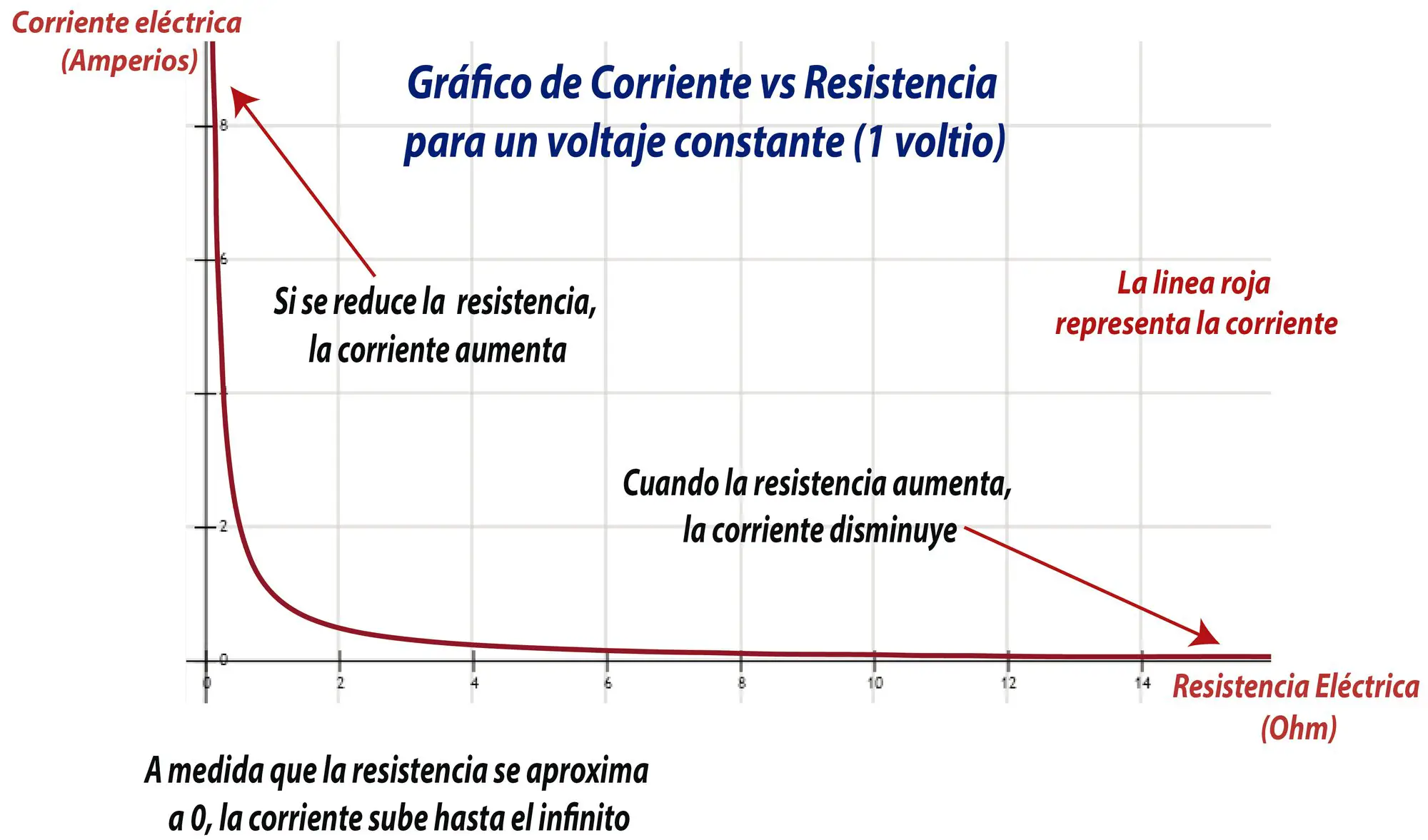
En este gráfico la curva roja representa la corriente. En el eje horizontal está la resistencia. Si la resistencia es cercana a 0, la corriente es muy alta. A medida que el valor de la resistencia va aumentando en el eje horizontal, la corriente se va haciendo más pequeña.
Algo muy importante que debemos saber todos es lo que sucede con la corriente cuando la resistencia es 0 o cercana a 0.
Si tenemos por ejemplo un conductor en el cual uno de los extremos está a un potencial de 10 voltios y en el otro extremo lo colocamos a un potencial de 0 voltios, habrá una diferencia de potencial. Si el conductor es un cable de cobre, la resistencia será muy pequeña, casi 0. Si dividimos el voltaje entre la resistencia el resultado será el siguiente:
Según el cálculo, cualquier número dividido entre 0 tiende al infinito. Una corriente infinita. No existe todavía ningún dispositivo capaz de soportar una corriente infinita. Los conductores o cables solamente soportan determinada cantidad de corriente. Si el flujo de cargas es demasiado alto para un conductor muy pequeño, el mismo no podrá soportar tanta energía, se calentará y se fundirá. Esto podría causar chispas y explosiones. Al fenómeno de la corriente infinita a través de un conductor se le conoce como corto circuito.
Es el corto circuito lo mismo que sucede en nuestros hogares cuando 2 cables se chocan. Son 2 conductores a potenciales distintos con una resistencia cercana a 0. Una corriente demasiado alta para la soportada por el conductor se produce y causa chispas, explosiones, los cables se derriten y eventualmente es lo que causa incendios. Es extremadamente peligroso.
Algo similar sucede con nosotros los seres humanos. El cuerpo humano posee una resistencia al paso de la electricidad. La misma varía dependiendo de una serie de factores (estado físico, masa corporal, estatura, incluso el humor). La resistencia aproximada del cuerpo humano varía entre 500 y 3000 Ohm (2.5 KOhm).
Si nuestro cuerpo se somete a un potencial alto, como el del suministro eléctrico (120 voltios AC), tomando en cuenta que nuestro cuerpo esta sobre el piso, es decir, tierra a un potencial de 0 voltios, se producirá una diferencia de potencial (120 voltios) entre los extremos de un conductor (el cuerpo humano). Calculemos la corriente que pasará a través de nuestro cuerpo (para una resistencia de 2000 Ohm):
El paso de una corriente así por nuestro cuerpo causará estragos. El corazón de una persona podría detenerse con una descarga de 30mA, es decir, estaríamos recibiendo el doble de la corriente que podría detener nuestro corazón. Esto podría detener la respiración, contraer músculos (las neuronas funcionan con pulsos eléctricos), al sangre se disocia los órganos se destruyen y podría causar la muerte. La corriente es muy interesante pero peligrosa a la vez.
En fin, para llegar a todas estas conclusiones hemos utilizado un principio muy sencillo, la Ley de Ohm.
Resistencias en Serie y Paralelo
La resistencia eléctrica en un conductor se puede manipular agregando resistores:
Los resistores poseen distintos valores de resistencia y son utilizadas en la confección de circuitos según las necesidades del diseñador para limitar la corriente y causar caídas de voltaje, entre muchas otras aplicaciones. Aumentar o reducir el valor de la resistencia en un circuito modifica la corriente que fluye a través de él.
Ahora trataré algunas propiedades de los resistores.
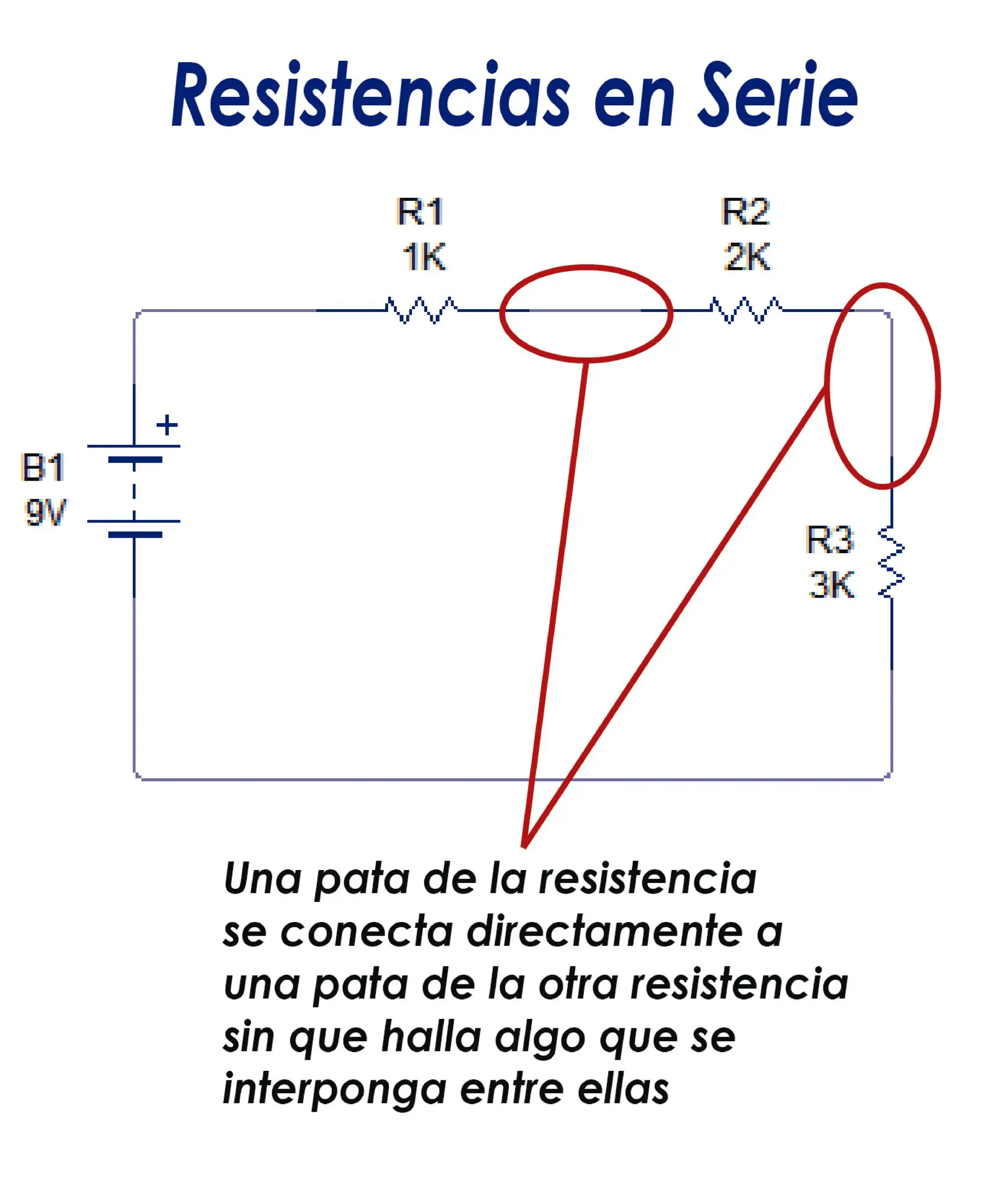
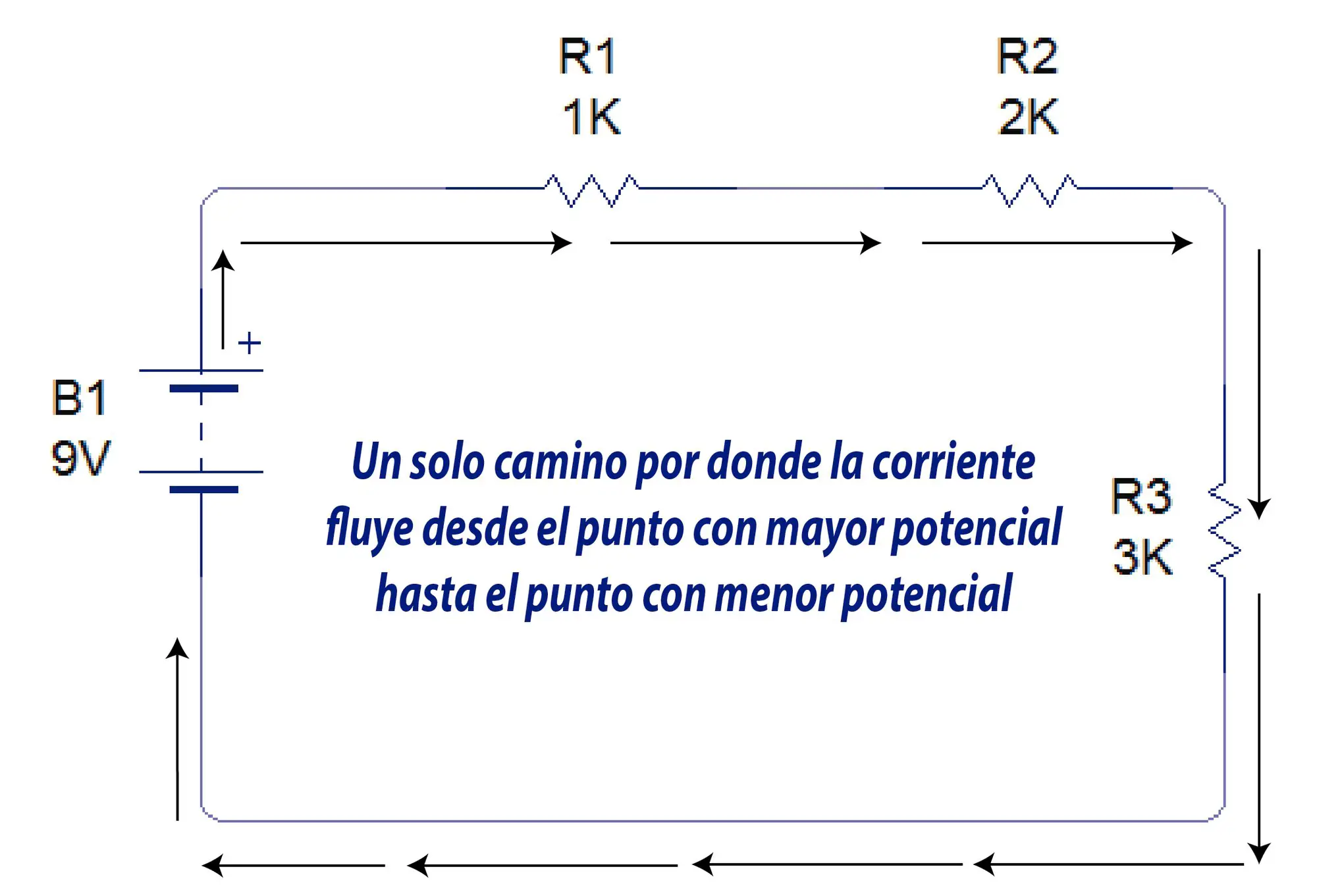
- Conexión en Serie
Un terminal o pata de una resistencia va conectado directamente a la otra pata o terminal de otra resistencia, sin que halla alguna otra conexión que se interponga entre ellas.
Este tipo de conexión se caracteriza porque la corriente tiene un solo camino para llegar desde el punto con mayor potencial hasta el punto con menor potencial.
Solo hay una sola manera en la que la corriente puede fluir hasta el punto con menor potencial.
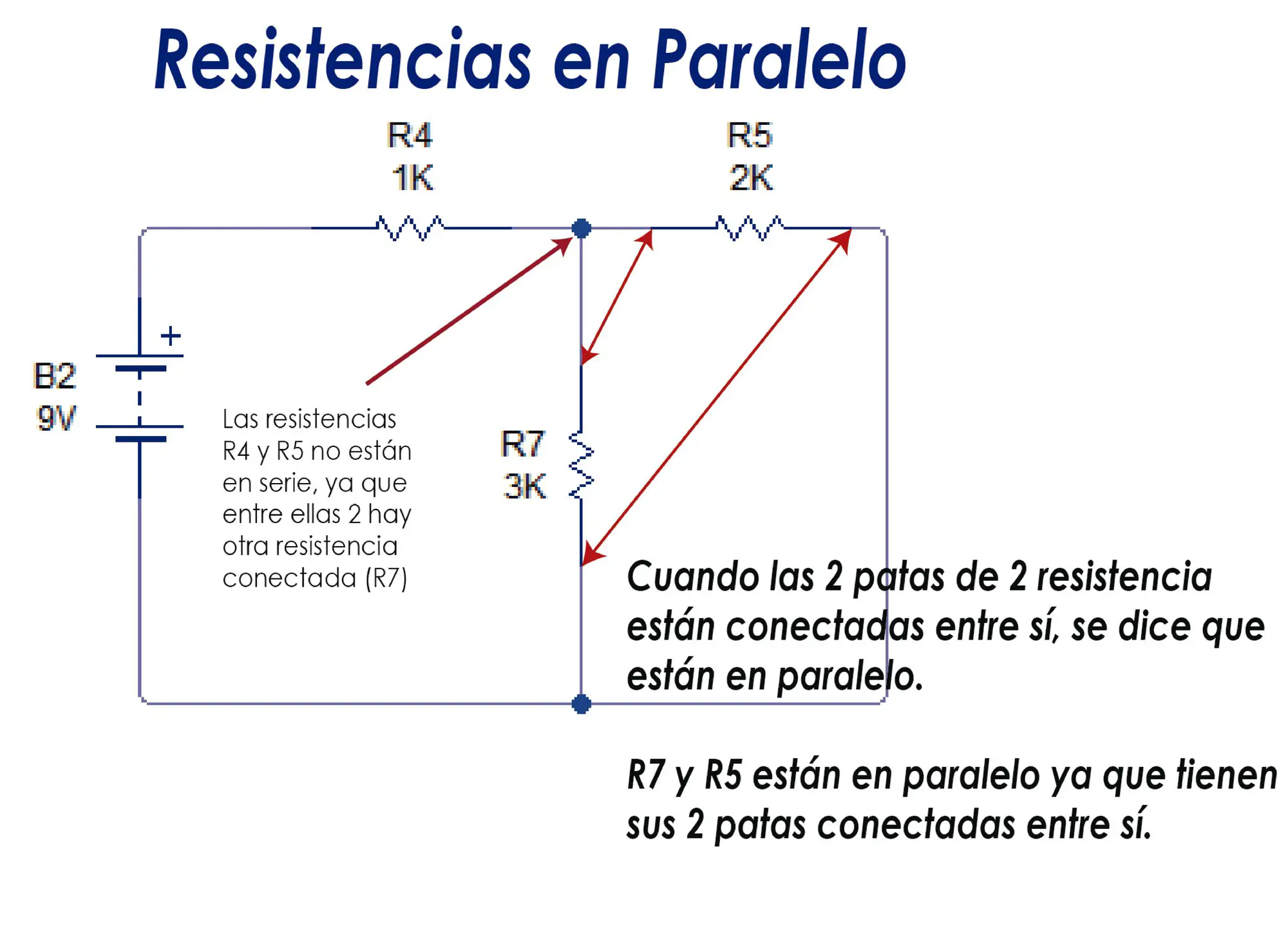
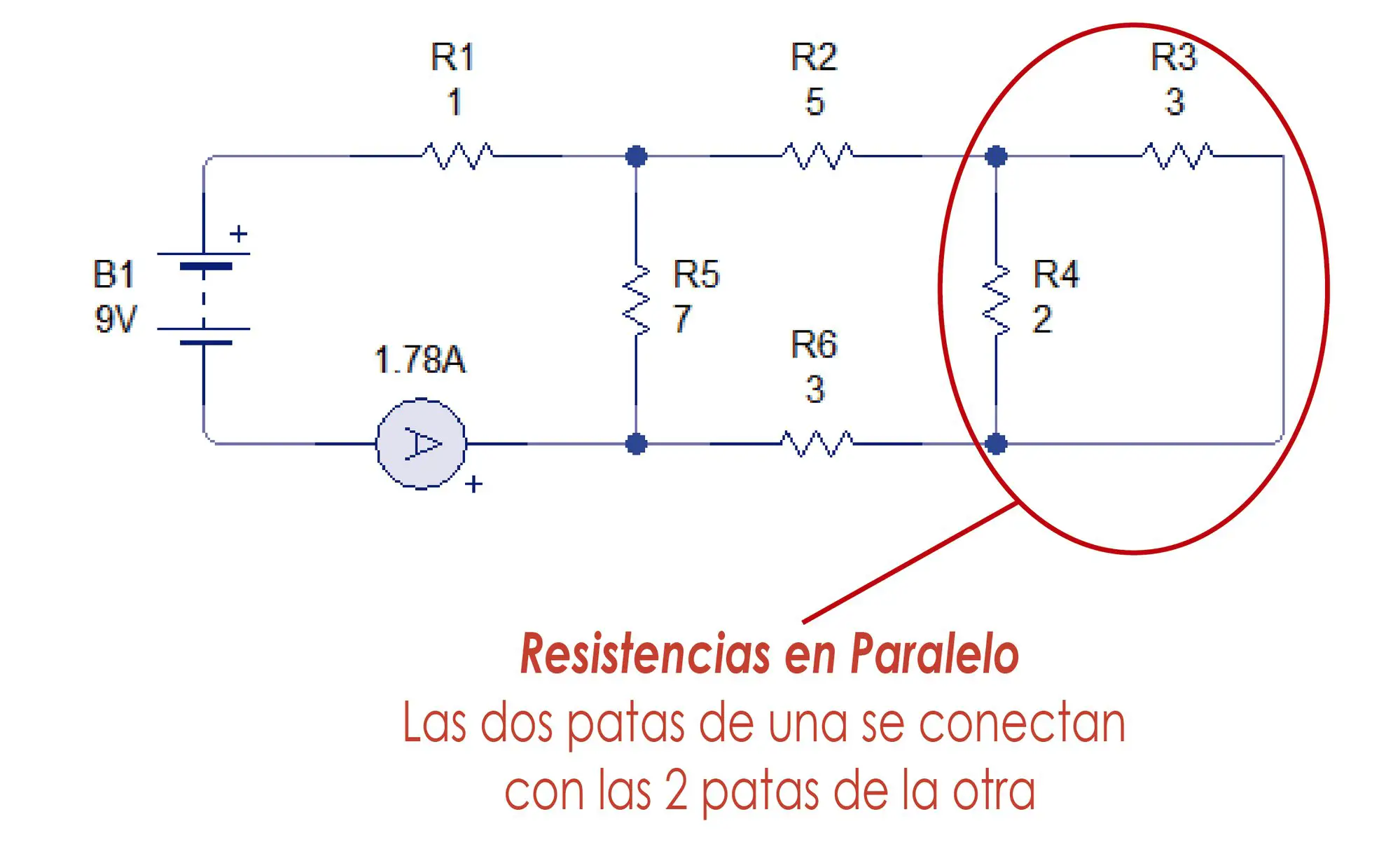
- Resistencias en Paralelo
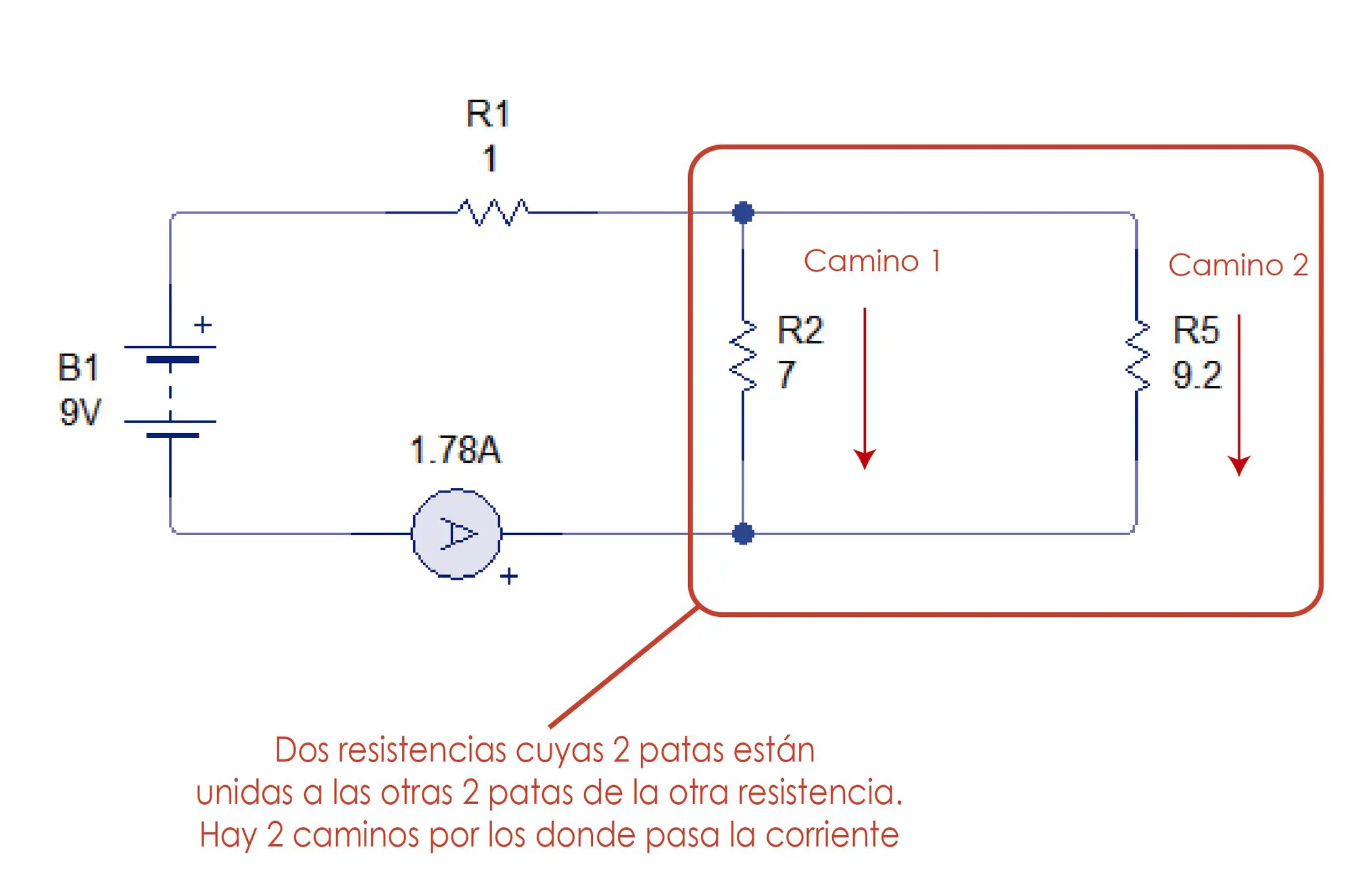
Las resistencias en paralelo están inter conectadas entre sí de tal manera que las 2 patas de una resistencia están conectadas a las 2 patas de otra resistencia.
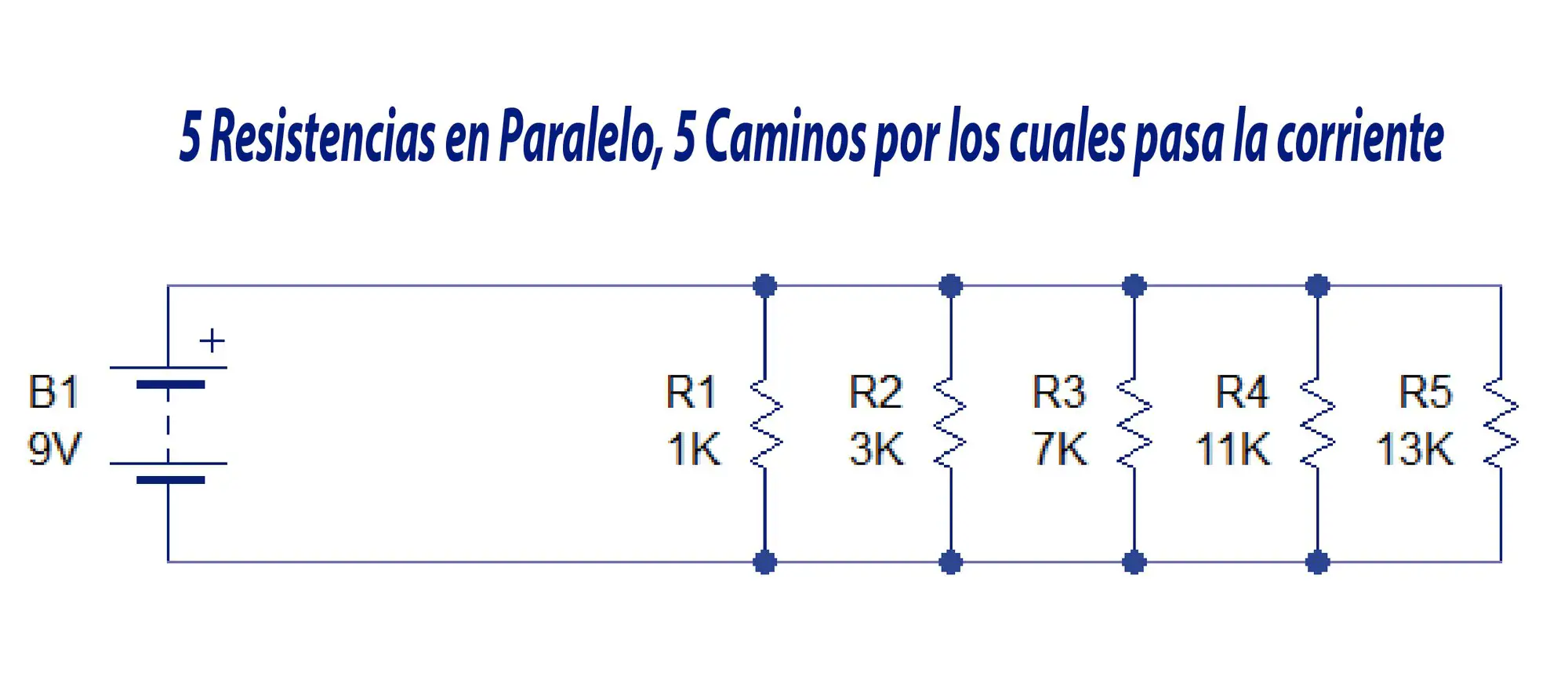
En la conexión en paralelo hay más de 1 camino por el cual la corriente puede llegar a tierra.
La corriente pasará por cada uno de los 5 caminos proporcionalmente a la cantidad de resistencia que halla en cada camino.
Resistencia Equivalente
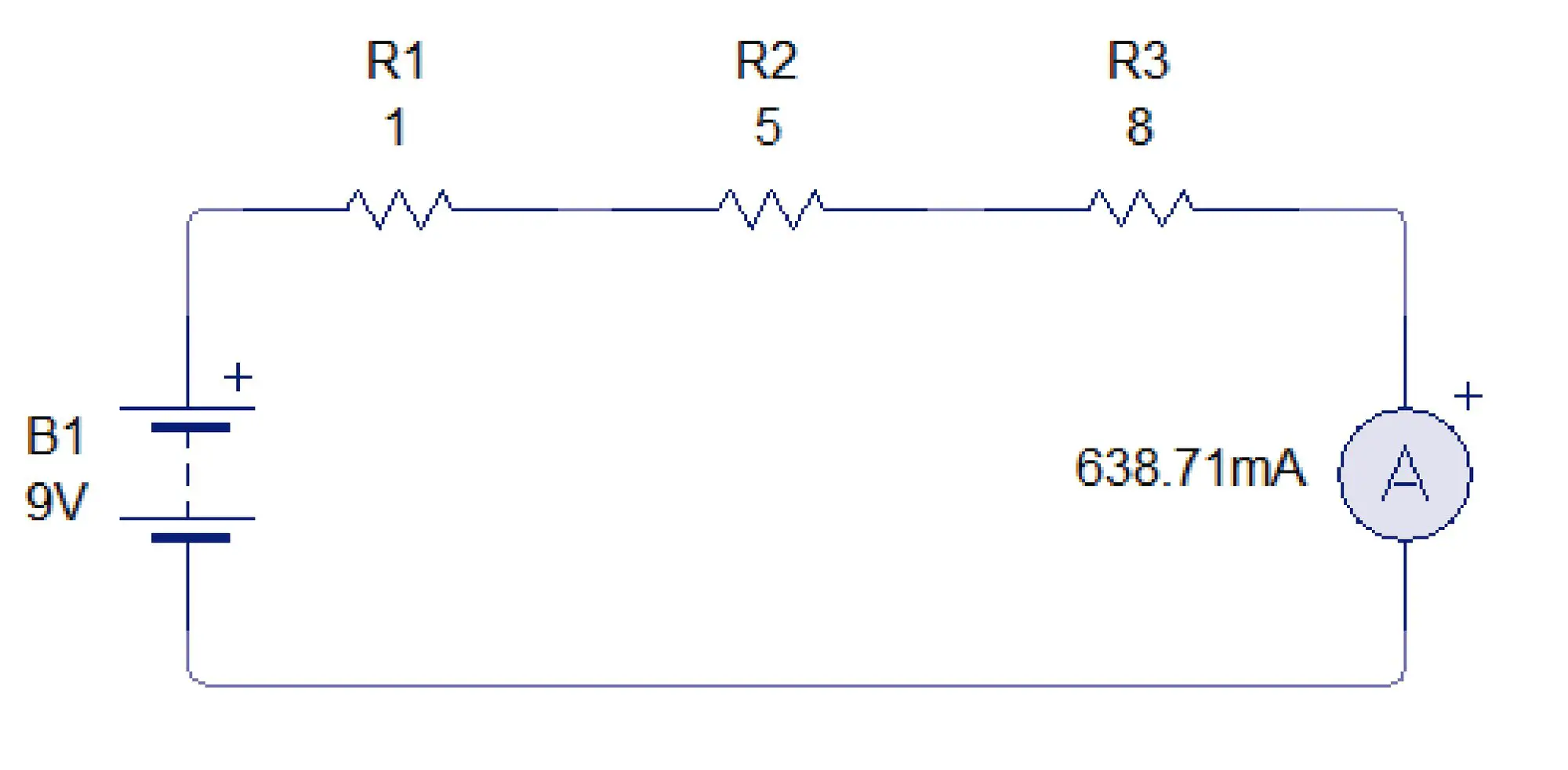
La resistencia equivalente es aquella resistencia por la cual podríamos reemplazar un grupo de resistencias sin afectar la corriente en el circuito. Si las resistencias están en serie, basta con sumarlas algebraicamente para encontrar la resistencia equivalente.
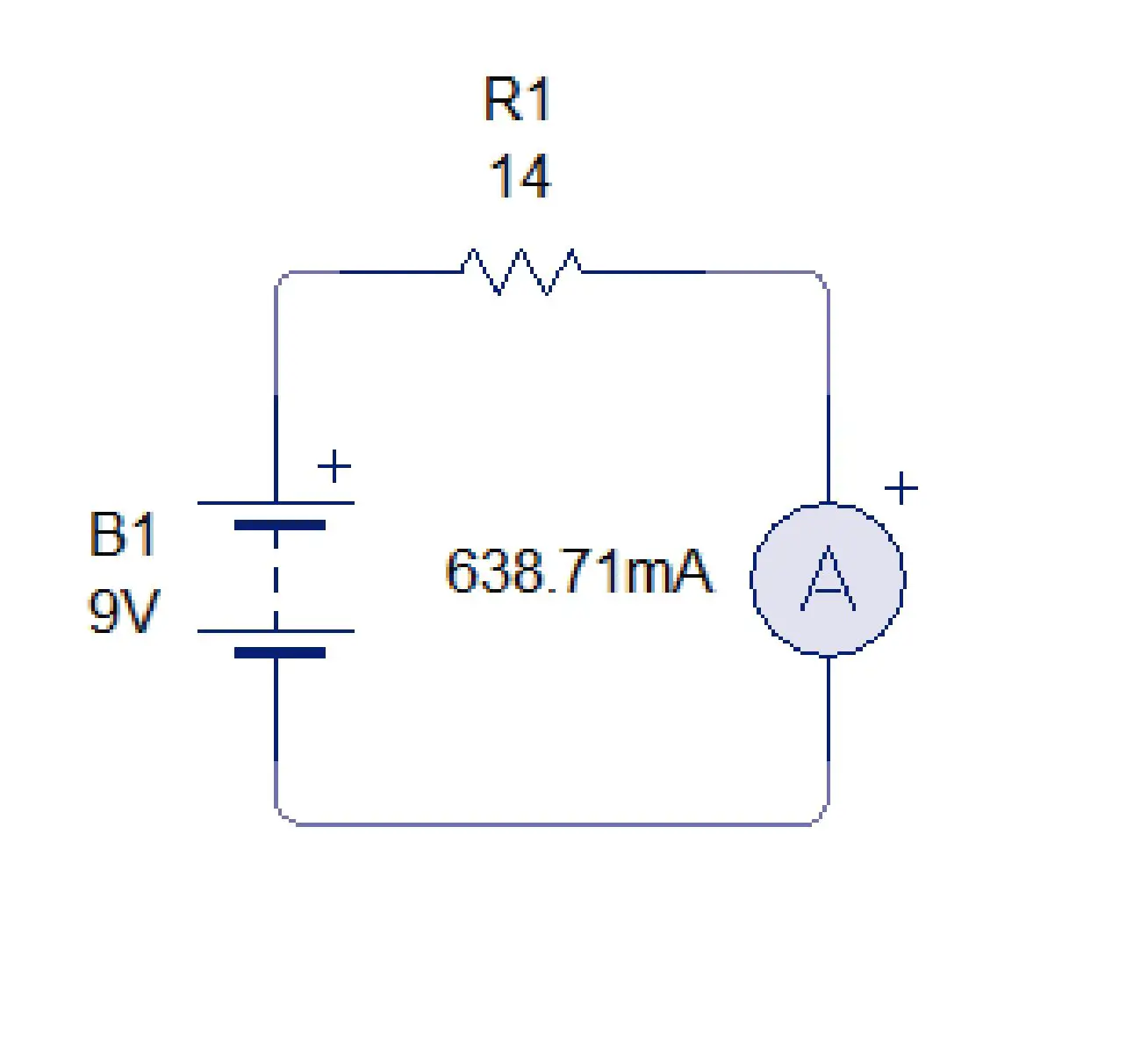
En este circuito con 3 resistencias, la corriente que medimos con el amperímetro es de 638.71 mA. Si sumamos algebraicamente estas 3 resistencias que estan en serie tenemos que:
Req=1+5+8=14 Ω
Si remplazamos esas 3 resistencias por una sola resistencia de 14 Ω obtenemos la misma corriente:
En la imagen se puede observar que al remplazar la resistencia equivalente, la corriente no cambia. En los circuitos con resistencias en paralelo el proceso es diferente.
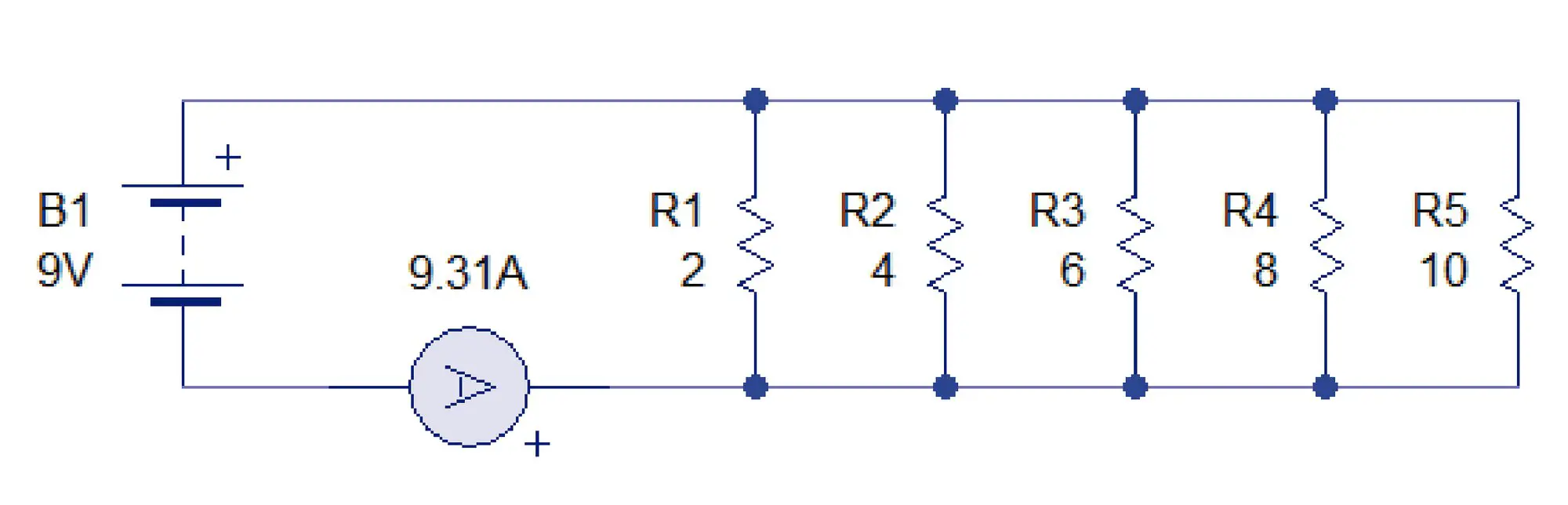
Lo primero que podemos observar es que la corriente es extremadamente alta (9.31 Amperios). Esto se debe a que la corriente tiene 5 caminos para llegar desde el punto con mayor potencial hasta el punto con menor potencial. Entre más caminos halla, más corriente podrá fluir.
La resistencia debe ser pequeña entones (menor a 1). Para buscar la resistencia equivalente de resistores en paralelo se deben sumar las conductancias, es decir, el inverso de la resistencia.
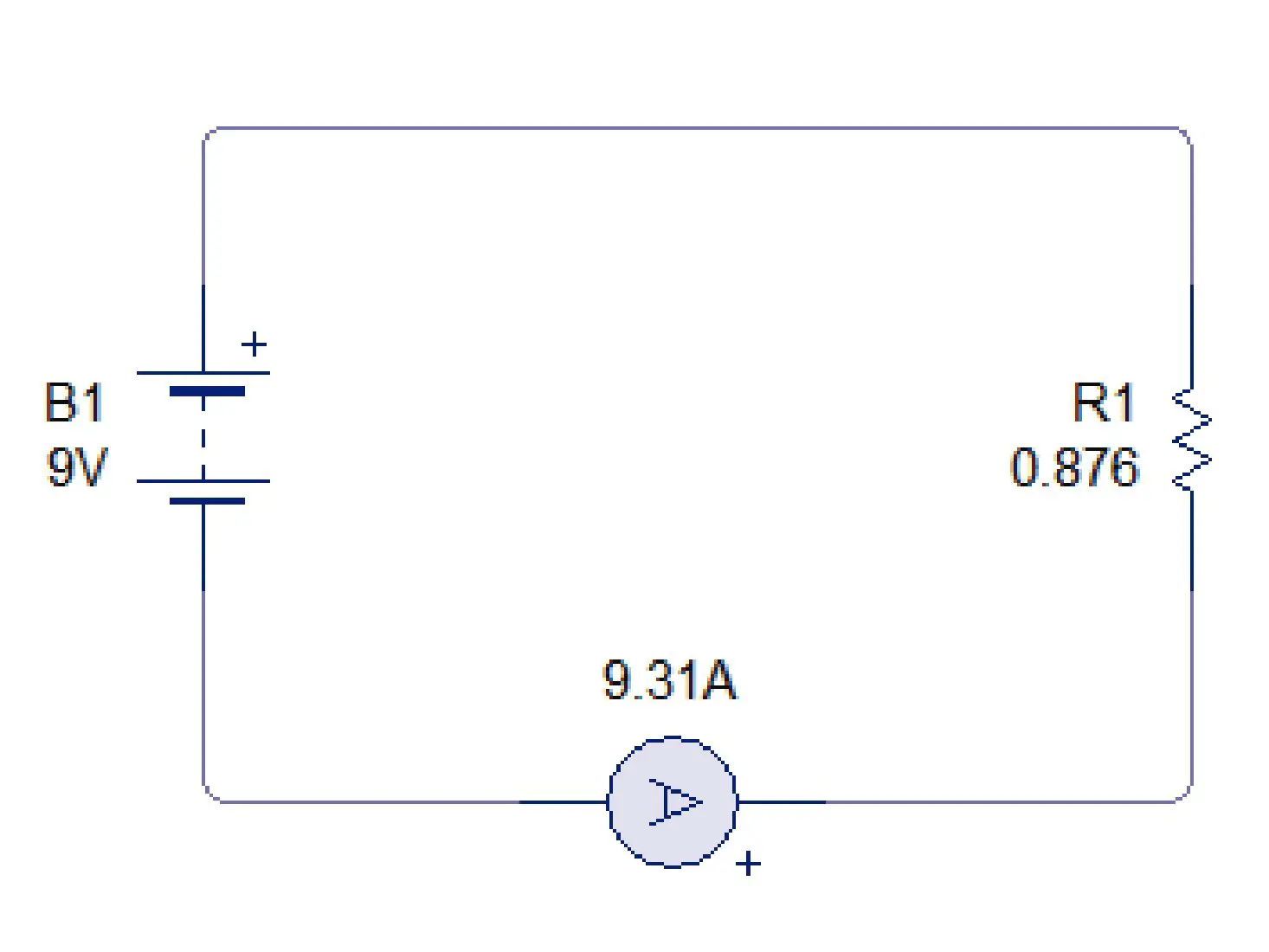
La resistencia equivalente en paralelo es el inverso de la conductancia (G). Por eso se coloca 1/R. Cuando se suman las conductancias, se invierte el numerador con el denominador y se obtiene la resistencia equivalente. Ahora vamos a remplazar esa resistencia equivalente en el circuito y ver que sucede.
Como vemos al remplazar las 5 resistencias por su resistencia equivalente se obtiene la misma corriente en el circuito.
Combinaciones de resistencias en serie y paralelo
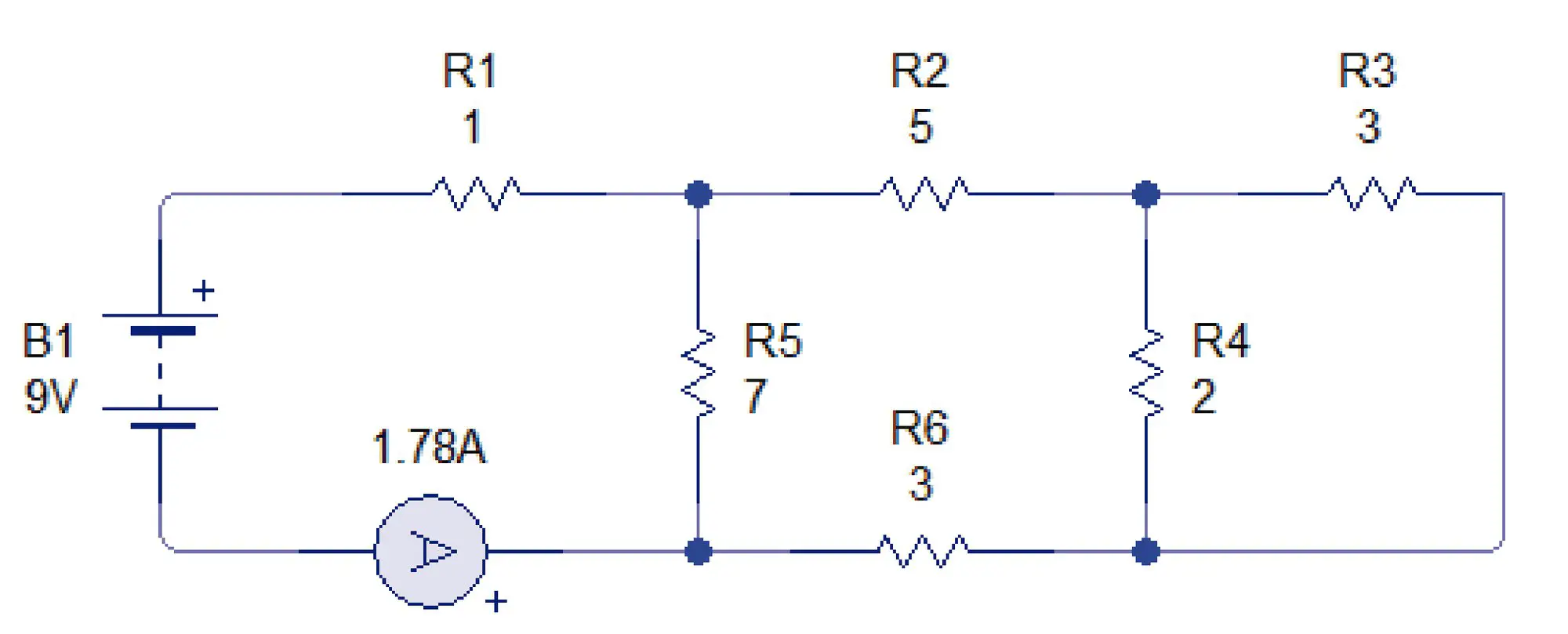
Cuando hay resistencias combinadas en serie y paralelo podemos encontrar una sola resistencia equivalente que remplace todas las resistencias.
Para hallar la resistencia equivalente de este circuito, generalmente se busca un extremo del diagrama en donde se pueda identificar si una resistencia está en serie o paralelo.
Al identificar 2 resistencias en paralelo, se busca su resistencia equivalente y se remplaza las 2 resistencias en paralelo por una sola resistencia.
Se reemplaza por la resistencia equivalente.
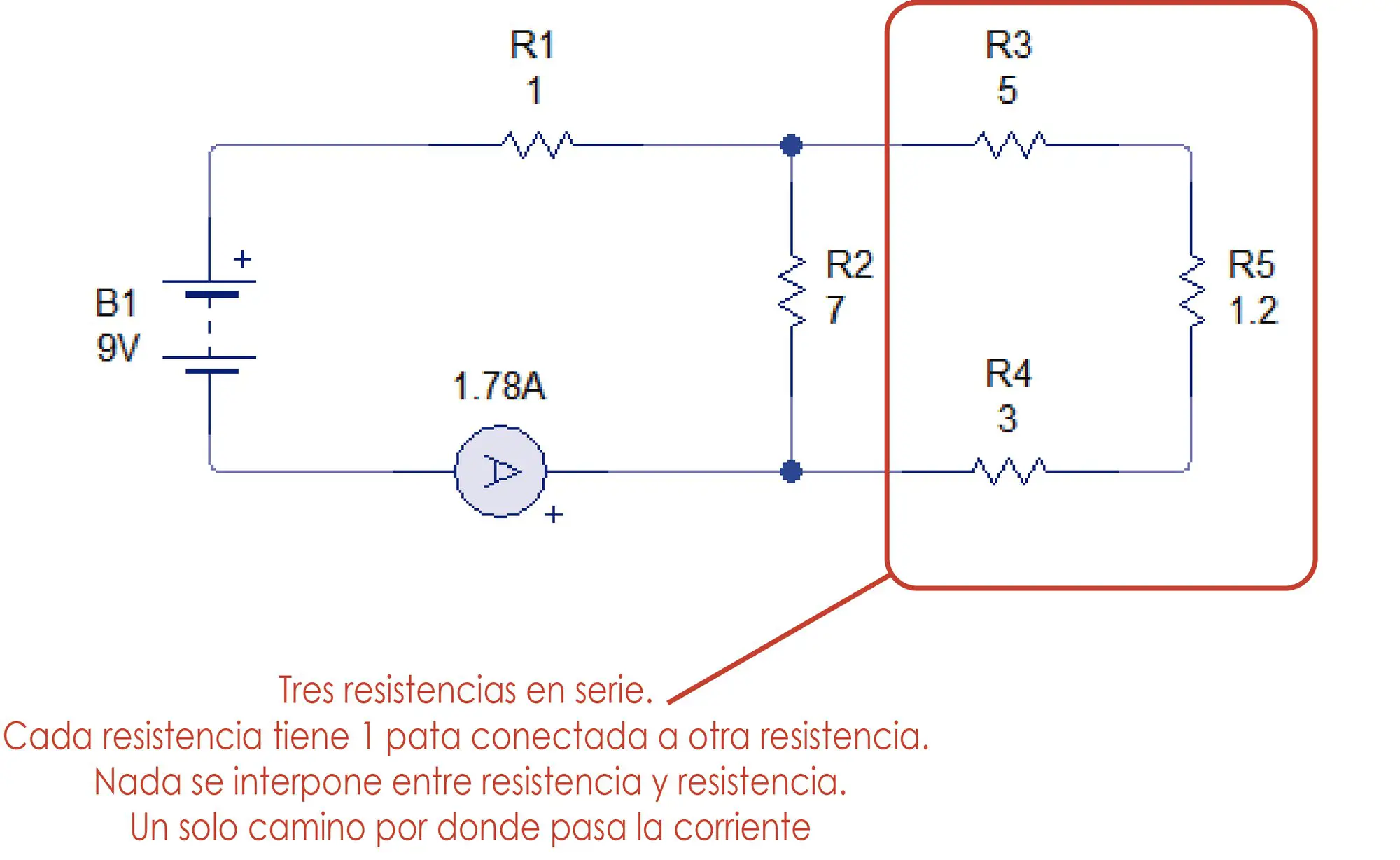
Ahora seguimos identificando las resistencias que se pueden reducir.
Como las 3 resistencias R3, R4 y R5 están en serie, las sumamos algebraicamente.
Req = 5+3+1.2=9.2 Ω
Reemplazamos las 2 resistencias por una sola.
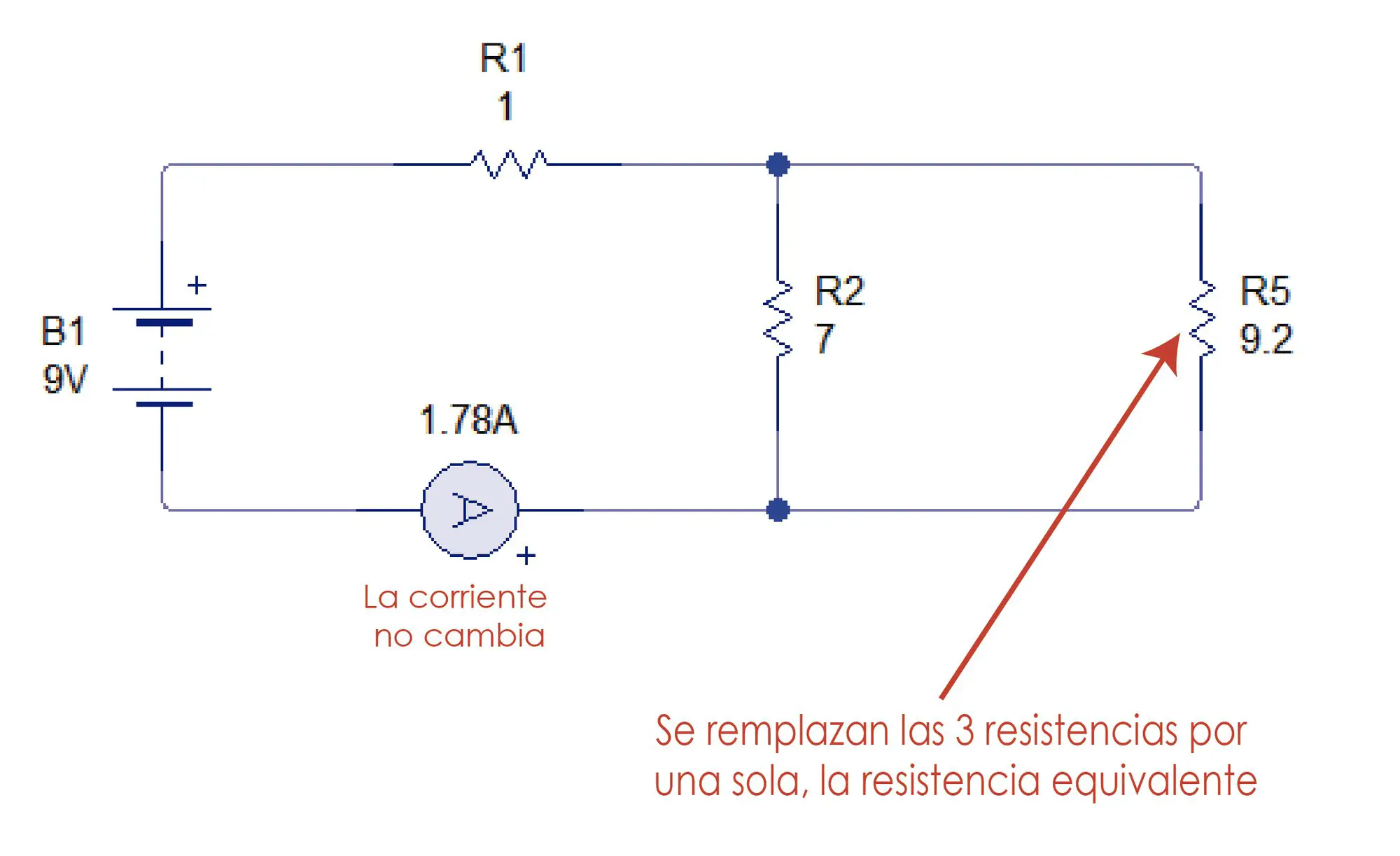
Ahora en el extremo derecho podemos identificar 2 resistencias en paralelo.
Ahora buscamos la resistencia equivalente de R2 y R5.
Se remplaza las 2 resistencias por una sola.
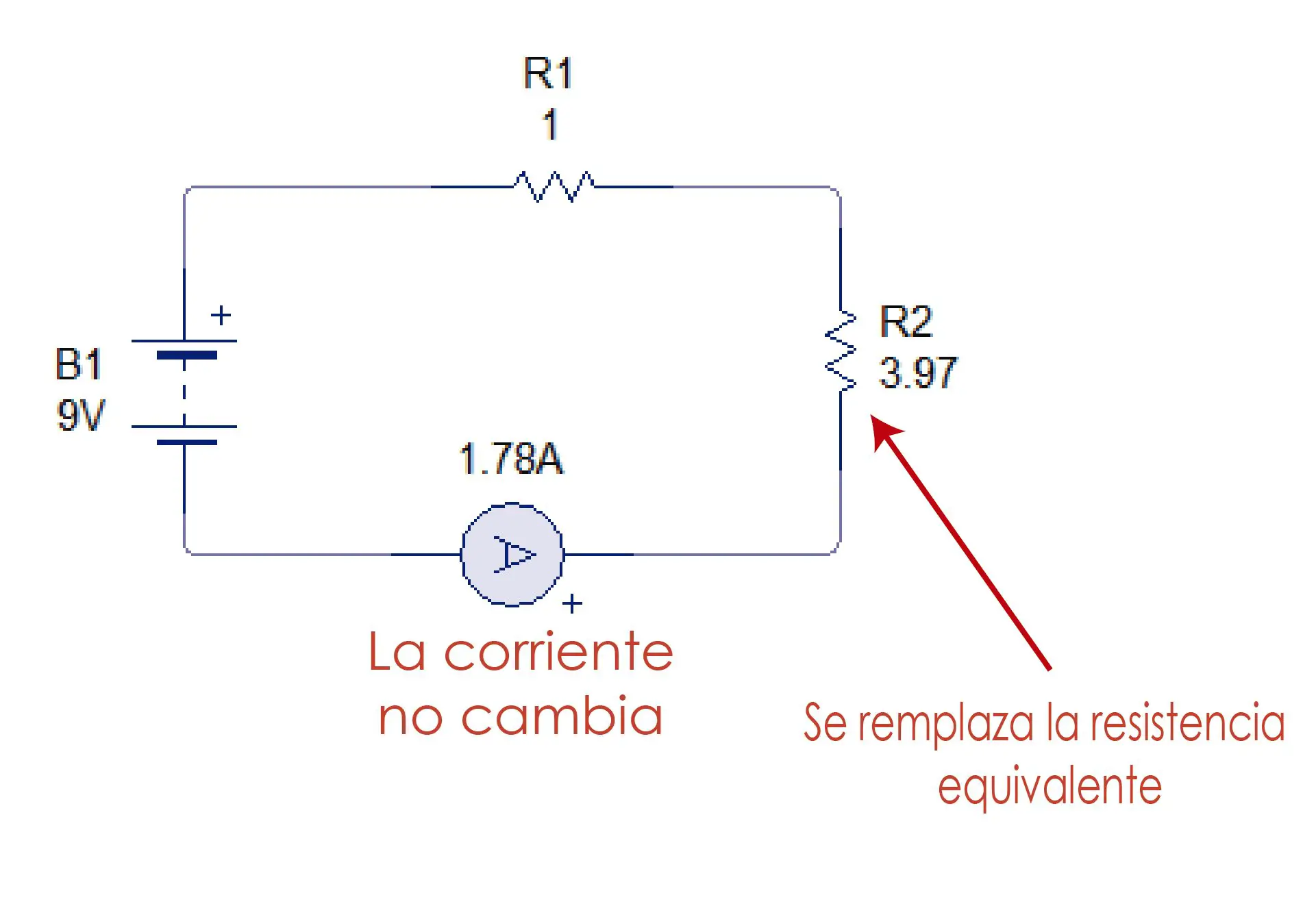
Por último nos quedan 2 resistencias en serie. Buscamos la equivalente y reemplazamos.
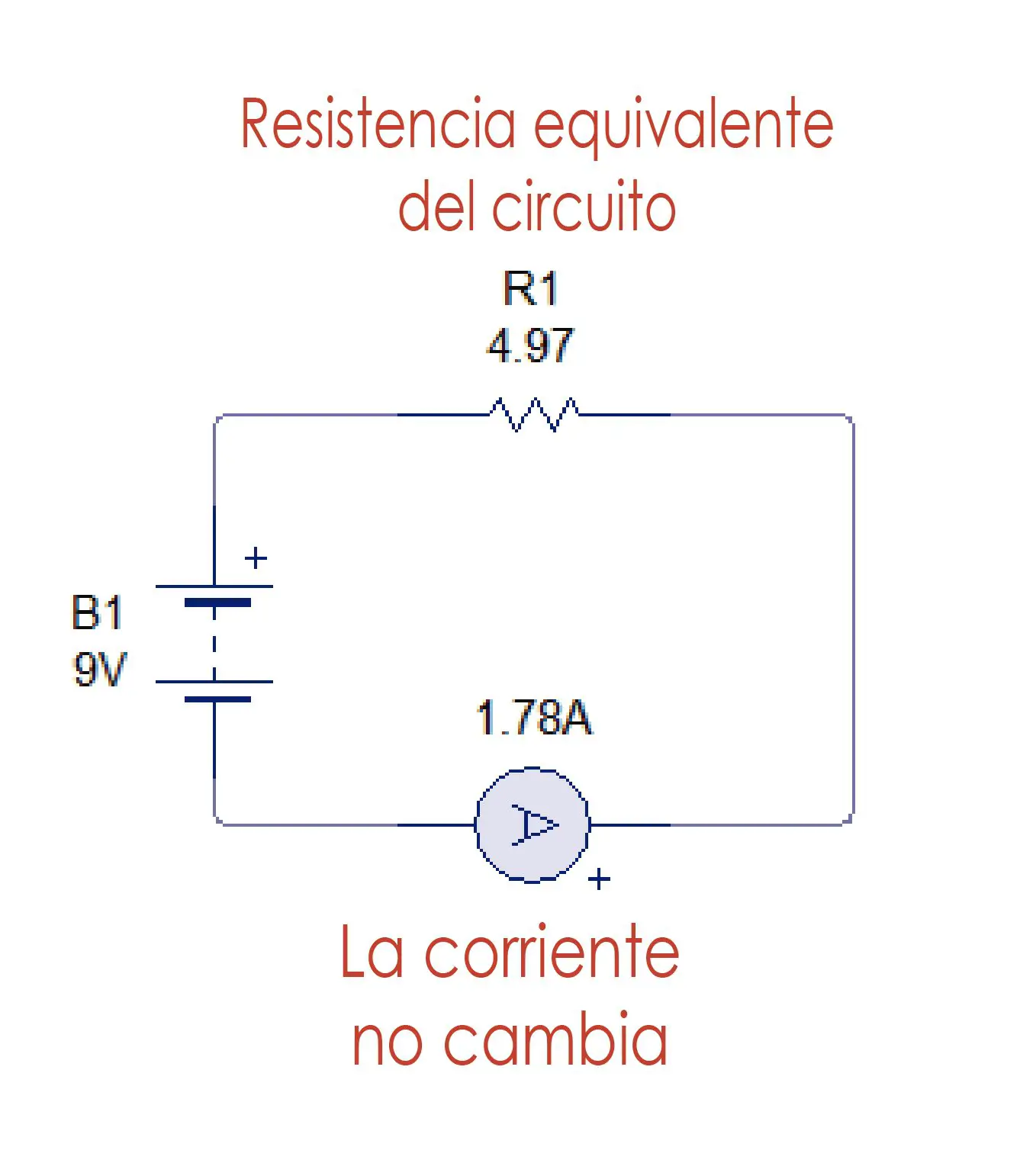
Req= 1+ 3.97 = 4.97 Ω
Como podemos observar, la corriente no varía. Las resistencias de la primera figura han sido reducidas a una sola que representa todas las demás resistencias.
Caídas de voltaje y división de corriente
Cuando se trabaja con resistencias hay 2 simples principios:
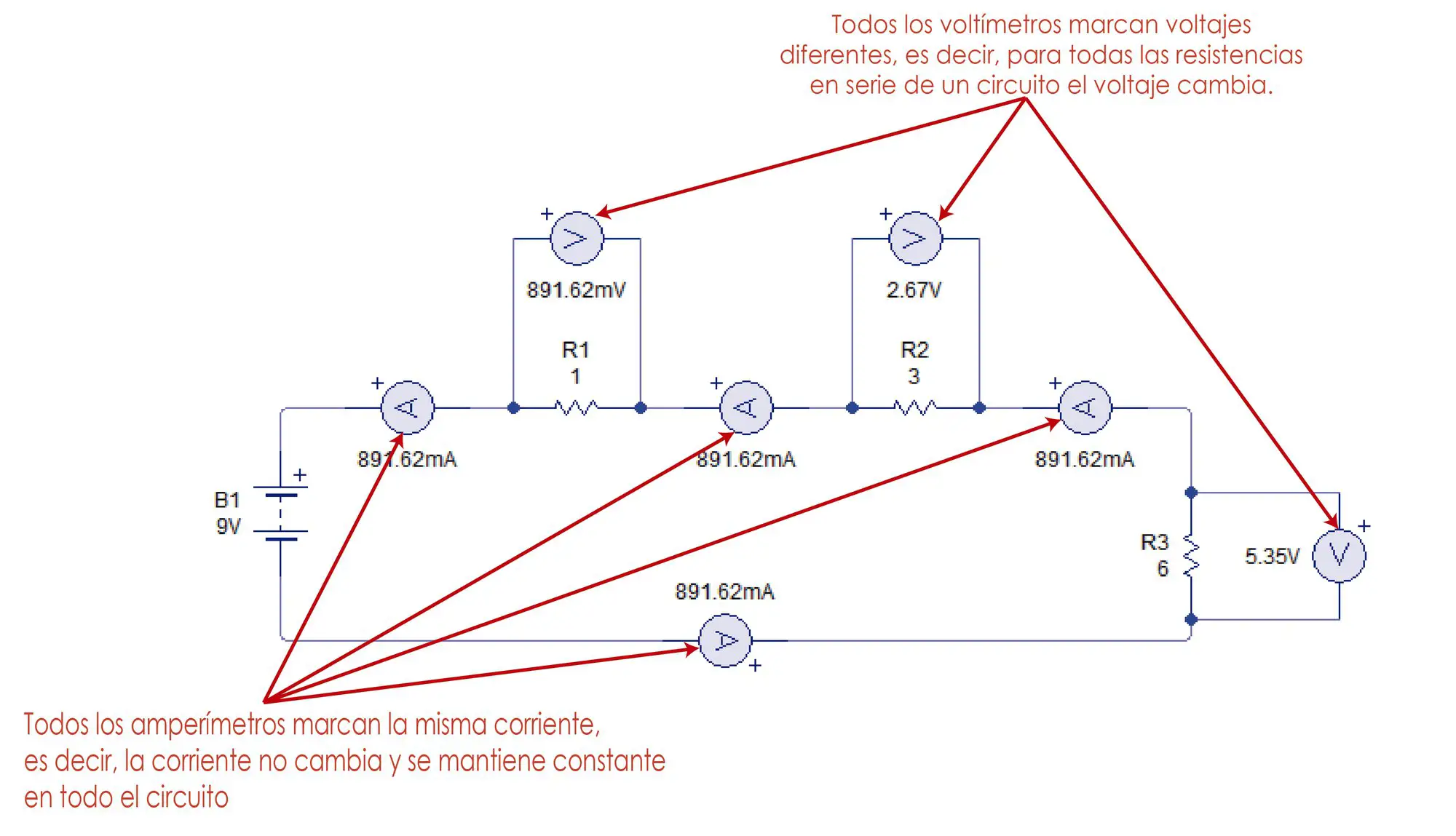
- Cuando las resistencias están en serie, la corriente es la misma para todas las resistencias, pero el voltaje varía para cada una.
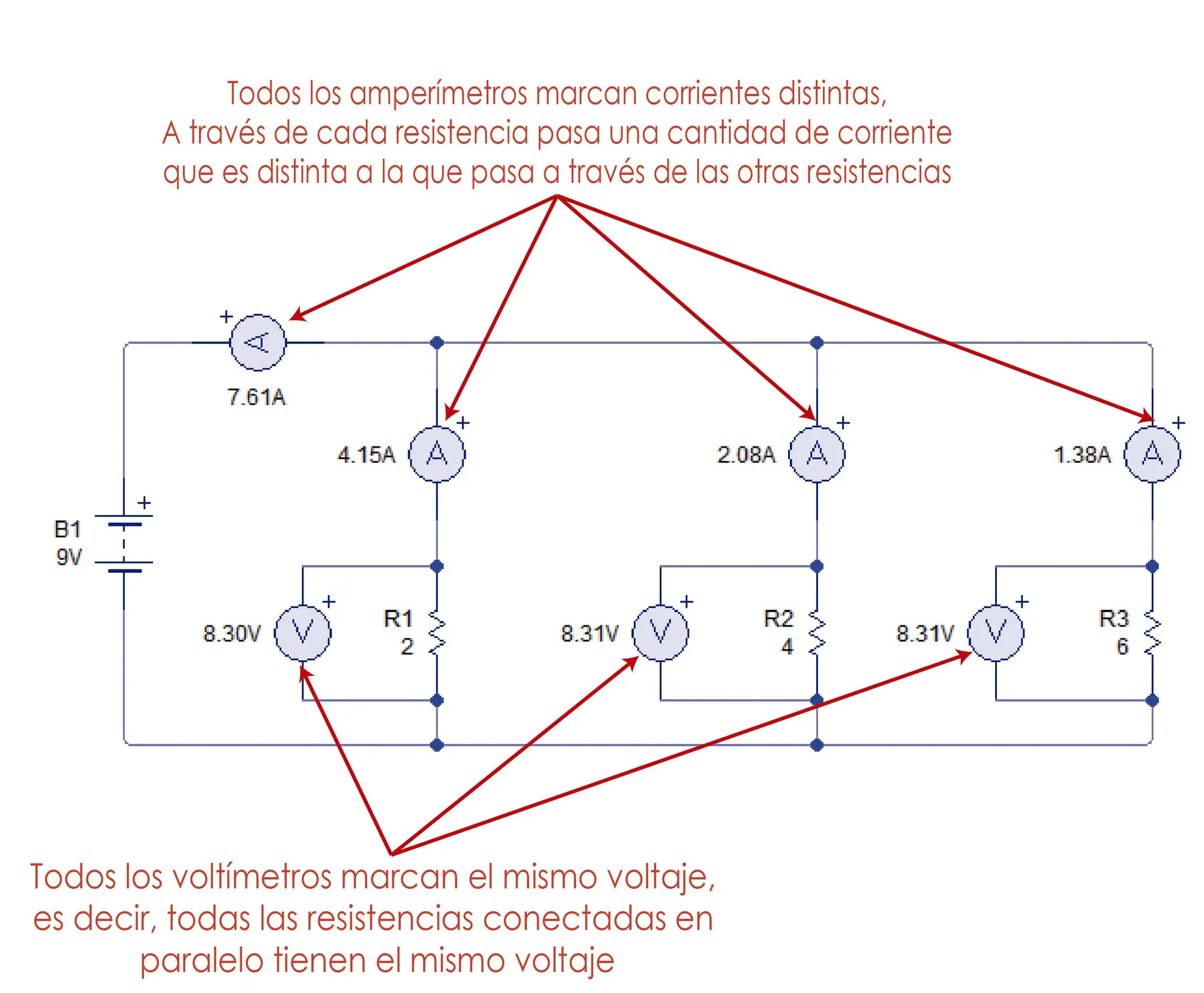
- Cuando las resistencia están en paralelo, el voltaje es el mismo para todas las resistencias pero la corriente varía para cada una.
Veamos un ejemplo:
La caída de voltaje en cada resistencia se calcula usando la Ley de Ohm. Como se sabe que la corriente para todo el circuito es la misma, en este caso 891.62 mA, entonces usamos la ecuación V = I·R para encontrar las caídas de voltaje.
Para la resistencia 1:
V = 891.62 mA x 1 Ohm = 891.62 mV
Para la resistencia 2:
V = 891.62 mA x 3 Ohm = 2.67 V
Para la resistencia 3:
V = 891.62 mA x 6 Ohm = 5.35 V
La sumatoria de todas las caídas de voltaje debe ser igual al voltaje de la fuente.
V = 891.62 mV + 2.67 V + 5.35 V = 9V.
Estas caídas de voltaje solamente se dan si las resistencias están en serie. Si las resistencias están en paralelo, entonces el voltaje será diferente y la corriente cambiará para cada resistencia. Veamos:
La suma de las corrientes que pasa a través de cada resistor es igual a la corriente que sale de la fuente. La corriente que sale de la fuente para este caso es 7.61 amperios.
Sumando 4.15 + 2.08 + 1.38 se obtiene los 7.61 amperios. La experiencia nos dice que la corriente se divide en los 3 diferentes caminos según el porcentaje de la conductancia total que se ubique en cada camino.
¿Qué quiere decir esto?
La conductancia total se obtiene sumando los inversos de cada resistencia, es decir:
Ahora se procede a calcular que porcentaje representa cada conductancia con respecto a la conductancia total.
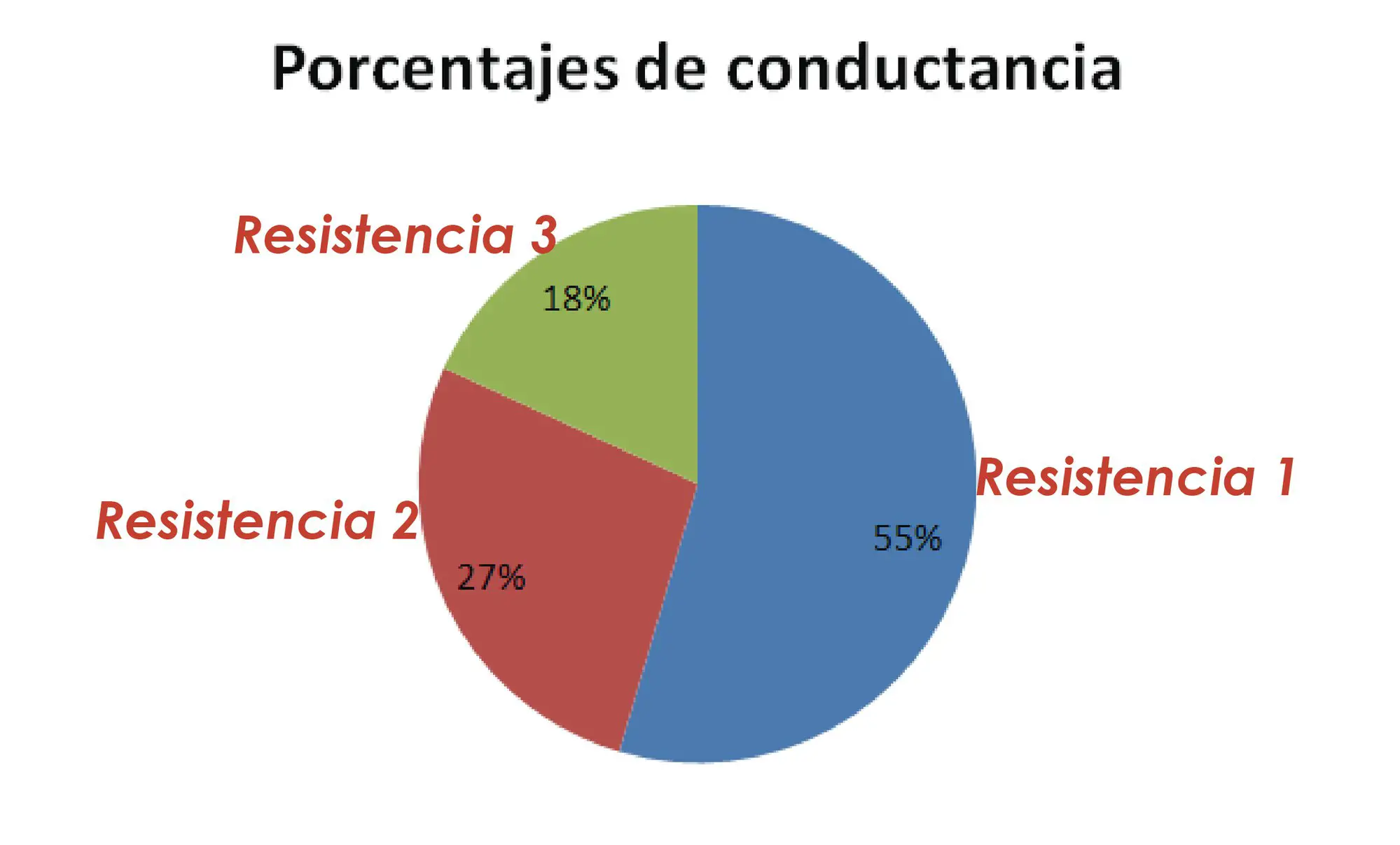
Esto quiere decir que el 55% de la conductancia pertenece a la resistencia 1 (de 2 Ohm); el 27% de la conductancia pertenece a la resistencia 2 (de 4 Ohm) y el 18% de la conductancia pertenece a la resistencia 3 (de 6 Ohm).
Esto tiene mucho sentido ya que la mayor porción de la conductancia está en la resistencia de menor valor, es decir, a través de la resistencia de 2 Ohm es por donde la corriente tiene menos dificultad al pasar y es pero ahí por donde pasará la mayor cantidad de corriente.
Ahora, utilizando estos mismos porcentajes podemos averiguar como se va a dividir la corriente total del circuito, o sea la corriente que sale de la fuente. La corriente total, como y dijimos, es 7.61 amperios. Por la resistencia 1 pasará el 55% de esa corriente. Buscamos ese 55%:
- I = 7.61 A x 0.55 = 4.19 A
Hacemos lo mismo para las otras resistencias:
- I = 7.61 x 0.27 = 2.05 A
- I = 7.61 x 0.18 = 1.37 A
Como vemos, los valores no son exactamente iguales a los de la imagen (4.15, 2.08 y 1.38). Varían unos cuantos décimos. Esto se debe a la presencia de los amperímetros en el circuito que causan una pequeña disminución. De todas maneras esa pequeña variación no la tomamos en cuenta por ser muy pequeña. Pero hemos planteado el concepto de que en un circuito en paralelo la corriente se divide de manera porcentual según la conductancia que halla en cada uno de los caminos.
Para divisor de corriente y divisor de voltaje hay algunas fórmulas que se usan en los estudios de ingeniería, pero no es nuestra intención enseñar circuitos sino que el lector pueda comprender la Ley de Ohm y saber como se comporta la corriente en los circuitos en serie y en los circuitos en paralelo.
En los siguientes enlaces se encuentran métodos para resolver circuitos eléctricos, los cuales utilizan la Ley de Ohm:
- Ley de los voltajes de Kirchhoff: Método de Mallas
- Ley de las corrientes de Kirchhoff: Método de nodos
- Leyes de Kirchhoff: El método Zbus
Espero que encuentren valor en el contenido que he preparado para ustedes. Estoy convencido de que la información proporcionada será de gran utilidad. Me encantaría escuchar sus comentarios, opiniones o sugerencias para seguir mejorando. ¡Gracias por leer y quedo a la espera de sus comentarios!


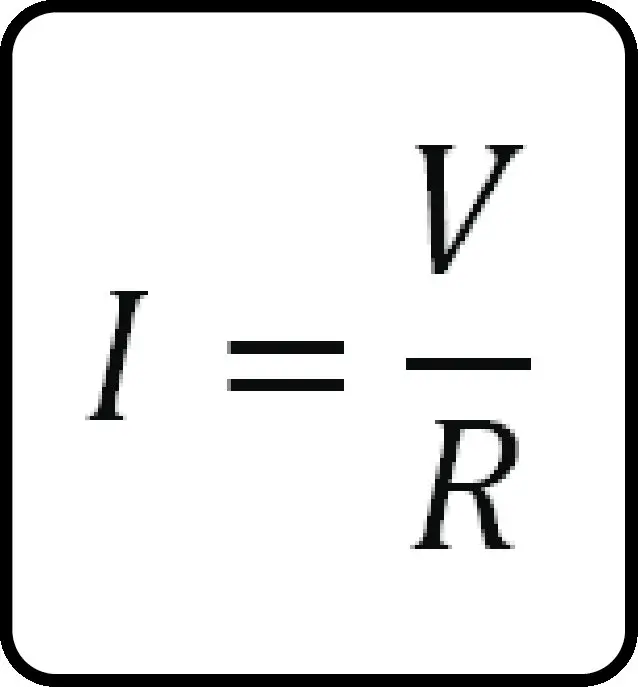
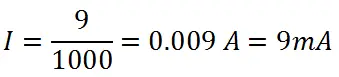
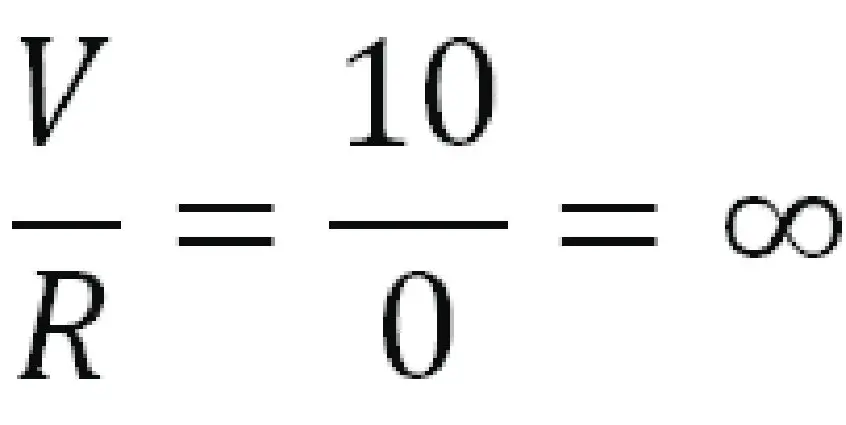


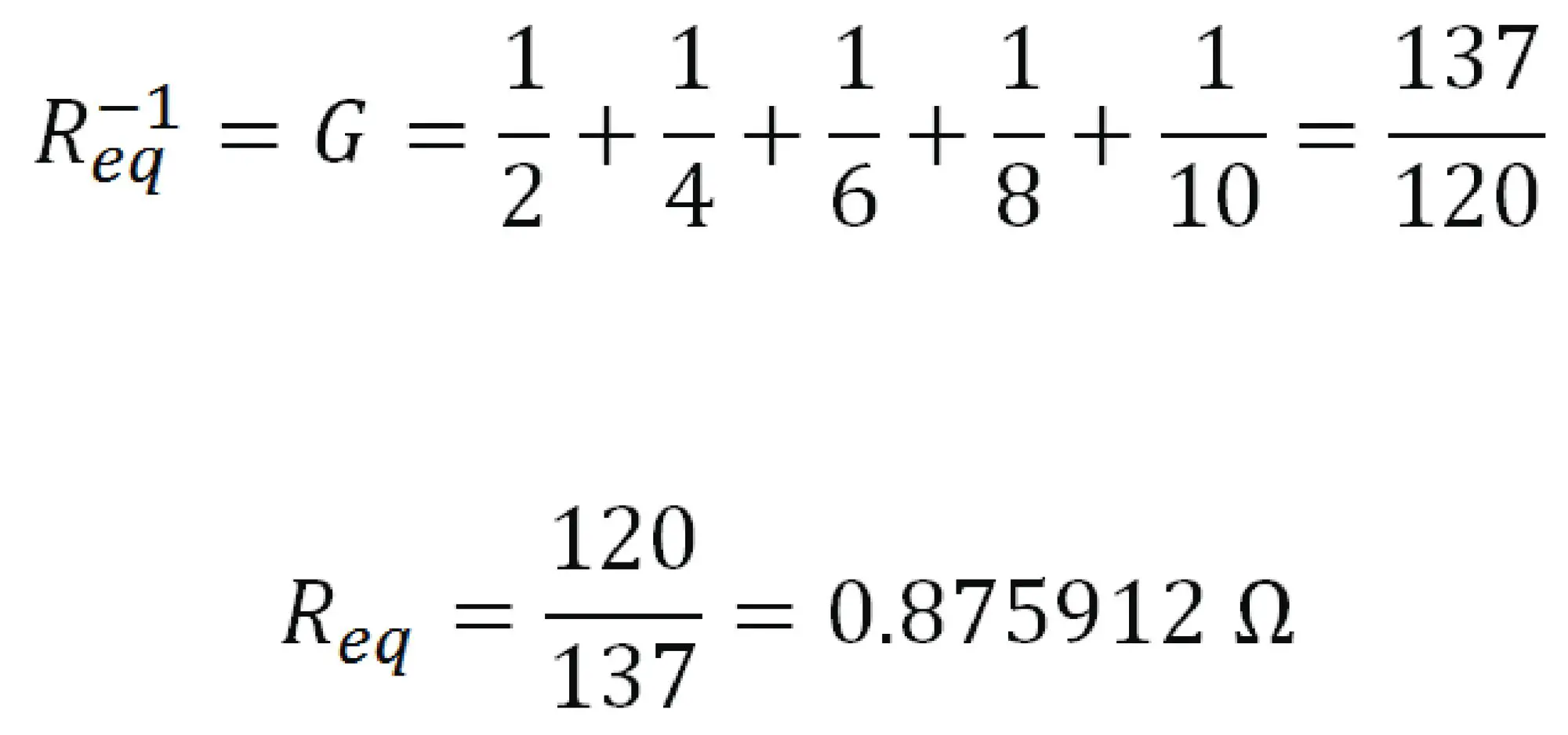
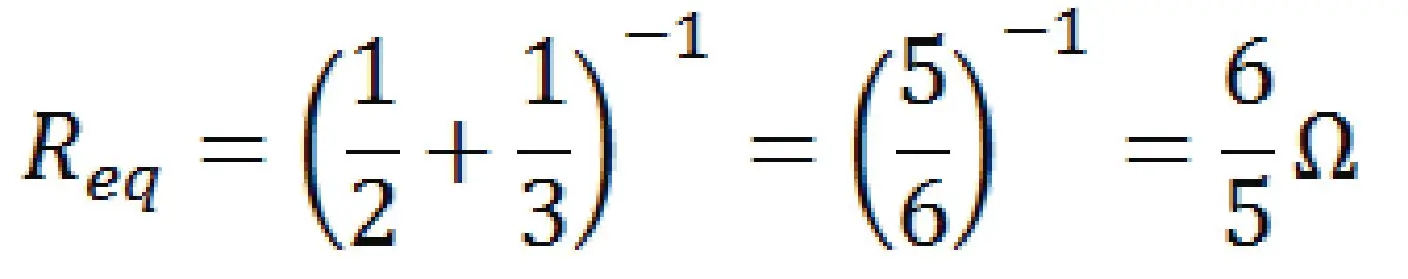
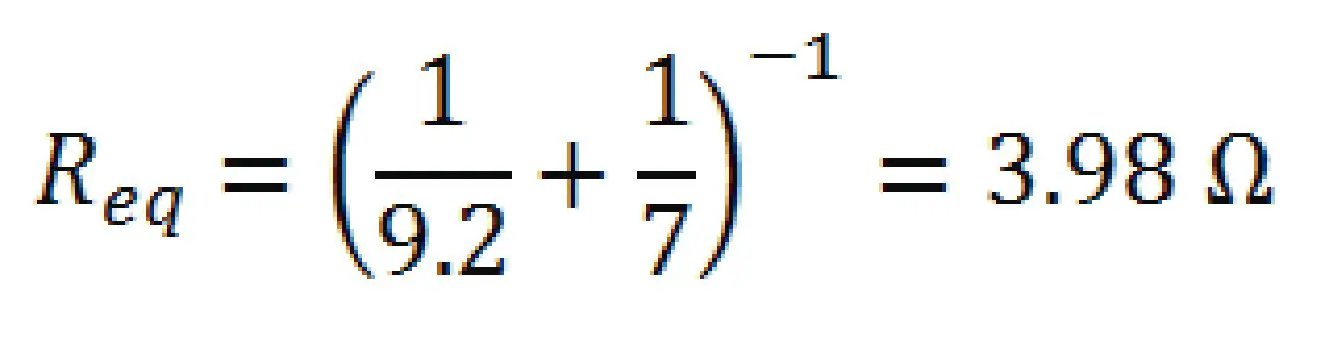
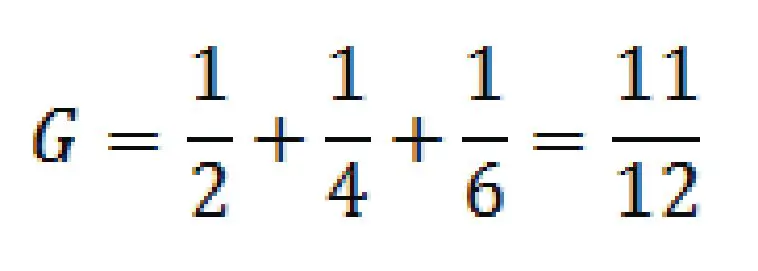










Reblogueó esto en Reparar y aprender – IFTPH –.
Mejor explicacion que he visto sobre el tema.. muchas gracias
Muchas gracias por los buenos comentarios
excelente , esta muy buena la información y la explicación
grACIAS