Como lo prometido es deuda. Después de varias semanas de trabajo, he podido terminar la solución formal al problema de circuitos a través de frecuencia compleja que compartí con ustedes hace algunas semanas. La realización del mismo fue una actividad totalmente divertidad ya que uno como tutor, siempre desea que sus estudiantes capten la mayor información posible y pues, crear una solución que abarque eso no es tan fácil como pensaba. Así que para los interesados, les recomiendo que no duden en leer la solución.
En la teoría de circuitos muchos problemas se pueden analizar por varios métodos, uno de ellos es el de frecuencia compleja. A pesar que sólo se limita a funciones de entrada: continuas, senoidales, exponenciales y senoidales amortiguadas, se debe admitir que la solución del circuito por este método es muy elegante en el plano complejo debido al uso de los números complejos.
Pues una de las ventajas de este método radica en que si el circuito es lineal; es decir, se le puede aplicar superposición. Entonces podremos trabajar más rápido en casos donde las fuentes son suma de funciones como en este caso.
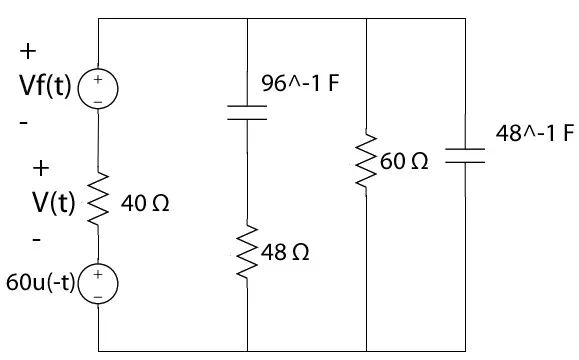
El planteamiento del problema es el siguiente: «Encontrar el voltaje en la resistencia de 40 Ω que se indica en el circuito siguiente, donde 
.
En este problema quiero indicar que se aplica bastante los conceptos básicos de circuitos aprendidos en cursos previos, así que por lo tanto si usted considera que necesita dar un repaso de esos conceptos, hágalo… porque los va a necesitar.
Bien, lo primero que debemos hacer es observar si hay interruptores, o funciones escalones que nos indicará si el circuito sufrirá cambios bruscos -algunas fuentes se pueden apagar, otras se pueden encender-. En este caso vemos que hay cambios para 
. Vemos que antes de 
se encuentra una fuente constante de 
, y en 
se enciende una fuente representada como: 
.
Esto nos indica que debemos analizar nuestro circuito en dos intervalos distintos:
Para 
y luego 
Para los capacitores se comportan como circuitos abiertos ya que no hay cambio de voltaje en el tiempo, debido a que la fuente es constante, y si hubieran bobinas, entonces ellas se comportarían como cortos circuitos.{rokbox thumb=|http://www.clase911.com/C911/images/problems/complexe_frequence/complexf_1.jpg|}http://www.clase911.com/C911/images/problems/complexe_frequence/complexf_1.jpg{/rokbox} En este caso, podemos calcular directamente el voltaje que se nos pide en la resistencia de 40 Ω. Este voltaje lo podemos encontrar con un simple divisor de voltaje: 
.Ahora, el otro punto importante es, debido a que los capacitores no aceptan un cambio brusco de voltaje, y cuando sucede un cambio brusco, ellos no pueden cambiar su voltaje bruscamente. Debido a esto debemos hallar cuánto vale el voltaje en cada capacitor justo antes de cero, el cual denotaré como: 
, cabe resaltar que este valor de voltaje que tendrá el capacitor será el mismo justo después de cero, es decir: 
. Para aquellos interesados en la parte matemática, es como si se tratará de evaluar el límite del voltaje en el capacitor cuando el tiempo tiende a cero de manera bilateral, es decir, cuando se acerca por la izquierda y por la derecha de cero. Entonces, podemos calcular los voltajes de los dos capacitores: 
que resulta obvio debido a que por la resistencia de 48 Ω no pasa corriente, por lo tanto el voltaje que hay en los extremos del capacitor uno es igual al voltaje del capacitor dos. Es importante señalar, que en este problema y en todos los de frecuencia compleja, usted le puede asignar la polaridad que deseé a cada capacitor , sólo que hay que guardar la misma polaridad durante todo el problema. Acabamos de encontrar que 
Estas expresiones del valor del voltaje en los capacitores justo antes y justo después del cambio brusco se llaman condiciones iniciales. Ahora que tenemos las condiciones iniciales de los capacitores, y lo que nos piden, es decir el voltaje en la resistencita de 40 Ω, podemos seguir al siguiente intervalo de tiempo: Nota: Mi profesora de circuitos, siempre nos decía, que es necesario dibujar el circuito que se ve después del cambio brusco. Esto es ¡CRUCIAL! ya que a la hora de evaluar las constantes que se obtienen de la respuesta natural, es necesario observar qué acontece en el circuito justo después de cero.{rokbox thumb=|http://www.clase911.com/C911/images/problems/complexe_frequence/complexf_2.jpg|}http://www.clase911.com/C911/images/problems/complexe_frequence/complexf_2.jpg{/rokbox}
Debemos tener en cuenta que justo después de cero, el circuito tendrá dos respuestas: una respuesta natural que es la que desaparece a medida que avanza el tiempo, y la respuesta forzada que es la que permanecerá. Entonces, ahora que estamos en el siguiente intervalo, piense un poco y observe qué le piden y en base a qué puede expresar lo que le piden. Esto al principo parece complicado ya que en problemas de fuente continua, cuando nos pedían calcular cualquier voltaje y corriente en un elemento, lo hacíamos directamente; Sin embargo, en análisis de fuente alterna a través de frecuencia compleja cuando hay bobinas y capacitores en un circuito, y se le pide un voltaje o corriente en una resistencia, es indispensable expresar el voltaje o corriente de la resistencia en función de voltaje en capacitor ó corriente en bobina. ¿Por qué? Cuando uno analiza el circuito para un tiempo mayor o igual a cero, las únicas cosas que uno conoce en el circuito para 
son los voltajes en los capacitores ya que estos últimos se opnen a cambios bruscos de voltaje. Por ende al inicio de este intervalo ellos tendrán el mismo voltaje que tenían justo antes de producir el cambio brusco en el circuito En cambio, las resistencias pueden cambiar bruscamente de voltaje o corriente en función del tiempo. Por lo tanto, trate de expresar el voltaje de la resistencia de 40 Ω en función del voltaje en capacitor, así a la hora de evaluar las constantes de la respuesta natural, usted podrá obtener los valores correspondientes ya que se basa en las condiciones iniciales de bobina o capacitor. Si usted es observador, puede intuir que recorriendo la malla externa se encuentra que 
De esta manera planteando en función de qué voy a expresar mi voltaje de la resistencia. Fíjese que he expresado el voltaje en función únicamente de la fuente de voltaje de excitación que se aplica después de cero, y el voltaje del capacitor. Esto me indica que únicamente me preocuparé por calcular el voltaje en el capacitor dos, y luego restar el voltaje de la fuente.
Pasamos ahora nuestro circuito al dominio s, y trabajamos con fasores e impedancias. En este caso quizás se pueda aplicar, quizás no. Pero existe muchas veces que en problemas de este tipo, es mejor calcular primero la respuesta natural. ¿Por qué? Debido a que cuando se le pide algún voltaje o corriente en cualquier elemento, se utiliza el cálculo de la impedancia o admitancia vista desde la fuente que usted apagó cuando se calcula la respuesta natural. Entonces yo preferiré primero calcular la respuesta natural. En este caso, apago todas las fuentes independientes ya sea de voltaje o corriente, en este caso sólo de voltaje, y determinaré la impedancia o admitancia vista desde la fuente que yo apagué. Recuerde que si usted apaga una fuente de voltaje ella es un corto, y si apaga una fuente de corriente ella es un circuito abierto. Como yo apagué una fuente de voltaje, buscaré los ceros de la impedancia.
{rokbox thumb=|http://www.clase911.com/C911/images/problems/complexe_frequence/complexf_3.jpg|}http://www.clase911.com/C911/images/problems/complexe_frequence/complexf_3.jpg{/rokbox}
En este momento entonces observo mi circuito y puedo decir que la impedancia que mira la fuente de voltaje es: 
Por lo tanto, la impedancaia que ve la fuente es:
Donde se demuestra que los ceros de esta impedancia son: -4 y -1
Observamos entonces que nuestra respuesta natural es la suma de dos exponenciales decrecientes, es decir que a medida que avanza el tiempo, ellas se hacen cero. Y ahora estamos listos para calcular nuestra respuesta forzada.
En este caso, hallamos el voltaje en el capacitor dos: 
donde 
es la corriente que pasa por el capacitor. Esta corriente, la podemos encontrar fácilmente si hacemos una transformación de fuente a paralelo en la primera rama del circuito y luego, por divisor de corriente encontrar la Teniendo en cuenta que 
{rokbox thumb=|http://www.clase911.com/C911/images/problems/complexe_frequence/complexf_4.jpg|}http://www.clase911.com/C911/images/problems/complexe_frequence/complexf_4.jpg{/rokbox} {rokbox thumb=|http://www.clase911.com/C911/images/problems/complexe_frequence/complexf_5.jpg|}http://www.clase911.com/C911/images/problems/complexe_frequence/complexf_5.jpg{/rokbox}
Después de algunas manipulaciones matemáticas, encontramos que 
, entonces: 
Ahora podemos calcular por superposición, la respuesta que dará cada término de la fuente de excitación:
Teniendo así:
Procedemos ahora a evaluar esta función de voltaje en 
Recordando que el voltaje del capacitor dos en es igual a la condición inicial encontrada:
teniendo nuestra primera ecuación.
Ahora nos faltaría una segunda ecuación. ¿Dónde la encontramos? Pues tendríamos que derivar la función del voltaje del capacitor dos. En donde la derivada del voltaje del capacitor viene a ser realmente la corriente justo en 
del capacitor divido entre el valor del capacitor, visto de manera matemática:
Para encontrar el valor de 
nos iremos a nuestro circuito original justo después de cero, ¡SÍ! Por eso es tan importante dibujar el circuito que queda en Aquí reemplazaremos los valores que tenemos en cero, y valorizaremos la fuente de exitación en cero, teniendo así valores únicamente constantes en nuestro circuito.
{rokbox thumb=|http://www.clase911.com/C911/images/problems/complexe_frequence/complexf_6.jpg|}http://www.clase911.com/C911/images/problems/complexe_frequence/complexf_6.jpg{/rokbox}
Dejaré que ustedes mismos calculen el valor de la corriente en el capacitor y luego comparen sus resultados. Al final tendríamos el valor de: 
De esta manera teniendo completa nuestra segunda ecuación. Colocaré entonces nuestro sistema de ecuaciones: 
Resolviendo el sistema por el método al cual ustedes se les haga más fácil, tenemos que 
Reemplazando el valor de las constantes en nuestra ecuación final del voltaje de capacitor tendremos:
y por lo tanto el voltaje en la resistencia de 40 Ω sería el voltaje del capacitor dos menos el de la fuente.
Les dejo la tarea que expresen el voltaje en su mínima expresión. Ahora, deténgase un poco y piense de qué manera puede usted corrobar que su solución ha sido la correcta; es más: ¿Existe una manera de confirmarlo? Leeré sus comentarios e ideas. Si no entienden algo, no duden en escribir un comentario con sus dudas.
