La Ley de las Corrientes de Kirchhoff, una de las principales leyes de la electricidad utilizada en el análisis de circuitos eléctricos y electrónicos. En este post les voy a explicar como se encuentra las corrientes y los voltajes en un circuito haciendo análisis nodal con la Ley de las Corrientes de Kirchhoff. Lo primero que se necesita para este análisis es conocer qué es un nodo.
¿Qué es un nodo?
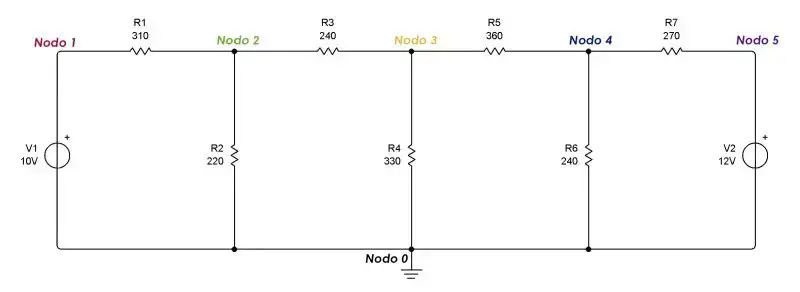 En un circuito eléctrico, un nodo es un punto donde se cruzan dos o más elementos de circuitos, sea una fuente de voltaje o corriente, resistencias, capacitores, inductores, etc. Para explicar este método usaremos el mismo circuito que usamos en mi anterio post:
En un circuito eléctrico, un nodo es un punto donde se cruzan dos o más elementos de circuitos, sea una fuente de voltaje o corriente, resistencias, capacitores, inductores, etc. Para explicar este método usaremos el mismo circuito que usamos en mi anterio post:
En la figura de la parte superior se pueden apreciar los nodos que hemos identificado. Entre la fuente de la izquierda y la resistencia 1 hay un nodo. Lo mismo entre las resistencias R1, R2 y R3. Entre las resistencias R3, R4 y R5. Entre las resistencias R5, R6 y R7. Entre la fuente de la derecha y la resistencia R7. Todos estos elementos van conectados a un nodo en común, el nodo cero, donde se coloca tierra.
El propósito del método de nodos es encontrar el voltaje entre todos los nodos y tierra. La diferencia de potencial se produce debido a las caídas de voltaje que le permiten a La Ley de Ohm cumplirse. Pero, en los nodos formados entre resistencias y fuentes ya conocemos el voltaje, es decir, el voltaje de la fuente. En el nodo común, el aterrizado, el voltaje es cero. 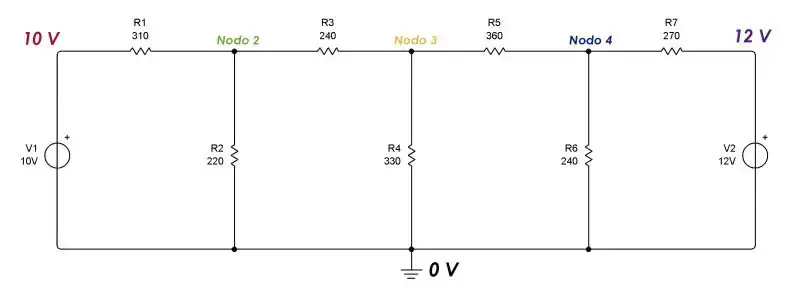 Para encontrar los voltajes en los nodos 2, 3 y 4 utilizamos el principio fundamental de la Ley de las Corrientes de Kirchhoff: la sumatoria de las corrientes que entran a un nodo es igual a la sumatoria de las corrientes que salen del nodo.
Para encontrar los voltajes en los nodos 2, 3 y 4 utilizamos el principio fundamental de la Ley de las Corrientes de Kirchhoff: la sumatoria de las corrientes que entran a un nodo es igual a la sumatoria de las corrientes que salen del nodo. ![]() Esto no es más que una extensión del Principio de la Conservación de la Energía que es lo que en sí le da su origen a la Ley de Las Corrientes de Kirchhoff. Para saber las corrientes que entran o salen de un nodo, utilizamos la Ley de Ohm. Según la Ley de Ohm, la corriente que pasa por una resistencia es igual a la diferencia de potencial entre la resistividad.
Esto no es más que una extensión del Principio de la Conservación de la Energía que es lo que en sí le da su origen a la Ley de Las Corrientes de Kirchhoff. Para saber las corrientes que entran o salen de un nodo, utilizamos la Ley de Ohm. Según la Ley de Ohm, la corriente que pasa por una resistencia es igual a la diferencia de potencial entre la resistividad.
I=V/R
La diferencia de potencial a la que está sometida una resistencia es igual al voltaje antes de la resistencia menos el voltaje después de la resistencia. Con esto construiremos nuestras ecuaciones para cada nodo. Necesitamos primero escoger el sentido de las corrientes tomando en cuenta que cuando hay una fuente de voltaje la corriente sale del positivo de la fuente. Si no hay una fuente se asume que todas las corrientes fluyen de izquierda a derecha y de arriba hacia abajo. Dicho esto tenemos: 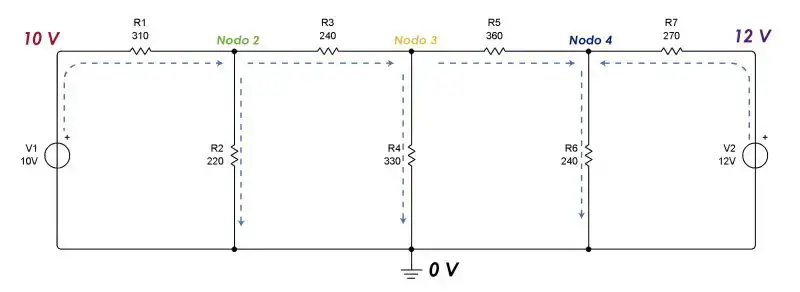 Debemos tener en cuenta que la corriente va de un área de mayor potencial a un área de menor potencial. [youtube=http://www.youtube.com/watch?v=Mk_l5OCFLK8] Al escoger el sentido de la corriente como lo hemos hecho, es decir, de izquierda a derecha asumimos que los potenciales disminuyen de izquierda a derecha. Ahora procedemos a analizar nodo por nodo.
Debemos tener en cuenta que la corriente va de un área de mayor potencial a un área de menor potencial. [youtube=http://www.youtube.com/watch?v=Mk_l5OCFLK8] Al escoger el sentido de la corriente como lo hemos hecho, es decir, de izquierda a derecha asumimos que los potenciales disminuyen de izquierda a derecha. Ahora procedemos a analizar nodo por nodo.
Nodo 2
Como en el Nodo 1 ya conocemos el coltaje (voltaje de la fuente, voltios) procedemos a analizar el nodo 2. 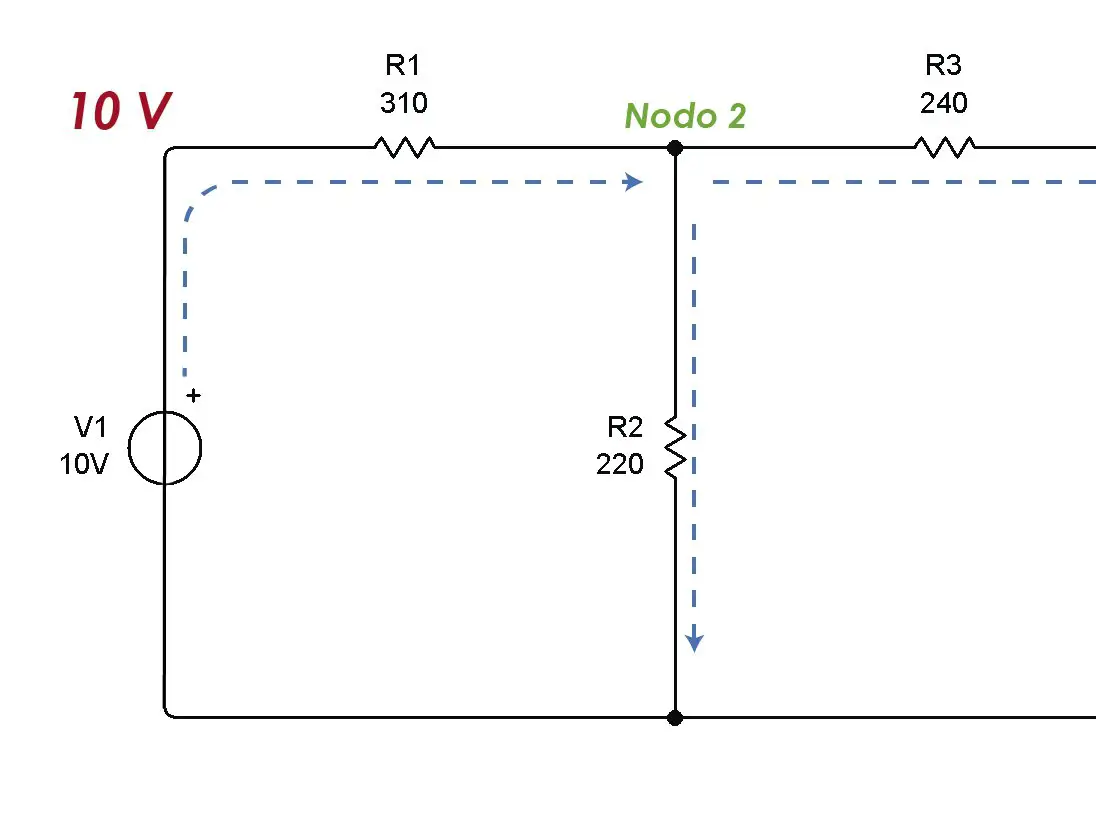 La única corriente que entra al nodo es la que viene de la fuente. La corriente que baja por R2 y por R3 salen del nodo.
La única corriente que entra al nodo es la que viene de la fuente. La corriente que baja por R2 y por R3 salen del nodo. 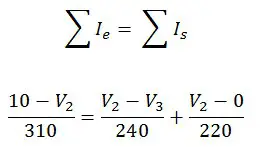 Vemos que la corriente que entra es la diferencia de voltajes entre la resistencia R1. Se asume que los 10 voltios de la fuente es mayor al voltaje en el nodo 2 ya que se produce una caída de voltaje en la resistencia. Las corrientes que salen serán la corriente que va del nodo 2 al nodo 3 y las que van del nodo 2 a tierra. Se asume que el voltaje 2 es mayor que el voltaje en el nodo 3. El voltaje en tierra es cero voltios. Al final la ecuación es la siguiente:
Vemos que la corriente que entra es la diferencia de voltajes entre la resistencia R1. Se asume que los 10 voltios de la fuente es mayor al voltaje en el nodo 2 ya que se produce una caída de voltaje en la resistencia. Las corrientes que salen serán la corriente que va del nodo 2 al nodo 3 y las que van del nodo 2 a tierra. Se asume que el voltaje 2 es mayor que el voltaje en el nodo 3. El voltaje en tierra es cero voltios. Al final la ecuación es la siguiente: 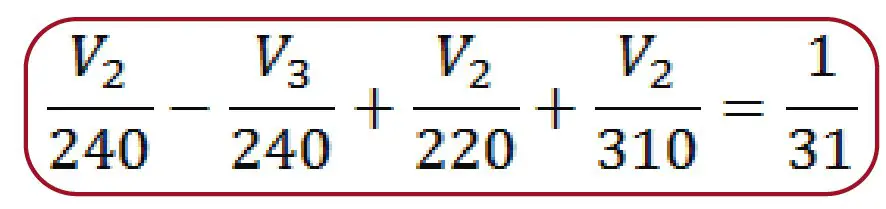 Se trata de igualar la ecuación a cualquier término libre que tengamos. En este caso, el voltaje de la fuente.
Se trata de igualar la ecuación a cualquier término libre que tengamos. En este caso, el voltaje de la fuente.
Nodo 3
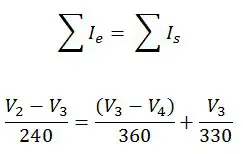 Las corrientes que tomamos como salientes en un nodo deben ser tomadas como entrantes en el próximo nodo. La ecuación quedaría de esta forma.
Las corrientes que tomamos como salientes en un nodo deben ser tomadas como entrantes en el próximo nodo. La ecuación quedaría de esta forma.  Nodo 4
Nodo 4
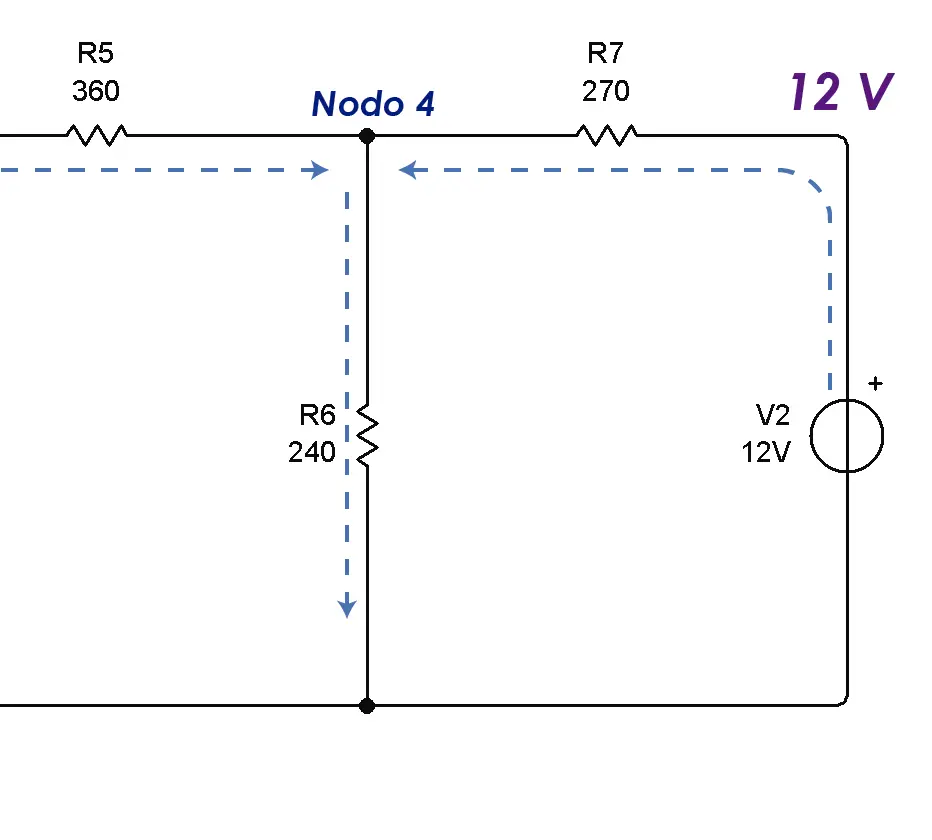
Al nodo 4 entran 2 corrientes y sale una. 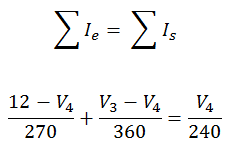 Una vez más debemos recordar que la corriente sale del positivo de la fuente. El sentido de las flechas indica cuales corrientes entran y cuales salen del nodo.
Una vez más debemos recordar que la corriente sale del positivo de la fuente. El sentido de las flechas indica cuales corrientes entran y cuales salen del nodo. 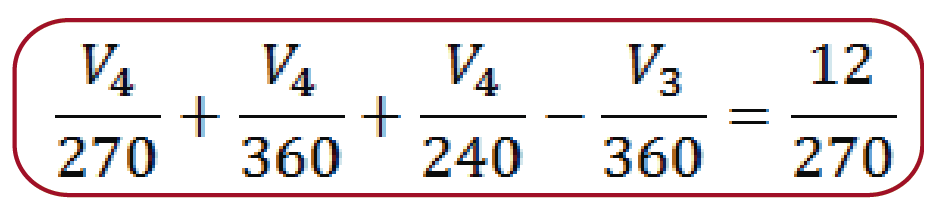 Con esto hemos establecido todas las ecuaciones para los 3 nodos que estamos analizando.
Con esto hemos establecido todas las ecuaciones para los 3 nodos que estamos analizando.
Resolviendo el sistema de ecuaciones lineales
Siempre que se trabaja con la Ley de las Corrientes de Kirchhoff aparece un sistema de ecuaciones lineales. Luego de establecidas las ecuaciones, se procede a resolver el mismo. Se puede usare cualquier método (reducción, sustitución, determinantes, etc). Yo prefiero utlizar el método de Gauss-Jordan. 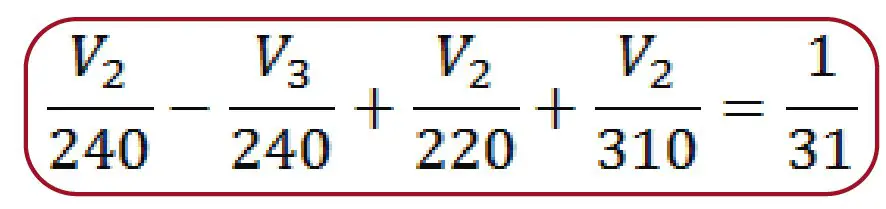

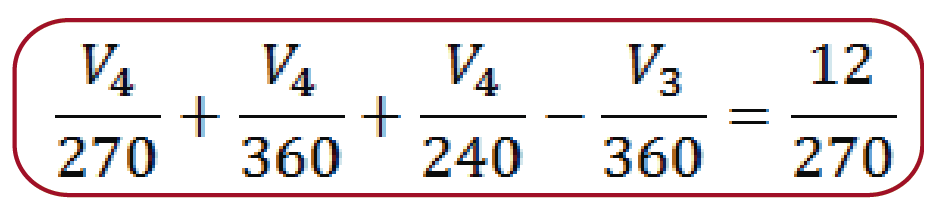 Se lleva todo a una matriz.
Se lleva todo a una matriz. 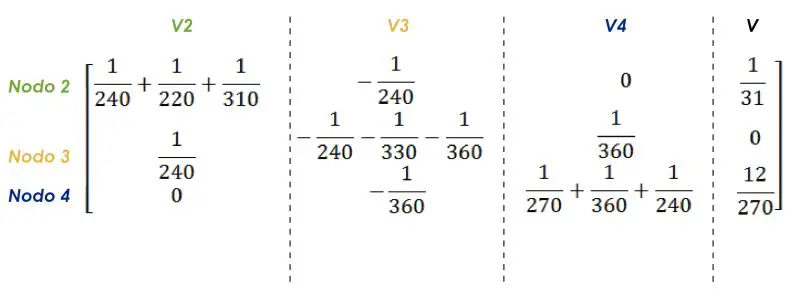 Ahora podemos escoger cualquier método para resolver esta matriz. Yo usaré Microsoft Mathematics y posteriormente Matlab y Excel.
Ahora podemos escoger cualquier método para resolver esta matriz. Yo usaré Microsoft Mathematics y posteriormente Matlab y Excel.
Microsoft Mathematics
Insertamos una matriz nxn+1 donde n es la cantidad de nodos a analizar. 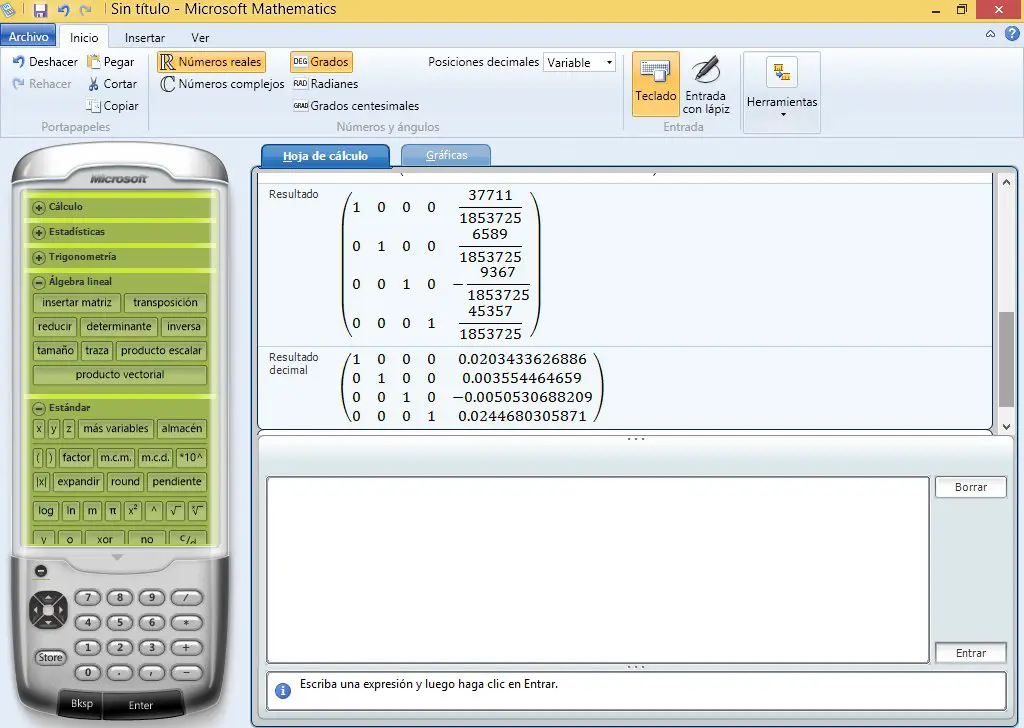
 Introducimos los datos a la matriz.
Introducimos los datos a la matriz. 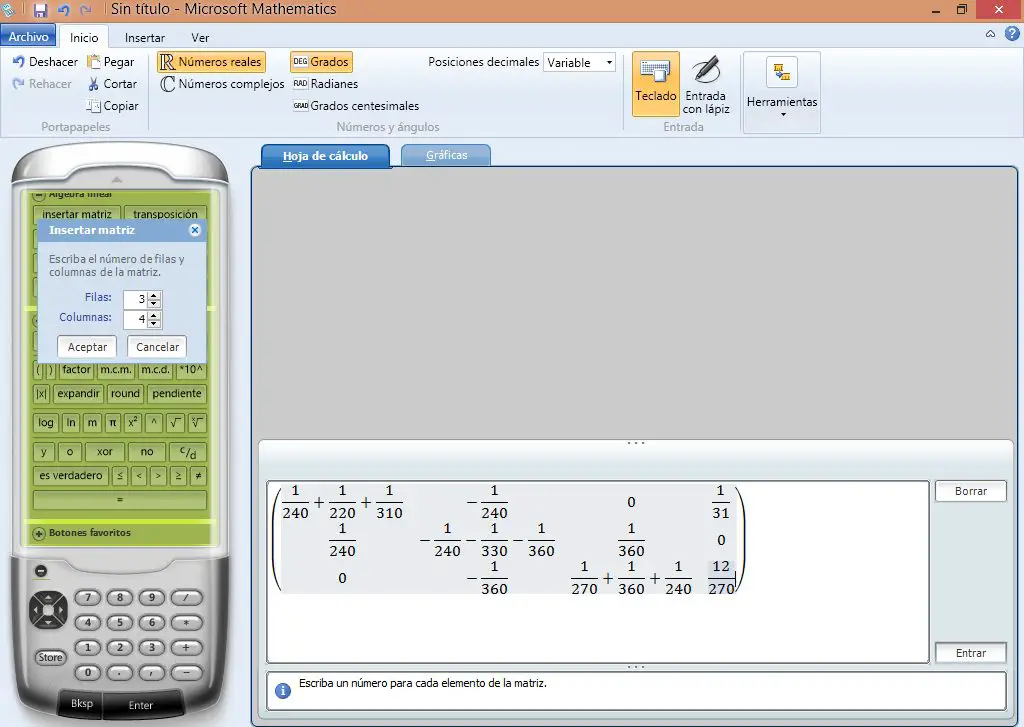 Se aplica reducción y se obtiene los resultados.
Se aplica reducción y se obtiene los resultados. 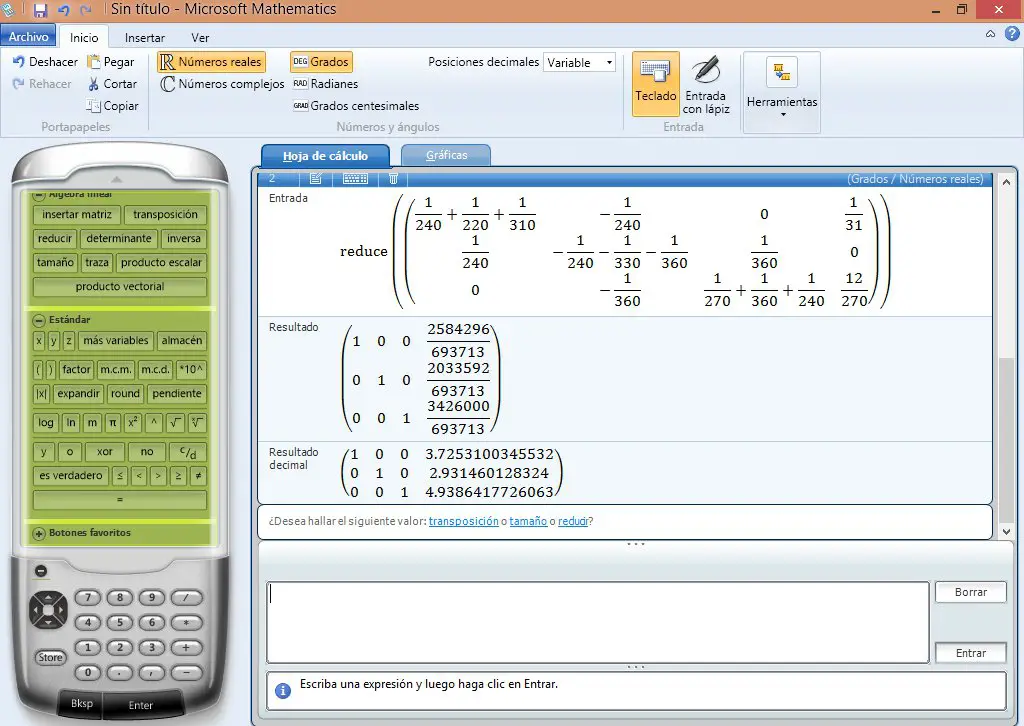 Los voltajes en los nodos 2, 3 y 4 son 3.73, 2.93 y 4.94 voltios, respectivamente. Esto lo podemos comprobar en el simulador:
Los voltajes en los nodos 2, 3 y 4 son 3.73, 2.93 y 4.94 voltios, respectivamente. Esto lo podemos comprobar en el simulador:  Se comprueba que nuestros cálculos han sido correctos.
Se comprueba que nuestros cálculos han sido correctos.
Matlab
En Matlab necesitamos declarar la matriz con nuestros datos. 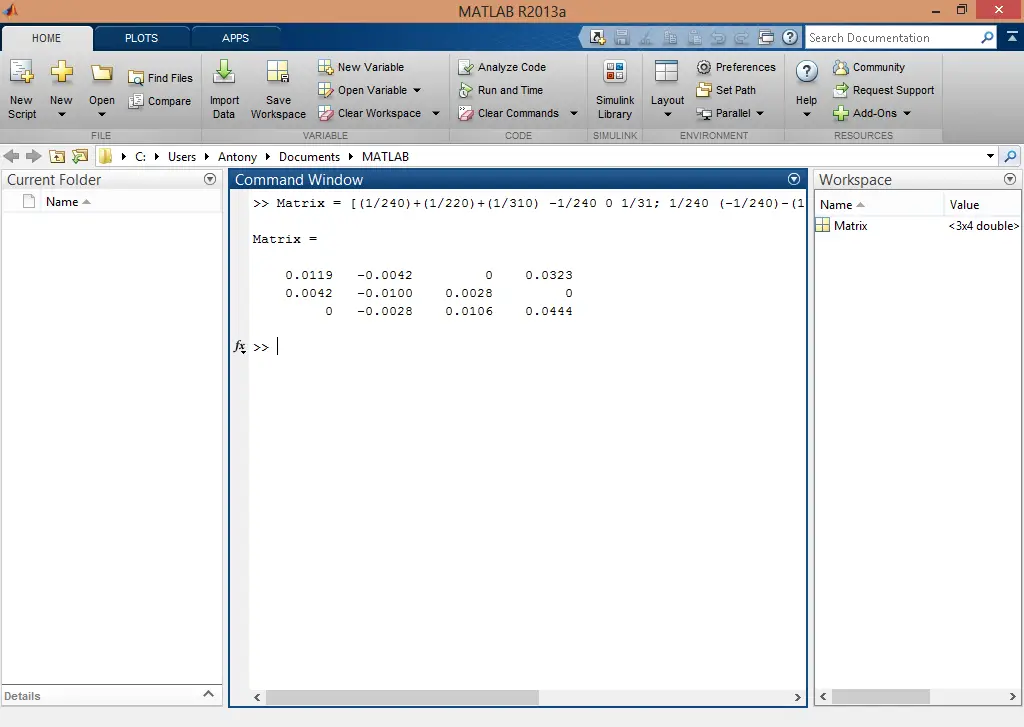 Se aplica el comando rref() para reducir la matriz.
Se aplica el comando rref() para reducir la matriz. 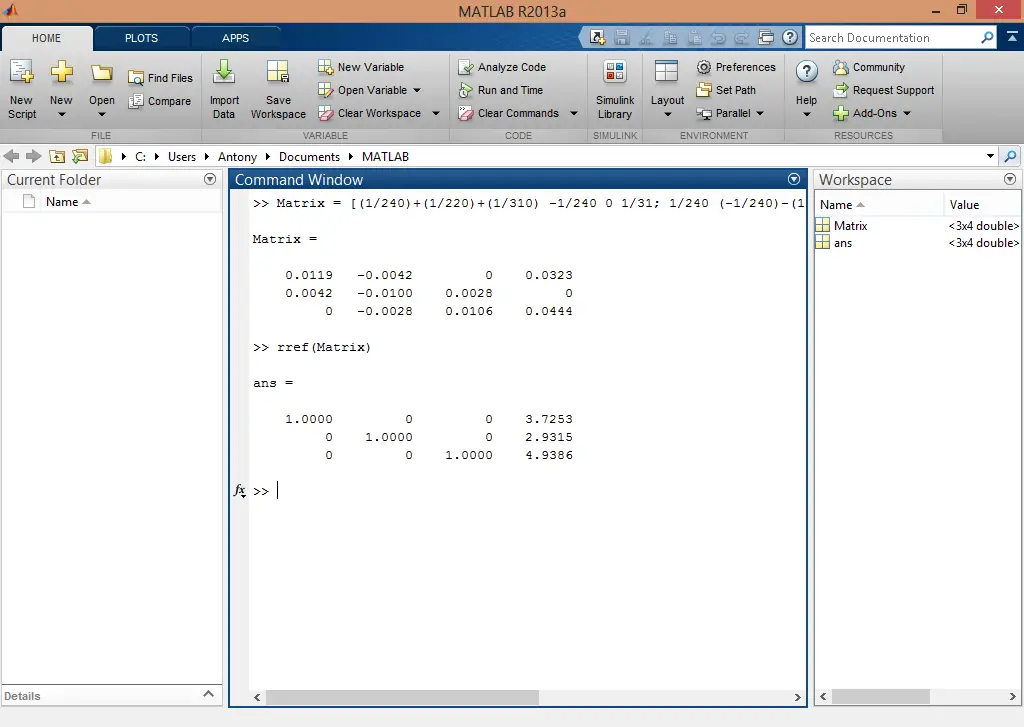
Excel
Para facilitar las cosas con Excel, es recomendable que reduzcamos la matriz a valores de fraccionarios, realizando las sumas que quedaron implícitas en nuestra matriz de ecuaciones. De esta manera nos debe quedar una matriz como esta: 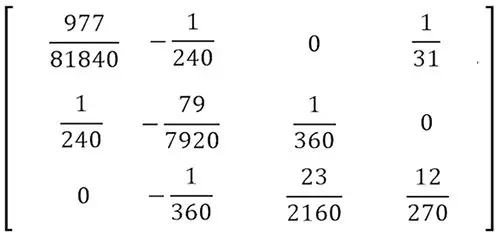 También podemos transformar estas fracciones a decimales.
También podemos transformar estas fracciones a decimales.  Una vez tengamos estos datos, es muy fácil resolver este sistema de ecuaciones utilizando Excel. Mi estimado amigo Secundino Villarreal, Ingeniero Electromecánico y docente de física en la Universidad Tecnológica de Panamá lanzó el sitio web excelparaingenieria.com en donde constantemente está publicando plantillas diseñadas en Excel. Hemos utilizado la plantilla Gauss Jordan: Ecuaciones Simultáneas 3 x 3 para resolver el sistema de ecuaciones de este ejemplo. La plantilla se encuentra disponible de forma gratuita en la web del autor. Cuando la descargamos veremos algo como esto:
Una vez tengamos estos datos, es muy fácil resolver este sistema de ecuaciones utilizando Excel. Mi estimado amigo Secundino Villarreal, Ingeniero Electromecánico y docente de física en la Universidad Tecnológica de Panamá lanzó el sitio web excelparaingenieria.com en donde constantemente está publicando plantillas diseñadas en Excel. Hemos utilizado la plantilla Gauss Jordan: Ecuaciones Simultáneas 3 x 3 para resolver el sistema de ecuaciones de este ejemplo. La plantilla se encuentra disponible de forma gratuita en la web del autor. Cuando la descargamos veremos algo como esto:  Un poco más abajo encontraremos un cuadro donde ingresamos los valores de nuestras ecuaciones. La plantilla irá calculando automáticamente las respuestas del problema al hacer la reducción de Gauss-Jordan.
Un poco más abajo encontraremos un cuadro donde ingresamos los valores de nuestras ecuaciones. La plantilla irá calculando automáticamente las respuestas del problema al hacer la reducción de Gauss-Jordan. 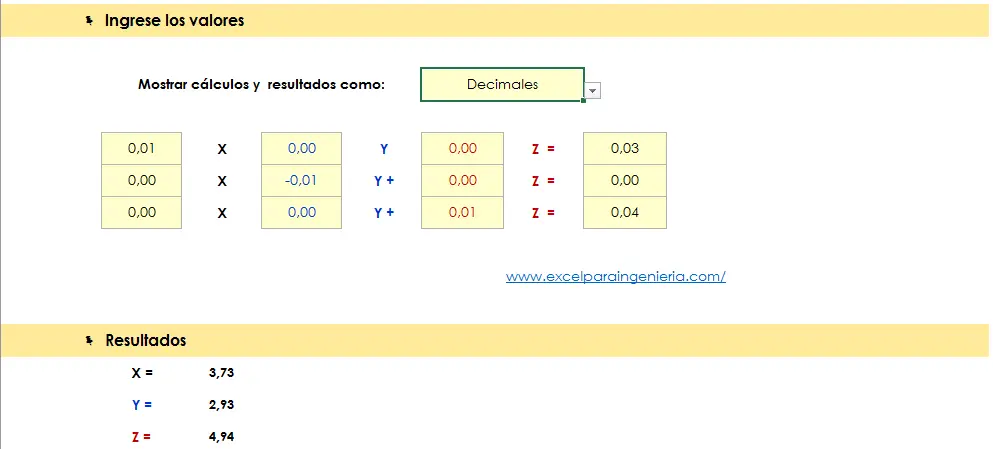
Como podemos observar, los resultados son iguales a aquellos obtenidos con Microsoft Mathematics y Matlab. En la matriz solo vemos números con dos decimales, debido a que ésta es la cantidad preestablecida por el diseñador. El usuario puede escoger la forma como desea que los datos queden visualizados, ya sea en notación científica, fracciones, decimales, etc. Como ya dijimos, la plantilla la podemos descargar desde la web del autor.
Al final el resultado es el mismo. Cuando obtenemos los voltajes en los nodos podemos calcular las corrientes de malla al saber cuanta corriente está pasando por cada resistencia en un punto determinado. En el siguiente video se muestra el proceso completo: [youtube https://www.youtube.com/watch?v=VIYnUH4KQXs]
El propósito de publicar acerca de la Ley de Las Corrientes de Kirchhoff ha sido crear una referencia para los cálculos que se realizan en los diferentes proyectos que se han presentado y se presentarán en este sitio web.
Problemas resueltos de Leyes de Kirchhoff
En Panama Hitek hemos creado una sección especial para compartir problemas resueltos de teoría de circuitos eléctricos. Los problemas resueltos poseen diferentes niveles de dificultad y han sido diseñados para evaluar conceptos en estudiantes de cursos de ingeniería eléctrica y disciplinas afines.
La Ley de las Corrientes de Kirchhoff es una herramienta esencial para el análisis de circuitos eléctricos y electrónicos. Esta ley permite encontrar los voltajes y corrientes en cada elemento de un circuito utilizando el método de nodos y aplicando la Ley de Ohm. Gracias por leer este post y espero que haya sido útil. Si tienes alguna pregunta o comentario, no dudes en dejármelo a continuación. ¡Hasta pronto!











Muchas gracias ingeniero, excelente explicacion, lo unico malo es que en los parciales no dejan sacar la calculadora para resolver las ecuaciones lineales.
Yo a mis estudiantes si los dejo usar la calculadora
si lo puede hacer una calculadora para usted debería ser extremadamente fácil. (si es que estudia ingeniería)
Creo que el análisis es esencial, fuera de eso se puede elegir el método que se desee… en mi caso me gusta usar superposición o thévenin, me ahorra tiempo y así puedo verificar resultados en Breadboard.