Simulando el problema del viajante en Java

El problema del viajante es uno de los problemas clásicos de optimización. Consiste en encontrar la ruta más corta que recorre todos los puntos de un conjunto dado de coordenadas.

En este post, vamos a presentar una aplicación en Java para simular el TSP utilizando algoritmos de permutaciones, cálculo de distancias y una interfaz gráfica de usuario (GUI) para visualizar los resultados. El objetivo es proporcionar una comprensión detallada del proceso de simulación y una guía paso a paso para aquellos interesados en implementar su propia solución del TSP en Java.

¿En qué consiste el problema del viajante?

El problema del viajante (TSP por sus siglas en inglés, Travelling Salesman Problem) es uno de los problemas de optimización más estudiados en investigación operativa y ciencias de la computación. Se trata de encontrar la ruta más corta posible que visita cada ciudad exactamente una vez y al finalizar regresa a la ciudad origen, dada una lista de ciudades y las distancias entre cada par de ellas.

Este problema fue formulado por primera vez en 1930 y es considerado un problema NP-Hard dentro de la optimización combinatoria. Aunque es computacionalmente complejo, existen métodos heurísticos y métodos exactos que permiten resolver planteamientos concretos del problema, desde cien hasta miles de ciudades.

El TSP tiene diversas aplicaciones en su formulación más simple, como la planificación, la logística y la fabricación de circuitos electrónicos. Sin embargo, al ser modificado ligeramente, también aparece como subproblema en muchos campos como la secuenciación de ADN. En esta aplicación, el concepto de “ciudad” representa, por ejemplo, clientes, puntos de soldadura o fragmentos de ADN y el concepto de “distancia” representa el tiempo de viaje o costo, o una medida de similitud entre los fragmentos de ADN.

El TSP es un problema de optimización importante y con muchas aplicaciones en distintos campos. Sin embargo, su complejidad computacional lo hace difícil de resolver de forma exacta, por lo que es necesario utilizar heurísticas y métodos aproximados para encontrar soluciones óptimas.

Complejidad computacional del TSP

El TSP es un problema de optimización combinatoria conocido como NP-Hard, lo que significa que el tiempo de ejecución para resolverlo aumenta de forma exponencial con respecto al número de ciudades involucradas. Esto se debe a que el número de posibles rutas para visitar todas las ciudades exactamente una vez y regresar a la ciudad de origen, es de n! (n factorial), donde n es el número de ciudades.

Por ejemplo, si hay 4 ciudades, el número de posibles rutas sería 4! (4x3x2x1) = 24. Si hay 5 ciudades, el número de posibles rutas sería 5! (5x4x3x2x1) = 120. Y así sucesivamente. A continuación les presento una tabla con el crecimiento exponencial de las posibles rutas que podría seguir el viajante en función de la cantidad de ciudades:

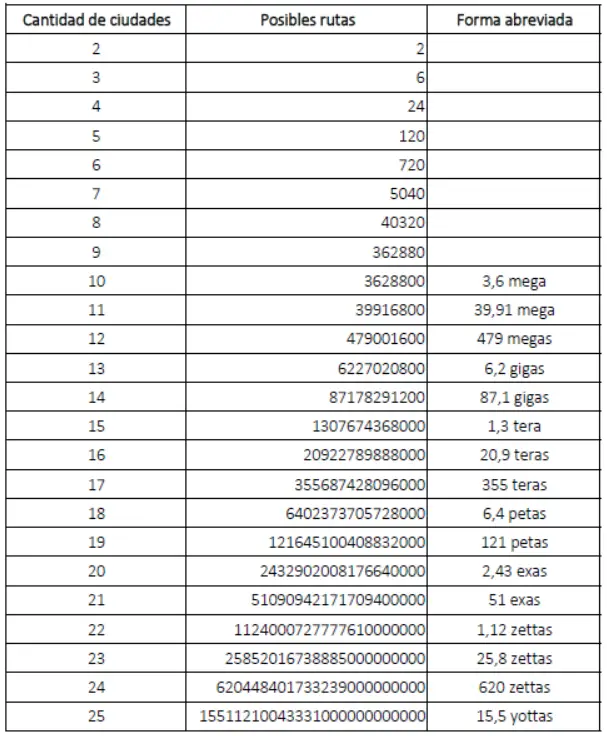
Como se puede ver, el número de posibles rutas crece de manera exponencial con el número de ciudades, lo que dificulta la resolución del problema. 25 ciudades representan 15.5 yottas de posibilidades. Eso son 15.5 cuatrillones o 15.7 septillones de posibilidades, dependiendo de si se usa la escala corta o la escala larga (la escala corta es la que usan los estadounidenses, donde 1000 millones es 1 billón).

Para poner esto en perspectiva, en nuestros días las computadoras tienen un espacio de almacenamiento en disco duro en el orden de los terabytes. Sin embargo, incluso con solo 16 ciudades, el número de combinaciones posibles alcanza los 20.9 tera-combinaciones. Si asignamos solo 1 byte a cada combinación, se necesitaría un disco duro de más de 21 terabytes (21,000 gigas) para almacenar toda la información generada, sin mencionar la cantidad de memoria RAM necesaria para abordar un problema de esta magnitud.

Para resolver el problema del vendedor viajero con un algoritmo exacto, es necesario buscar y evaluar todas las posibles rutas. Aunque esto es posible para un pequeño número de ciudades, se vuelve computacionalmente inviable para un número significativo de ciudades debido al tiempo de ejecución requerido. Por lo tanto, se utilizan heurísticas y algoritmos aproximados para resolver el problema en casos concretos con un número importante de ciudades.

Representación gráfica del problema del viajante en Java

En días recientes me he empezado a interesar por aprender algoritmos de optimización, tales como Ant Colony Optimization y Particle Swarm Optimization. Estos algoritmos permiten resolver distintos problemas de optimización, entre ellos el problema del viajante.

Con el propósito de poder probar el funcionamiento de los algoritmos de optimización decidí construir una interfaz gráfica que me permitiera representar el TSP y las posibles soluciones que se le puede dar a este problema. La interfaz es la siguiente:

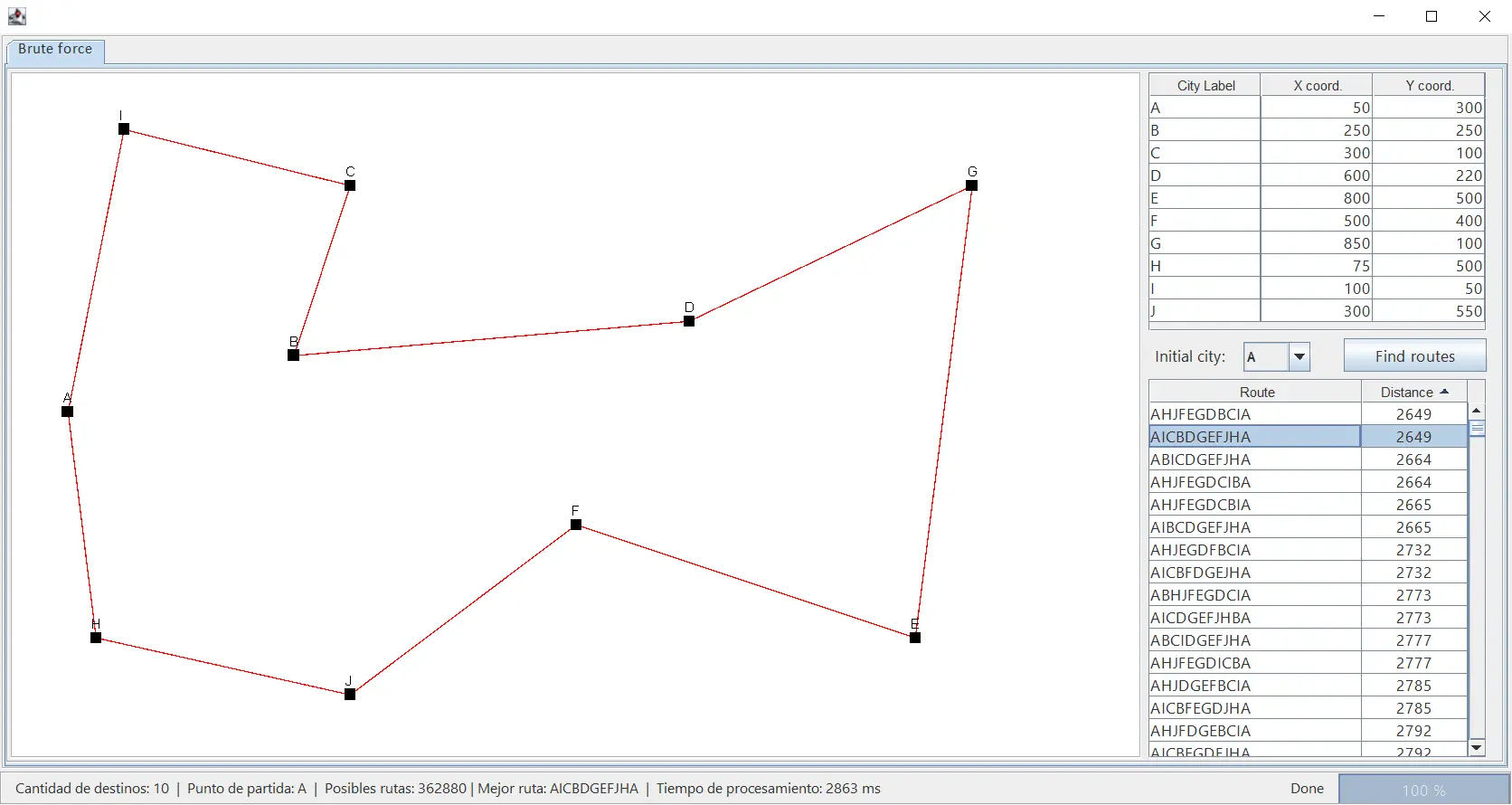
Cada uno de los cuadritos negros representa una ciudad. Las líneas rojas son las distancias entre cada ciudad. El software permite seleccionar un punto de partida y calcular todas las posibles combinaciones que permiten unir los puntos. Estas combinaciones se pueden visualizar en la tabla de la derecha, donde es posible ordenarlas en función de la distancia total.

La trayectoria descrita en la imagen representa la ruta óptima que permite recorrer todas las ciudades partiendo del punto «A». Esta interfaz también nos permite ver la peor de las rutas:

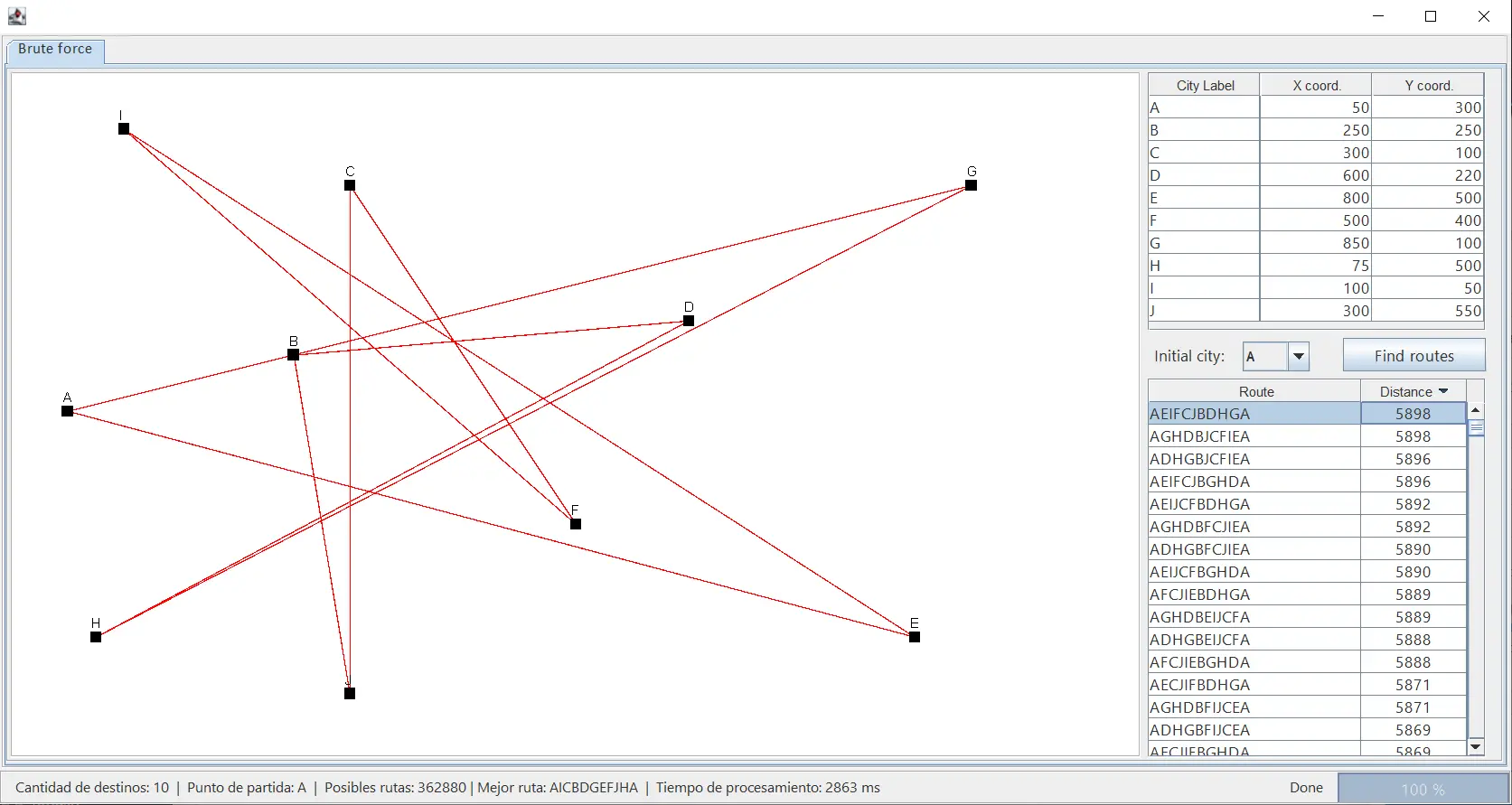
Mi idea es utilizar esta interfaz para calcular soluciones para problemas específicos por medio de «fuerza bruta», es decir, probando todas las combinaciones posibles para un conjunto de coordenadas. Luego, con las respuestas calculadas trataré de replicar los resultados coon los algoritmos de optimización, los cuales deberían ser capaces de llegar a la misma respuesta sin tener que probarlas todas.

Descripción del algoritmo

El código utilizado para generar esta interfaz lo podrán encontrar como un proyecto de Netbeans en nuestro repositorio de Github.

El algoritmo cuenta con varias clases que cumplen con distintas funciones. A continuación describiré de manera general las partes principales de la aplicación:

• • El listado de ciudades con sus coordenadas: Para representar las ciudades y las coordenadas «x» y «y» de cada una decidí crear la clase «City», la cual permite construir objetos que almacenan los datos requeridos. Luego se crea una lista de ciudades, la cual será usada para realizar todos los cálculos. La lista de ciudades luce así:

Estas coordenadas las escogí de manera arbitraria, tratando de que hubiese cierta separación entre un punto y otro.

• • Cálculo de permutaciones: para calcular todas las rutas posibles entre ciudades diseñé una clase que me permite generar una lista con todas las posibles permitaciones con las etiquetas de las ciudades, en formato String.

Una permutación es una disposición de elementos de un conjunto en un orden específico. Por ejemplo, dado un conjunto de letras ABC, una permutación podría ser ABC, ACB, BAC, BCA, CAB, CBA. Cada una de estas permutaciones representa un orden diferente de las letras.

Basado en la lista de ciudades, el algoritmo genera permitaciones que no incluyen a la ciudad de partida. Por ejemplo, si el punto de partida es «A», el algoritmo genera las permitaciones BC y CB. Luego se agrega la ciudad de origen al inicio y al final de la cadena de caracteres. Esto da como resultado ACBA y ABCA. De esta forma nos aseguramos que algoritmo siempre parte de un punto en específico y regresa al mismo punto.

• • Cálculo de rutas: a partir de las permutaciones se calculan las rutas, separando las letras de las permutaciones en pares. Por ejemplo, si tenemos la permitación ABCD, el algoritmo generará las rutas AB, BC y CD. Utilizando las coordenadas de las dos ciudades que forman la ruta se calcula la distancia entre ellas, utilizando la distancia Euclidiana. El modelo sería el siguiente:

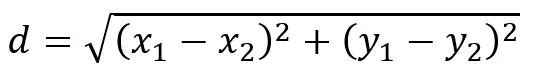
Cada ruta y su respectiva distancia se almacenan en una lista de objetos de la clase «Route».

• • Cálculo de tryectorias: Luego de calcular todas las rutas posibles y las distancias se procede a calcular las trayectorias, las cuales una combinación de rutas. Supongamos que el algoritmo genera la permutación ABCDA como una posible trayectoria. Para el cálculo de la distancia total de la trayectoria se procede a sumar la distancia entre AB, BC, CD y DA. De esta forma podemos conocer cual es la trayectoria que permite recorrer todas las ciudades en la menor distancia posible.

La representación gráfica se las ciudades y trayectorias se dibujan en un JPanel, para lo cual se ha creado la clase Canvas. Para el renderizado de la interfaz gráfica se ha utilizado distintos recursos, tales como ExecutorServices para el procesamiento en paralelo de los datos y la actualización en tiempo real del proceso de cálculo de rutas.

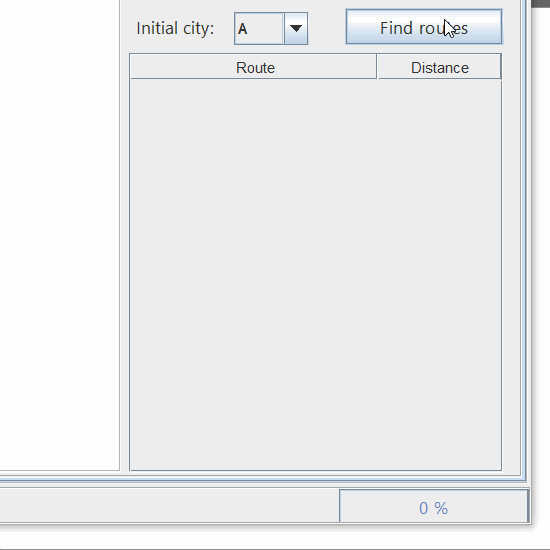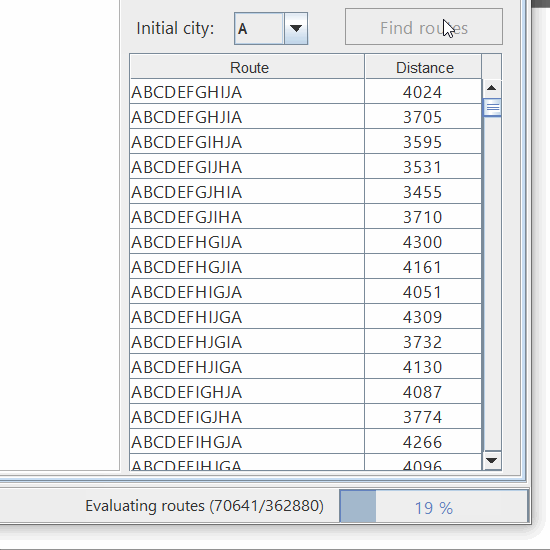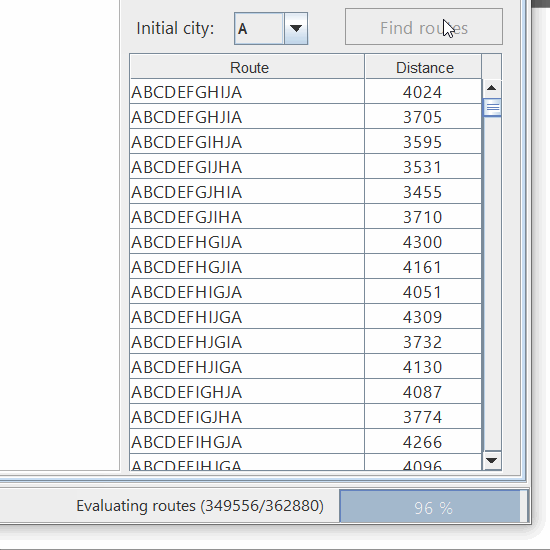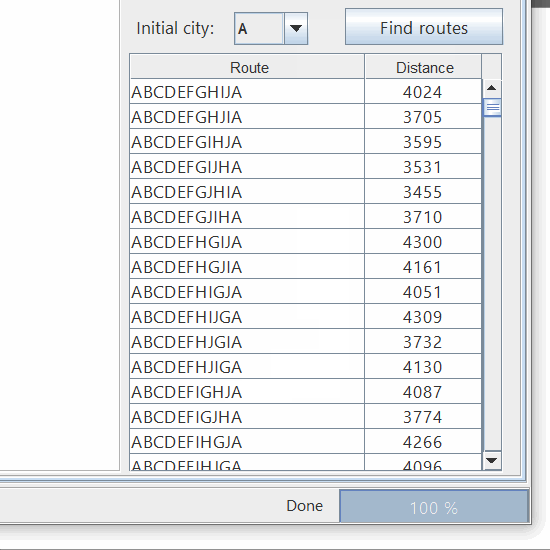Luego de calcular todas las rutas, el software permite ordenarlas y revisarlas una por una. De esta forma podemos ver cuales son las mejores y las peores rutas:

El software nos permite explorar las distintas permutaciones que se generan. Esto resulta extremadamente útil a la hora de hacer pruebas con algoritmos de optimización, pues nos permite evaluar si la respuesta de nuestro algoritmo es la óptima o si se encuentra entre las mejores posibles respuestas.

Esta aplicación también permite evaluar el tiempo de procesamiento, el cual dependerá de la cantidad de ciudades y del punto de partida que se utilice.

Como ya mencioné más arriba, este código y todo lo necesario para replicar estos resultados lo podrán encontrar como un proyecto de Netbeans en nuestro reporitorio de Github. Para correr la aplicación tendrán que ejecutar la clase TravelingSalesman.java en cuyo constructor se invoca el JFrame con la interfaz gráfica.

Conclusión

En este post se ha presentado una aplicación en Java para simular el problema del viajante (TSP) utilizando algoritmos de permutaciones, cálculo de distancias y una interfaz gráfica de usuario (GUI) para visualizar los resultados. Se ha dado una comprensión detallada del proceso de simulación y una guía paso a paso para aquellos interesados en implementar su propia solución del TSP en Java.

Es importante destacar que el problema del viajante es un problema NP-Hard, lo que significa que el tiempo de ejecución para resolverlo aumenta de forma exponencial con respecto al número de ciudades involucradas. Sin embargo, existen métodos heurísticos y métodos aproximados para encontrar soluciones óptimas. De estos métodos estaremos hablando en aportes futuros en este blog.

Espero que esta información haya sido de utilidad para ustedes. Cualquier duda o comentario me lo pueden hacer llegar a través de la sección de comentarios, ubicada más abajo en esta página.