En este post, exploraremos una de las técnicas de Machine Learning más interesantes y versátiles: el Modelo Oculto de Markov (HMM, por sus siglas en inglés). Este algoritmo es ampliamente utilizado en una variedad de aplicaciones, como la clasificación de secuencias, la detección de patrones y la predicción de eventos futuros.
En este post empezaremos con una introducción sobre lo que es un HMM y su aplicación en Machine Learning. Luego, construiremos un script en Python para generar un dataset de pruebas que será utilizado para entrenar un algoritmo HMM. Una vez que hayamos encontrado los parámetros adecuados para el algoritmo, lo probaremos en nuestro dataset para ver cómo funciona. Al final, podrás tener una comprensión más clara de cómo utilizar un HMM en Python.
Sin más que decir, empecemos.
¿Qué es el Modelo Oculto de Markov?
El Modelo Oculto de Markov (HMM, por sus siglas en inglés) es un modelo probabilístico que se utiliza para describir sistemas dinámicos que evolucionan en el tiempo y que son observables solo en parte. El HMM es una combinación de un modelo de Markov y un modelo de procesos estocásticos, y se utiliza para describir sistemas en los que no se conocen completamente los estados subyacentes, pero se tienen observaciones que están relacionadas con ellos.
Un modelo de Markov es un tipo de modelo estadístico que se utiliza para describir un proceso en el que el futuro estado depende solo del estado actual, y no de los estados previos. En otras palabras, en un modelo de Markov, la probabilidad de transición de un estado a otro solo depende del estado actual, y no de los estados previos. Esto se conoce como la propiedad de Markov, y permite que los modelos de Markov sean útiles para describir una amplia variedad de procesos, incluyendo la dinámica de sistemas financieros, la evolución de enfermedades, y la transmisión de información en redes.
En un HMM, cada estado subyacente es un proceso estocástico con una distribución de probabilidad que describe la probabilidad de observar una determinada observación en un momento dado. Además, el HMM también describe la probabilidad de transición de un estado a otro a lo largo del tiempo.
Un ejemplo de uso de un modelo oculto de Markov es en el reconocimiento de patrones en series de tiempo. Por ejemplo, supongamos que tienes datos sobre el clima en una ciudad durante un período de tiempo determinado. Desconoces la causa detrás de los patrones de clima, por lo que utilizas un modelo oculto de Markov para identificar patrones y predecir el clima futuro.
En este caso, el estado oculto sería la causa subyacente detrás de los patrones climáticos y las observaciones serían los datos climáticos. A través del aprendizaje automático, el Modelo Oculto de Markov aprenderá la probabilidad de transición entre diferentes estados ocultos y la distribución de probabilidad de las observaciones asociadas a cada estado oculto. Finalmente, el modelo puede utilizarse para hacer predicciones sobre el clima futuro.
¿Para qué se utiliza?
Algunos ejemplos de aplicaciones de los modelos HMM incluyen:
- Reconocimiento de voz y lenguaje: El HMM se utiliza en el reconocimiento de voz y lenguaje para identificar patrones en la secuencia de sonidos o palabras habladas.
- Análisis de secuencias de ADN y proteínas: En el análisis de secuencias de ADN y proteínas se utiliza para identificar patrones en la secuencia de nucleótidos o aminoácidos.
- Análisis financiero: predicciones del comportamiento futuro del mercado financiero o para identificar patrones en los precios de las acciones.
- Detección de fallos en sistemas: se utiliza para identificar patrones en los datos de los sensores del sistema y predecir posibles fallos antes de que ocurran.
- Modelado de tráfico en redes de comunicaciones: En el modelado de tráfico en redes de comunicaciones, el modelo oculto de Markov se utiliza para predecir el tráfico de datos en una red y optimizar su uso para garantizar la eficiencia y la calidad del servicio.
- Análisis de señales: los modelos HMM pueden utilizarse para identificar patrones en señales de audio, video o sensores.
- Sistemas de recomendación: se utilizan para recomendar productos o servicios a usuarios basados en sus acciones previas y preferencias.
- Procesamiento de imágenes: identificación de objetos en imágenes y analizar su movimiento.
- Predicción de series temporales: predicción del comportamiento futuro de una serie temporal, como el precio de una acción o la temperatura en una ciudad.
- Sistemas de control de tráfico: pueden utilizarse para monitorear y controlar el tráfico en una red, optimizando el uso de recursos y minimizando los tiempos de espera.
Ejemplo de uso
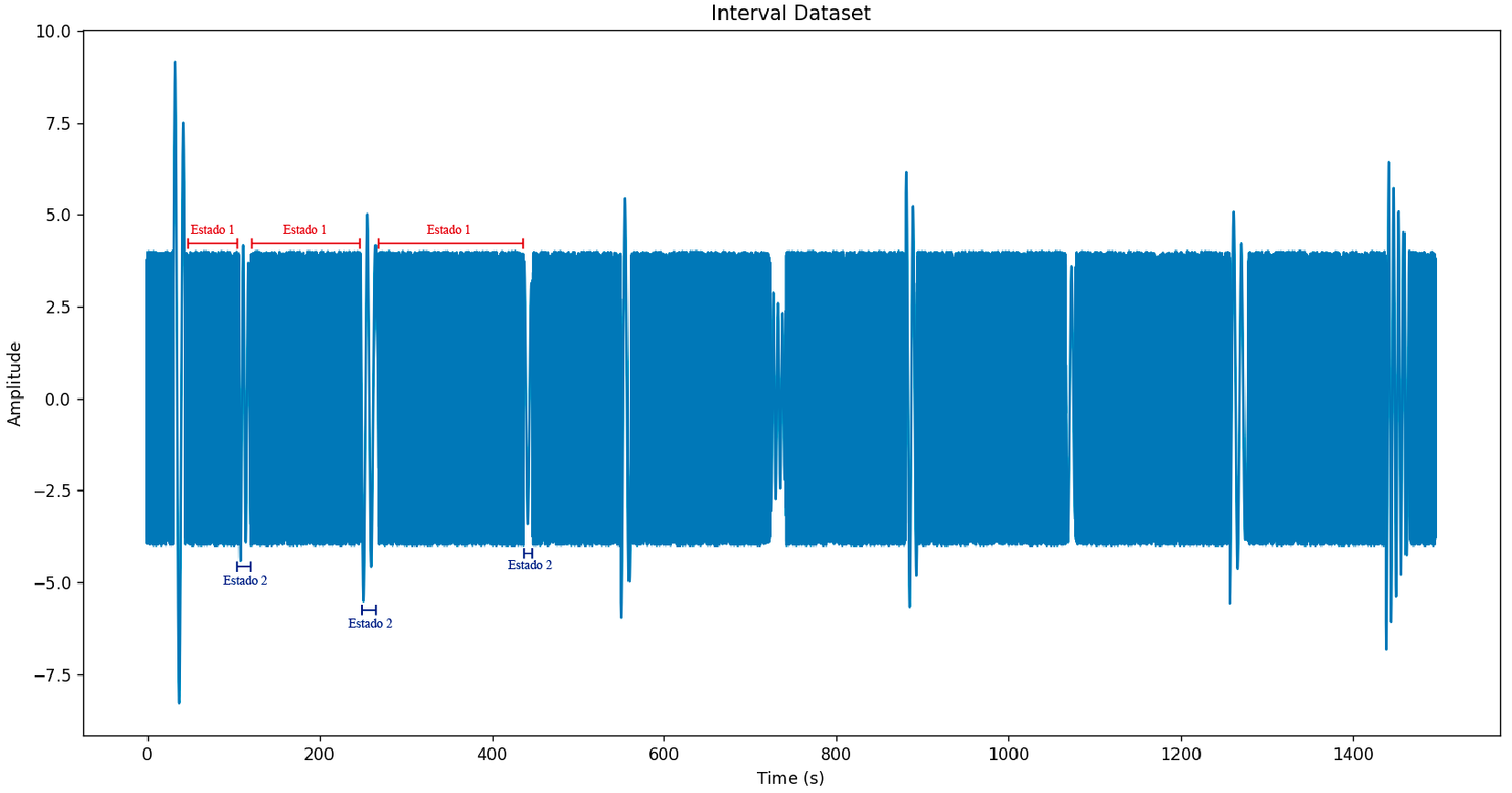
Para demostrar la utilidad de este algoritmo voy a construir un dataset de pruebas que nos permita ilustrar el uso y la utilidad de HMM. El dataset luce así:
Se trata de un conjunto de números aleatorios entre 4 y -4. En medio de ese conjunto de datos hay 10 intérvalos de duración aleatoria y separados por intervalos de tiempo aleatorios. En estos intervalos se insertan oscilaciones en la forma de ondas senoidales amortiguadas, con frecuencia y amplitud aleatorias.
Para la creación de este dataset construi un algoritmo en Python, en el cual se pueden configurar distintos parámetros para definir las características que tendrá el conjunto de datos. El script lo podrán encontrar en nuestro repositorio de Github.
Ahora que tenemos el dataset de pruebas trataremos de «aislar» las oscilaciones. Vamos a eliminar todo el ruido del dataset y nos quedaremos con las oscilaciones.
Para esto utilizaremos el HMM para aislar los posibles estados en el dataset. Consideraremos que hay dos estados, el estado sin oscilaciones y el estado con oscilaciones.
El HMM nos ayudará a separar los datos en estados. Para hacer esto, utilizaremos el siguiente código:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 |
import numpy as np import pandas as pd import matplotlib.pyplot as plt from hmmlearn import hmm import joblib # Load the data from the CSV file into a pandas DataFrame df = pd.read_csv("dataset.csv", header=None, names=["Time", "Value"]) # Extract the "Value" column as the observations for the HMM observations = df["Value"].values.reshape(-1, 1) # Define the number of states for the HMM n_states = 2 # Initialize the HMM model model = hmm.GaussianHMM(n_components=n_states, covariance_type="full") # Fit the HMM model to the observations model.fit(observations) # Predict the hidden states for each observation hidden_states = model.predict(observations) # Filter the hidden states filtered_hidden_states = np.full_like(hidden_states, -1) # Create an array of the same shape as hidden_states with all elements set to -1 current_state = hidden_states[0] # Set the initial state to the first element of hidden_states cluster_length = 1 # Initialize the length of the current cluster to 1 # Loop through all elements in hidden_states for i in range(1, len(hidden_states)): if hidden_states[i] == current_state: # If the current state is still the same as the previous state cluster_length += 1 # Increase the length of the current cluster by 1 else: if cluster_length >= 75: # If the length of the current cluster is greater than or equal to 75 filtered_hidden_states[i-cluster_length:i] = 3 # Assign the value of 3 to the corresponding range of filtered_hidden_states current_state = hidden_states[i] # Set the current state to the current element of hidden_states cluster_length = 1 # Reset the length of the current cluster to 1 # Print the filtered hidden states print("Filtered Hidden States:", filtered_hidden_states) print("Number of States:", model.n_components) # Save the model filename = 'trained_model.joblib' joblib.dump(model, filename) # Load the saved model loaded_model = joblib.load(filename) # Plot the observations and filtered hidden states fig, ax = plt.subplots() ax.plot(observations, label="Observations") ax.plot(filtered_hidden_states, label="Filtered Hidden States") ax.legend() ax.set_xlabel("Time") ax.set_ylabel("Value") plt.show() |
Este código aplicará el HMM para buscar los dos estados ocultos (n_states = 2). Luego aplicará un postprocesamiento en el que se eliminarán los clusters de menos de 75 muestras.
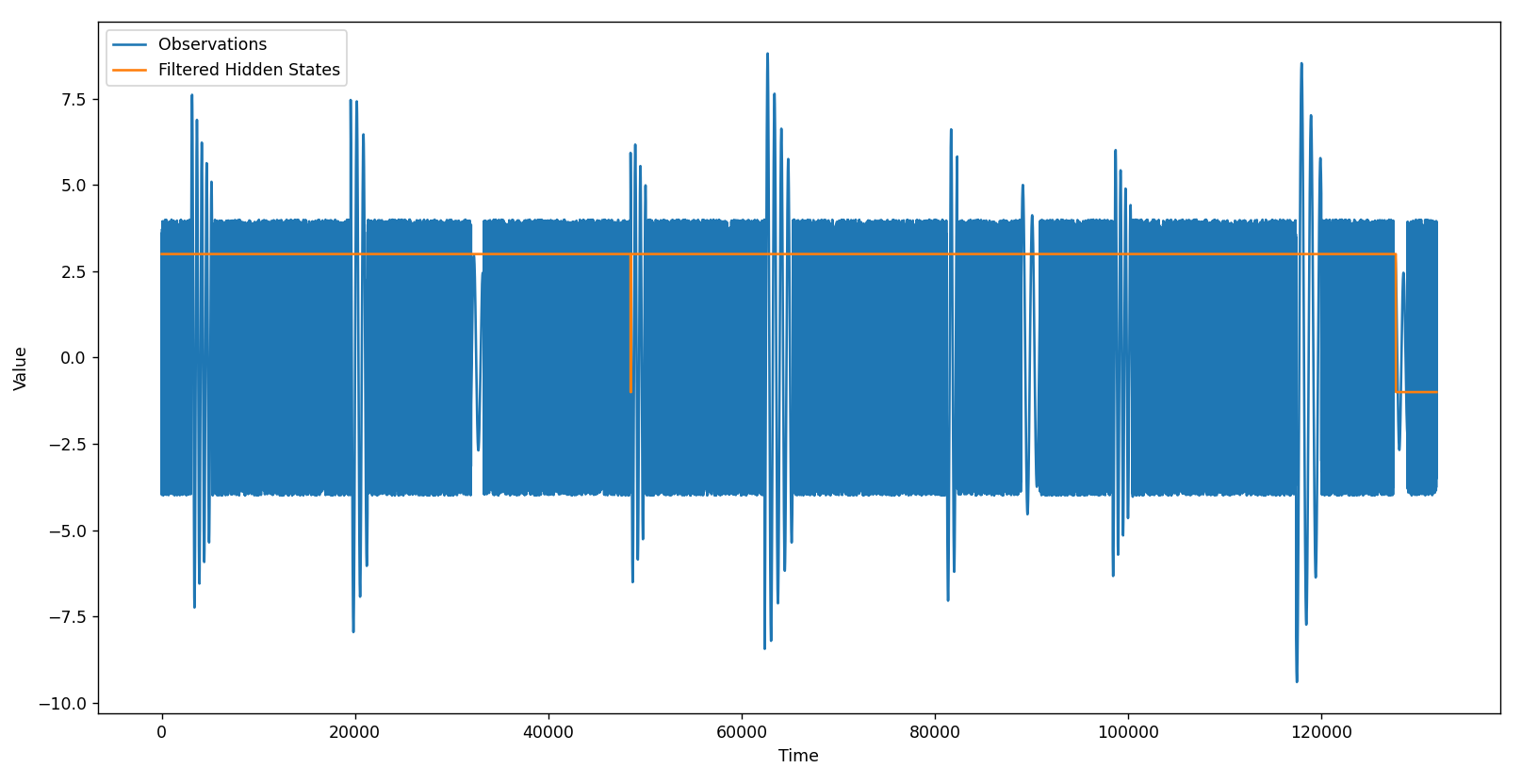
La razón para esto es muy simple. El resultado de aplicar el algoritmo HMM, visualmente, es el siguiente:
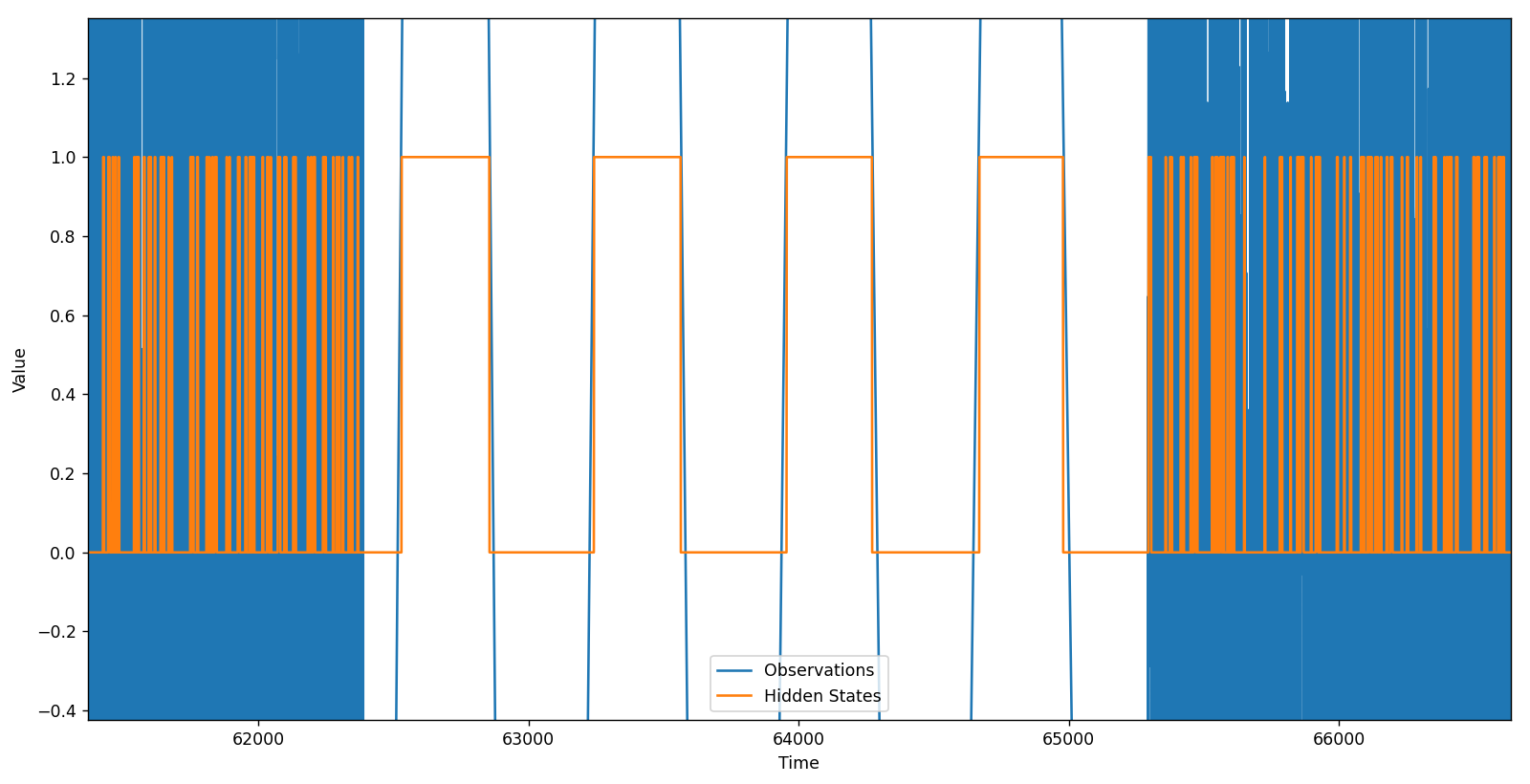
Los datos en color naranja son el resultado de la clasificación de cada dato en uno de los dos estados definidos. Visto de esta forma no parece ser muy útil, pero si hacemos zoom en alguno de los steps veremos algo interesante:
Vemos que durante los intérvalos con oscilaciones la salida del HMM se decanta entre los dos posibles estados. En el resto de los datos los estados oscilan de manera prácticamente aleatoria. Aprovechando la estabilidad de los estados durante las oscilaciones podemos filtrar los estados de salida, de manera tal que si un estado se mantiene por menos de 75 muestreos, se considere el estado como «-1». De lo contrario, se le considere «3». Estos valores los he escogido de manera arbitraria y no por alguna razón en particular.
Luego del filtrado, el resultado luce así:
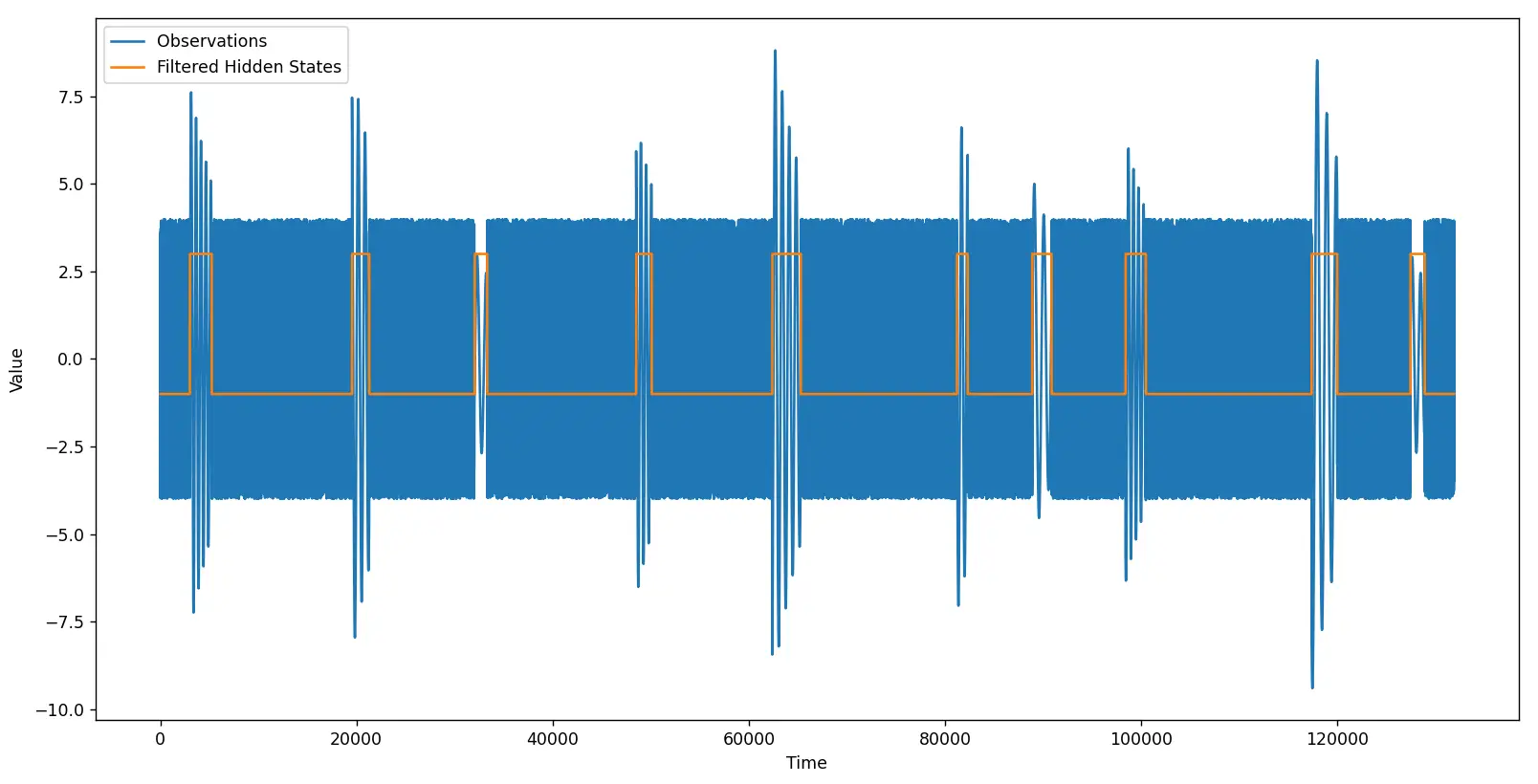Vemos que la línea naranja logra resaltar correctamente todos y cada uno de las oscilaciones. Sin embargo, el Modelo Oculto de Markov es un algoritmo probabilístico que produce resultados aleatorios en cada ejecución. Por esta razón es posible que cuando ejecutemos el script el resultado obtenido no sea el esperado.
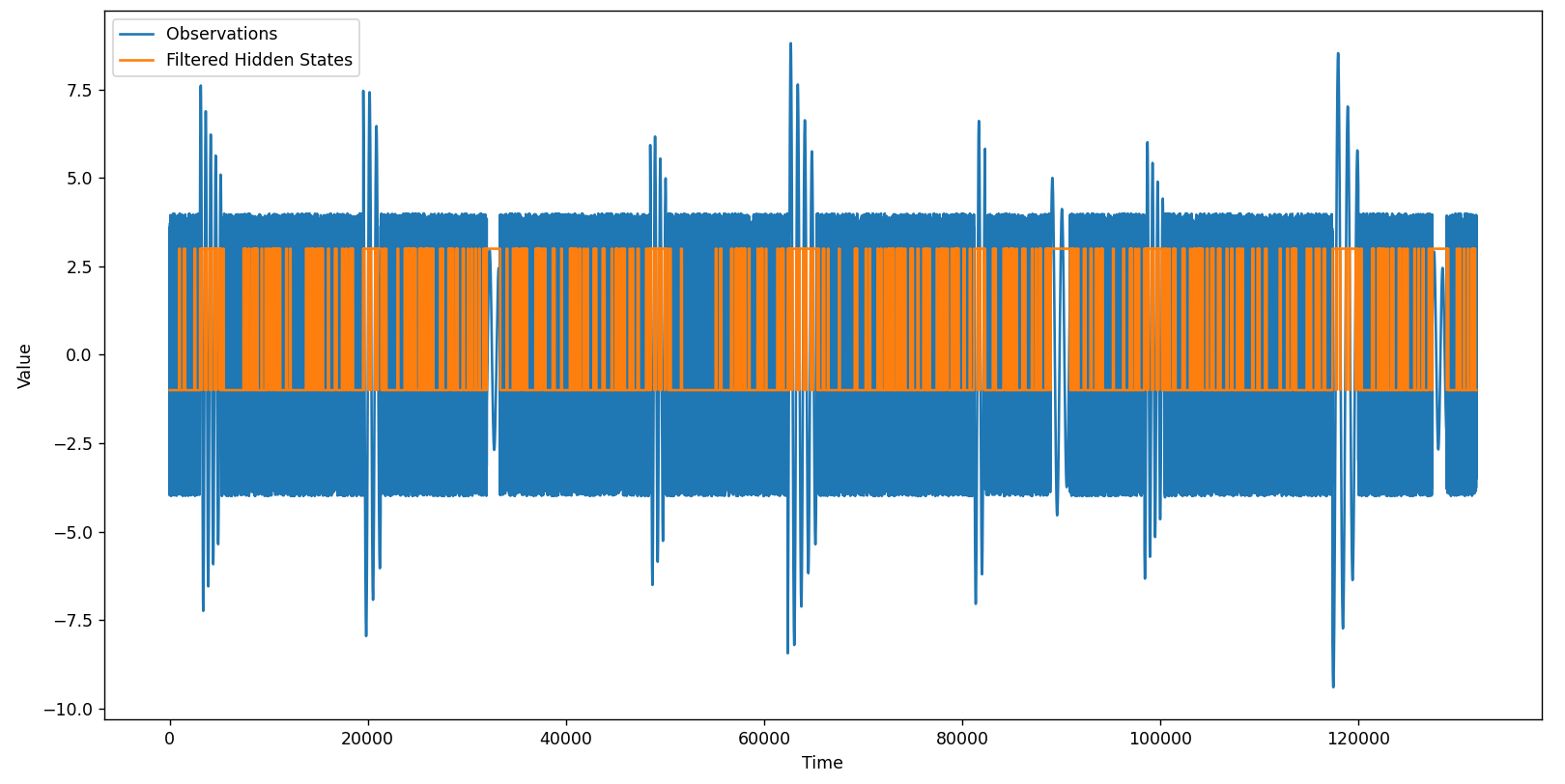
Luego de varias ejecuciones se logra que el algoritmo identifique los estados deseados. Es importante que cuando encontremos un resultado correcto salvemos el «entrenamiento» del modelo en un archivo «trained_model.joblib». Luego, con el siguiente script, podemos utilizar el archivo entrenado para clasificar datos:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
import numpy as np import pandas as pd import matplotlib.pyplot as plt import joblib # Load the saved model filename = 'trained_model.joblib' loaded_model = joblib.load(filename) # Load the data from the CSV file into a pandas DataFrame df = pd.read_csv("dataset.csv", header=None, names=["Time", "Value"]) # Extract the "Value" column as the observations for the HMM observations = df["Value"].values.reshape(-1, 1) # Predict the hidden states for each observation using the loaded model hidden_states = loaded_model.predict(observations) # Filter the hidden states filtered_hidden_states = np.full_like(hidden_states, 0) current_state = hidden_states[0] cluster_length = 1 for i in range(1, len(hidden_states)): if hidden_states[i] == current_state: cluster_length += 1 else: if cluster_length >= 75: filtered_hidden_states[i-cluster_length:i] = 3 current_state = hidden_states[i] cluster_length = 1 for i in range(0, len(filtered_hidden_states)): if (filtered_hidden_states[i]==0): observations[i]=0 # Print the filtered hidden states print("Filtered Hidden States:", filtered_hidden_states) # Plot the observations and filtered hidden states fig, ax = plt.subplots() ax.plot(observations, label="Observations") ax.plot(filtered_hidden_states, label="Filtered Hidden States") ax.legend() ax.set_xlabel("Time") ax.set_ylabel("Value") plt.show() |
Este código logrará replicar los resultados correcto cada vez que se ejecute. Ambos scripts, el de entrenamiento y el que utiliza el archivo entrenado, se encuentran disponibles en nuestro repositorio de Github.
Con este último script, el resultado es el siguiente:
Bastante bien, debo decir. Luego de aislar las oscilaciones del resto de datos podemos utilizar esta información para entrenar algún modelo de Machine Learning supervisado que nos permita detectar oscilaciones similares a las mostradas en este post.
Este es apenas un pequeño vistazo al potencial del algoritmo HMM para proyectos de Data Science y Machine Learning en general.
Comentarios finales
En resumen, el Modelo Oculto de Markov (HMM) es una técnica de Machine Learning versátil y ampliamente utilizada en una variedad de aplicaciones, como la clasificación de secuencias, la detección de patrones y la predicción de eventos futuros. Es un modelo probabilístico que combina un modelo de Markov y un modelo de procesos estocásticos para describir sistemas dinámicos observables solo en parte.
El ejemplo presentado en este post es el uso del Modelo Oculto de Markov en el análisis de patrones en una serie temporal. Se menciona cómo el HMM es ampliamente utilizado en una variedad de aplicaciones, incluyendo la detección de patrones y la predicción de eventos futuros. En este caso en particular, se espera utilizar el algoritmo para construir un dataset de entrenamiento supervisado para un contador de pasos a partir de las mediciones de un acelerómetro y un giroscopio.
La idea es utilizar HMM para aislar las oscilaciones del ruido del acelerómetro con un enfoque similar al mostrado en el post. En resumen, el post introduce la versatilidad y utilidad del Modelo Oculto de Markov en el análisis de patrones y su aplicación a diferentes problemas.
Esperamos que hayas encontrado esta introducción interesante y útil. Si tienes alguna pregunta o comentario, no dudes en compartirlo con nosotros. ¡Gracias por leer!
