Desde que comencé a escribir artículos sobre Machine Learning aquí en Panama Hitek, me he propuesto explorar una amplia variedad de temas interesantes relacionados con esta disciplina, yendo más allá del simple uso de los algoritmos disponibles en la actualidad. En muchos de los artículos que he compartido hasta ahora, me he centrado en desarrollar algoritmos que implementen métodos de clasificación y probarlos en el conjunto de datos MNIST.
Sin embargo, hay algo que ha captado mi atención: todos los casos que hemos abordado hasta ahora utilizan la misma representación de datos del conjunto de datos MNIST, que consiste en un array unidimensional de 784 columnas. En el campo del Machine Learning, esto se conoce como un «flattened input array».
Para explicar este concepto de una manera más clara, les he preparado esta imagen:
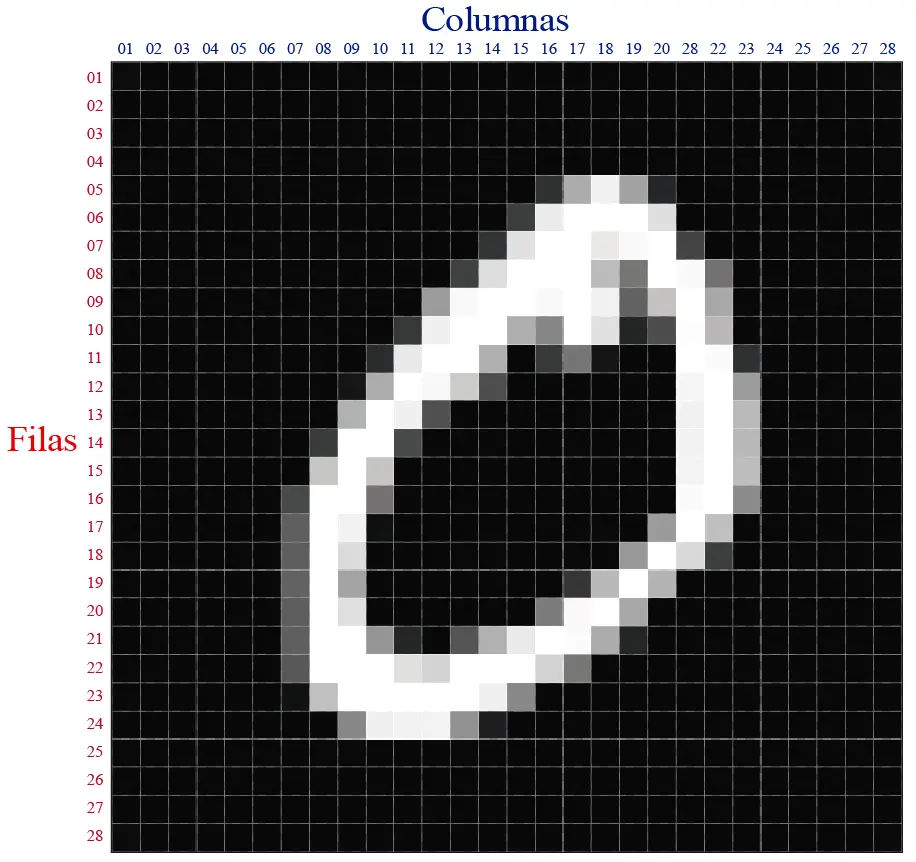
La imagen muestra uno de las imágenes del dataset MNIST. Todas las muestras de este dataset son imágenes de dígitos con una resolución de 28×28. En total, la imagen cuenta con 784 pixeles (28 x 28 = 784), donde cada pixel es representado por un valor entre 0 y 255. Un pixel representado por 0 es un pixel negro, mientras que un pixel de 255 es un pixel completamente blanco. Un pixel gris se puede representar con un número proporcional al valor de la intensidad del color.
La mayoría de los algoritmos que hemos probado aquí (Random Forests, KNN, Redes Neuronales, Support Vector Machine, etc) utilizan una representación «aplanada» (flatenned) de estas imágenes, donde cada fila de pixeles se juntan una al lado de la otra para formar una única fila de 784 pixeles.
Aquí les dejo una representación gráfica del proceso de convertir una imagen de 2 dimensiones en una imagen de una sola dimensión, el «flatenning».
Cada fila es separada en una única fila de 28 pixeles. Luego cada fila es puesta una al lado de la otra para convertirse en una única fila formada por las 28 filas originales. Por supuesto que en contexto de Machine Learning este procedimiento no se hace de esta manera. Esta animación es simplemente una representación gráfica para que se entienda el concepto.
En el post sobre PyTorch y MNIST: Cómo entrenar una red neuronal para clasificación de imágenes presenté la siguiente imagen:
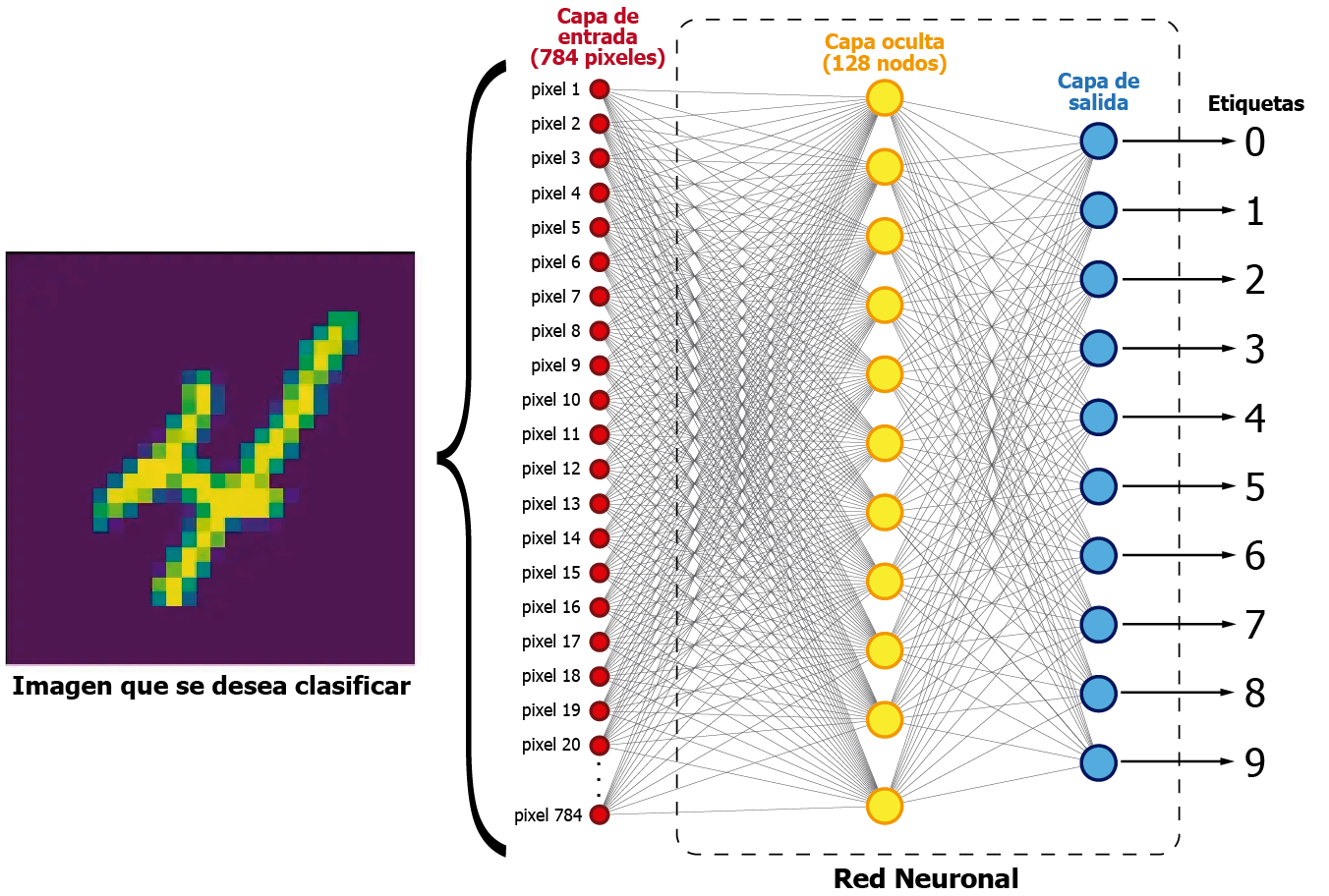
Aquí podemos observar una representación gráfica de una red neuronal utilizada para clasificación de imágenes. Esta red cuenta con 784 nodos de entrada, los cuales representan los valores de los pixeles de la imagen. Esta red permite clasificar las imágenes en los números que representan, con un 97.81% de eficacia.
Dicho esto, me intriga la posibilidad de introducir los datos de entrada a la red neuronal en un formato bidimensional en lugar de unidimensional. En lugar de utilizar una matriz de una fila y 784 columnas, propongo emplear una matriz de 28 filas por 28 columnas, similar a las imágenes previamente mostradas.
Esta propuesta tiene sentido, ¿no crees? Para los seres humanos resulta más natural reconocer una imagen en formato 2D que cuando se encuentra representada como una única fila de píxeles. Existen patrones en las imágenes que pueden ser fácilmente identificables en dos dimensiones, pero que podrían pasar desapercibidos en una dimensión.
Motivado por esta idea, me propuse tratar de descubrir cuáles son las técnicas utilizadas para emplear datos multidimensionales como entrada en algoritmos de aprendizaje automático (Machine Learning). Descubrí que la mayoría de los algoritmos clásicos de Machine Learning utilizan datos de entrada unidimensionales. Aún así, existen opciones para procesar datos de entrada multidimensionales, específicamente utilizando redes neuronales convolucionales.
Redes Neuronales Convolucionales
Las redes neuronales convolucionales (CNN por sus siglas en inglés, Convolutional Neural Networks) son un tipo de arquitectura de redes neuronales diseñadas para procesar datos en formato multidimensionales, como imágenes. Estas redes han demostrado ser muy efectivas en tareas de visión por computadora, reconocimiento de imágenes y procesamiento de datos espaciales.
La principal característica de las CNN es su capacidad para aprender y extraer automáticamente características relevantes de las imágenes a través de capas convolucionales. Estas capas convolucionales aplican filtros o kernels a las regiones de la imagen, lo que permite detectar patrones locales, como bordes, texturas o formas específicas. Estas características se capturan y combinan en capas subsiguientes mediante operaciones como el submuestreo o el agrupamiento (pooling), lo que reduce la dimensionalidad de los datos y conserva las características más relevantes.
Además de las capas convolucionales, las CNN también suelen incluir capas de activación no lineales, como la función ReLU (Rectified Linear Unit), que introducen la no linealidad en el modelo y ayudan a capturar relaciones más complejas entre las características. También pueden incluir capas de normalización, como la normalización por lotes (batch normalization), que estandarizan los valores de las características y aceleran el entrenamiento de la red.
Al final de la arquitectura de una CNN, se suelen utilizar capas totalmente conectadas (fully connected layers) para realizar la clasificación o la predicción final. Estas capas toman las características extraídas por las capas convolucionales y las utilizan para generar una salida final.
La siguiente imagen muestra una representación muy básica de una red neuronal convolucional:
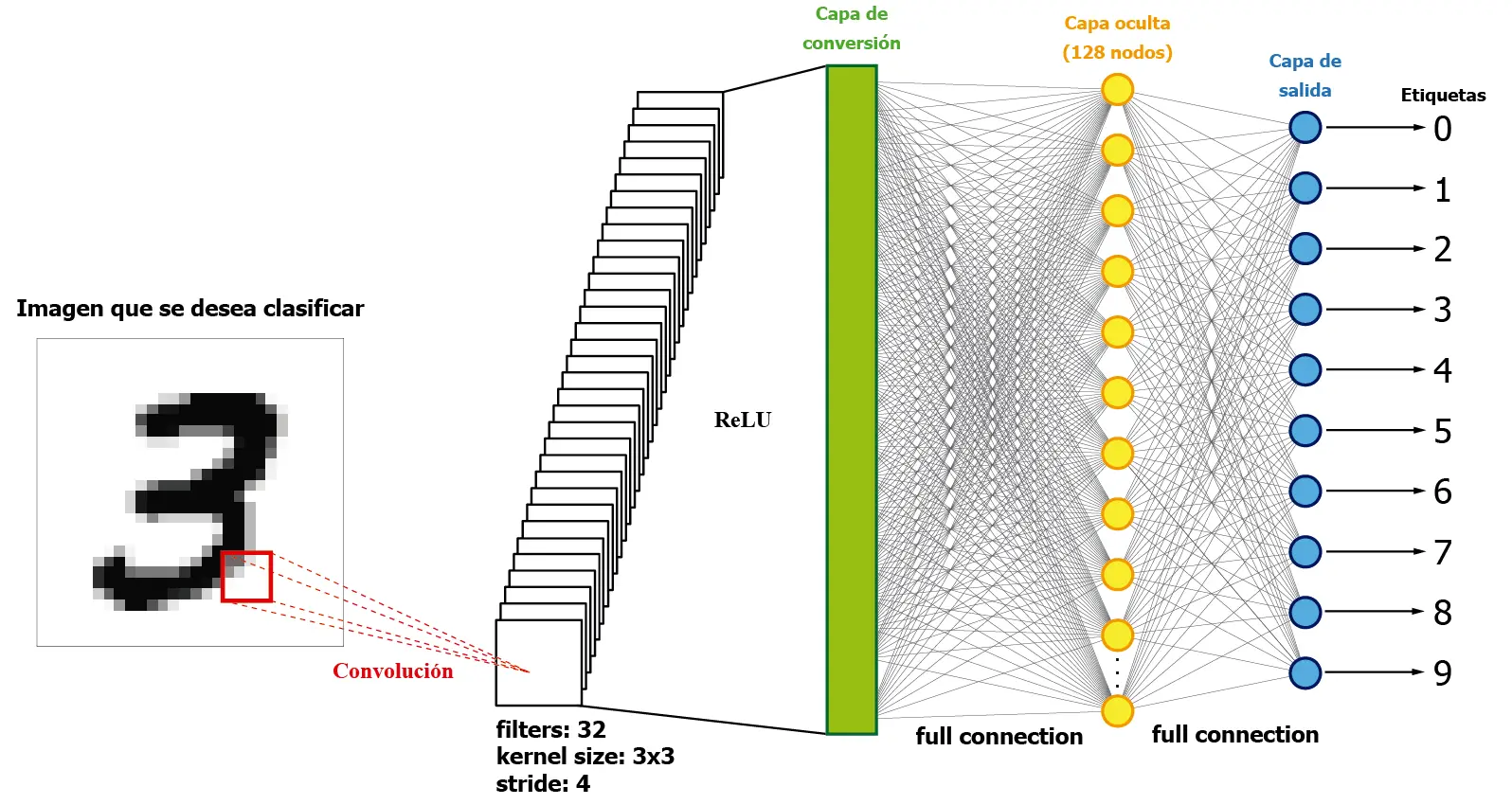
La imagen presentada muestra una simplificación de la estructura de una red neuronal convolucional. La red se compone de una imagen de entrada en forma de datos 2D. Esta imagen se introduce en la red a través de una capa convolucional, que realiza operaciones de convolución al multiplicar matricialmente pequeñas partes de la imagen por los filtros de la capa convolucional. Como resultado, se obtiene una estructura multidimensional de datos, que puede convertirse en una estructura unidimensional utilizando un Lineal Layer (representado en la imagen como «Capa de conversión»).
Después de la conversión de los datos de entrada de una estructura multidimensional a una dimensión, la red neuronal utiliza la estructura tradicional de capas ocultas completamente interconectadas para mapear los resultados de la clasificación en la capa de salida, que consta de 10 nodos en este caso.
Codificación de la red neuronal convolucional
El código que describe la red condolucional mostrada en la imagen anterior lo podrán encontrar en nuestro repositorio de Github. Se trata de una red neuronal codificada en Pytorch, con una capa convolucional en la entrada, una capa de conversión a 128 nodos y 10 nodos de salida. Similar a la de nuestro post de redes neuronales simples con Pytorch.
Este es el código de la red neuronal convoluciona:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 |
# Import necessary libraries import pandas as pd import numpy as np import time as time import torch import torch.nn as nn import torch.optim as optim from torch.utils.data import DataLoader, TensorDataset # Define the number of training and testing samples trainingSamples = 50000 testingSamples = 10000 """ Set global variables for the computing time of both training and testing """ startTrainingTime = 0 endTrainingTime = 0 trainingTime = 0 startTestingTime = 0 endTestingTime = 0 testingTime = 0 # Function for loading data from a CSV file and returning the data and labels def loadDataset(fileName, samples): x = [] # Array for data inputs y = [] # Array for labels (expected outputs) # Load data from a CSV file and store it in a pandas DataFrame object with open(fileName, 'r') as f: train_data = pd.read_csv(f) # Extract labels from the first column of the DataFrame object y = np.array(train_data.iloc[0:samples, 0]) # Extract data from the remaining columns of the DataFrame object and normalize it x = np.array(train_data.iloc[0:samples, 1:]).reshape(-1, 28, 28) / 255 # Convert the data and labels to PyTorch tensors x = torch.tensor(x, dtype=torch.float32) y = torch.tensor(y, dtype=torch.long) # Return the data and labels return x, y # Define a simple neural network class class ConvolutionalNeuralNetwork(nn.Module): def __init__(self): super(ConvolutionalNeuralNetwork, self).__init__() # Define a convolutional layer with 1 input channel, 32 output channels, and a kernel size of 3x3 self.conv1 = nn.Conv2d(1, 32, kernel_size=3) # Define a fully connected layer with 32*26*26 input features and 128 output features self.fc1 = nn.Linear(32 * 26 * 26, 128) # Define a fully connected layer with 128 input features and 10 output features (for the 10 digits) self.fc2 = nn.Linear(128, 10) # Define the activation function as ReLU self.activation = nn.ReLU() def forward(self, x): # Pass the input through the convolutional layer and apply the activation function x = self.conv1(x) x = self.activation(x) # Flatten the output of the convolutional layer x = x.view(-1, 32 * 26 * 26) # Pass the flattened output through the first fully connected layer and apply the activation function x = self.fc1(x) x = self.activation(x) # Pass the output of the first layer through the second fully connected layer x = self.fc2(x) # Return the output return x # Main function def main(): # Load the training and testing datasets train_x, train_y = loadDataset("../../../../datasets/mnist/mnist_train.csv", trainingSamples) test_x, test_y = loadDataset("../../../../datasets/mnist/mnist_test.csv", testingSamples) # Define the batch size for training and testing data batchSize = 64 # Define a DataLoader object for the training data train_loader = DataLoader(TensorDataset(train_x, train_y), batch_size=batchSize, shuffle=True) # Define a DataLoader object for the testing data test_loader = DataLoader(TensorDataset(test_x, test_y), batch_size=batchSize) device = torch.device("cuda" if torch.cuda.is_available() else "cpu") # Use GPU if available, otherwise use CPU # Create a SimpleNeuralNetwork object and define the loss function and optimizer model = ConvolutionalNeuralNetwork().to(device) loss_function = nn.CrossEntropyLoss() optimizer = optim.Adam(model.parameters()) # Train the model and measure the time startTrainingTime = time.time() # Set the number of epochs for training epochs = 20 # Loop over the specified number of epochs for epoch in range(epochs): epoch_loss = 0.0 epoch_accuracy = 0.0 # Loop over the batches of training data for i, data in enumerate(train_loader): inputs, labels = data inputs = inputs.unsqueeze(1).to(device) # Add a channel dimension and move to the same device as the model labels = labels.to(device) # Move labels to the same device as the model # Zero the gradients of the model parameters optimizer.zero_grad() # Forward pass through the model outputs = model(inputs) # Calculate the loss loss = loss_function(outputs, labels) # Backward pass through the model and update the parameters loss.backward() optimizer.step() # Update the epoch loss and accuracy epoch_loss += loss.item() _, predicted = torch.max(outputs.data, 1) correct = (predicted == labels).sum().item() epoch_accuracy += correct / batchSize # Print out the epoch loss and accuracy print("Epoch:", epoch + 1, " Loss:", epoch_loss / len(train_loader), " Accuracy:", epoch_accuracy / len(train_loader)) endTrainingTime = time.time() trainingTime = endTrainingTime - startTrainingTime # Evaluate the model on the testing data and measure the time validResults = 0 totalSamples = 0 startTestingTime = time.time() with torch.no_grad(): for i, data in enumerate(test_loader): inputs, labels = data inputs = inputs.unsqueeze(1).to(device) # Add a channel dimension and move to the same device as the model labels = labels.to(device) # Move labels to the same device as the model # Forward pass through the model outputs = model(inputs) _, predicted = torch.max(outputs.data, 1) results = predicted.tolist() expectedResults = labels.tolist() for result, expectedResult in zip(results, expectedResults): outcome = "Fail" if result == expectedResult: validResults += 1 outcome = " OK " totalSamples += 1 accuracy = (validResults / totalSamples) * 100 print( "Nº ", totalSamples, " | Expected result: ", expectedResult, " | Obtained result: ", result, " | ", outcome, " | Accuracy: ", round(accuracy, 2), "%") endTestingTime = time.time() testingTime = endTestingTime - startTestingTime # Calculate and print out the training and testing time and the testing accuracy print("-------------------------------") print("Results") print("-------------------------------") print("Training samples: ", trainingSamples) print("Training time: ", round(trainingTime, 2), " s") print("Testing samples: ", testingSamples) print("Testing time: ", round(testingTime, 2), " s") print("Testing accuracy: ", round((validResults / testingSamples) * 100, 2), "%") # Run the main function if this file is being executed directly if __name__ == "__main__": main() |
El resultado de ejecutar este código es el siguiente:
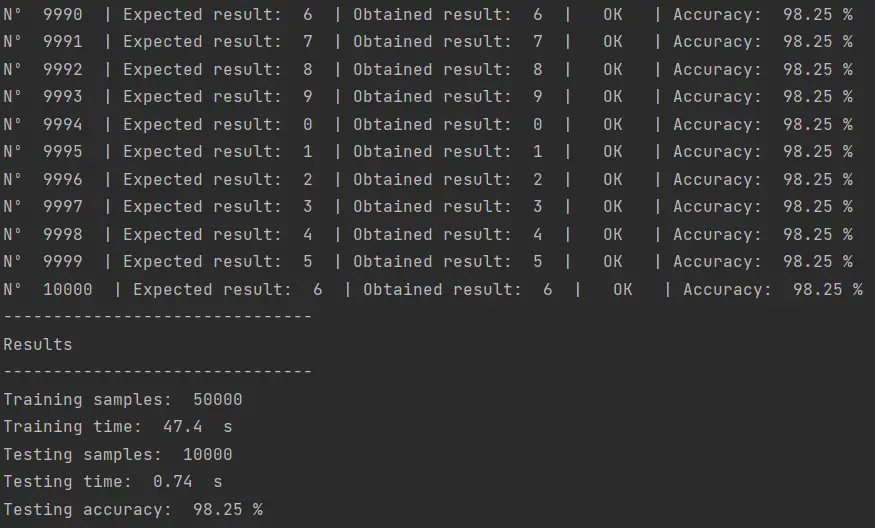
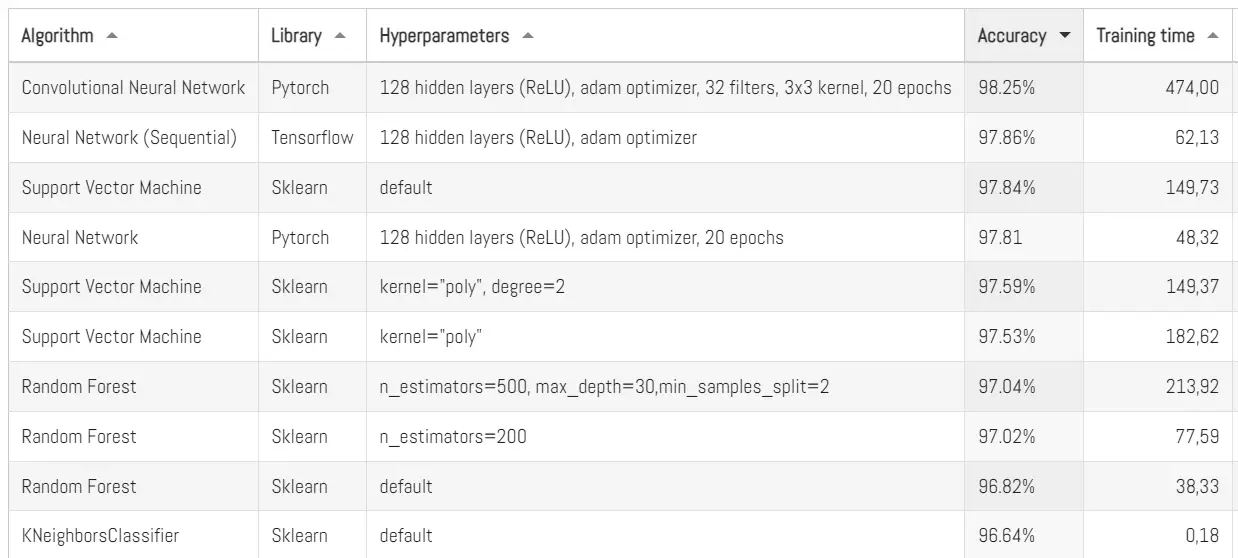
De todos los códigos que he probado hasta ahora en esta tarea de clasificación con MNIST, este algoritmo es el que ha alcanzado el mayor nivel de precisión. Esto a pesar de que se trata de una implementación muy básica que podría ser optimizada a través de una cuidadosa selección de hiperparámetros o agregando más capas a la extructura de la red neuronal. Pero de eso hablaremos después.
Aquí les dejo el top actualizado de los mejores algoritmos que hemos probado con MNIST:
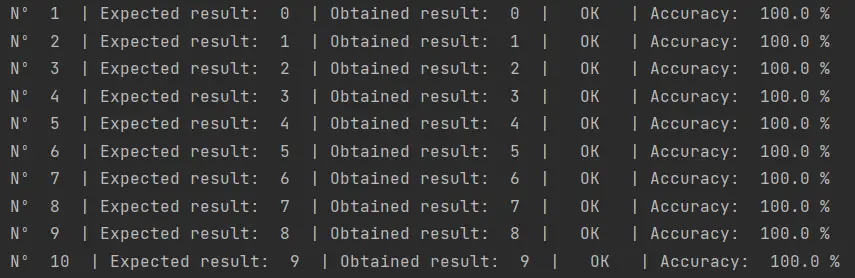
También lo probé con mis propios números manuscritos, algo que ya he hecho en otras ocasiones con otros algoritmos que hemos probado. La red neuronal convolucional, por primera vez, logró clasificar correctamente los 10 números que escribí a mano:
Les recuerdo que en mi post sobre Analizando mi escritura con Machine Learning en Python construí mi propio dataset de numeros manuscritos:
Hasta ahora ningún algoritmo había logrado clasificar correctamente los 10 números.
Conclusiones
En Machine Learning, la representación de datos desempeña un papel crucial en el rendimiento de los algoritmos. En el caso del conjunto de datos MNIST, se ha utilizado ampliamente la representación «aplanada» de las imágenes como un array unidimensional de 784 columnas en diferentes algoritmos de clasificación. Sin embargo, explorar nuevas formas de representar los datos puede llevar a resultados más precisos y una mejor comprensión de los patrones en las imágenes. Esto logramos demostrarlo en este post.
Se propuso utilizar una representación bidimensional de las imágenes, manteniendo su estructura original de filas y columnas. Para ello, las redes neuronales convolucionales (CNN) se presentan como una opción poderosa. Estas redes han demostrado su eficacia en tareas de visión por computadora y reconocimiento de imágenes al aprender y extraer automáticamente características relevantes a través de capas convolucionales.
En el contexto del conjunto de datos MNIST, podemos aprovechar la estructura bidimensional de las imágenes al introducir los datos de entrada en la red neuronal a través de una capa convolucional. Esta capa realiza operaciones de convolución, multiplicando matricialmente pequeñas partes de la imagen con filtros específicos. Esto permite capturar patrones locales y extraer características relevantes.
Es importante destacar que, después de esta etapa, es necesaria la conversión de la estructura multidimensional de datos a una estructura unidimensional mediante una capa de conversión o «Lineal Layer». Esto permite utilizar la estructura tradicional de capas ocultas completamente interconectadas en la red neuronal, las cuales clasifican las características extraídas en la capa de salida.
En resumen, al emplear redes neuronales convolucionales y aprovechar la estructura bidimensional de las imágenes en el conjunto de datos MNIST, se abre una nueva vía para mejorar la precisión de los algoritmos de clasificación y comprender mejor los patrones presentes en las imágenes. La exploración de nuevas representaciones y técnicas en Machine Learning es fundamental para avanzar en el campo y obtener resultados más precisos y confiables en diversas aplicaciones.
Espero que la información presentada en este post les haya sido útil. Cualquier duda o comentario me lo pueden hacer llegar a través de la sección de comentarios.
