Ley de los voltajes de Kirchhoff: Método de Mallas

En este post escribiré sobre la Ley de los voltajes de Kirchhoff, una de las principales leyes de la electricidad utilizadas en el análisis de circuitos eléctricos y electrónicos. Al uso de esta ley se le conoce como análisis de circuitos por mallas, lo cual forma parte de los cursos que incluyen análisis de circuitos eléctricos, tanto a nivel de escuela secundaria como en las universidades orientadas a la enseñanza de la ingenierí­a.

Cualquier persona que haya estudiado algún curso sobre análisis de circuitos eléctricos sabe que el análisis de circuitos por mallas y el análisis de circuitos por nodos son los dos principales métodos de análisis. Dependiendo del circuito también es posible hacer análisis de circuitos por el método de superposición, transformación de fuentes, análisi matricial o los teoremas de Thévenin y Norton. Sobre algunos de estos temas ya hemos hecho publicaciones en este blog:

• • Ley de corriente de Kirchhoff: Análisis de nodos
  • Leyes de Kirchhoff: El método Zbus

En esta ocasión lo que haremos será contabilizar los voltajes de cada elemento en una trayectoria cerrada e igualarlos a cero. De eso se trata el análisis de circuitos por mallas. Pero antes de entrar en materia resulta justo y necesario explicar algunos conceptos importantes.

¿Qué es una malla?

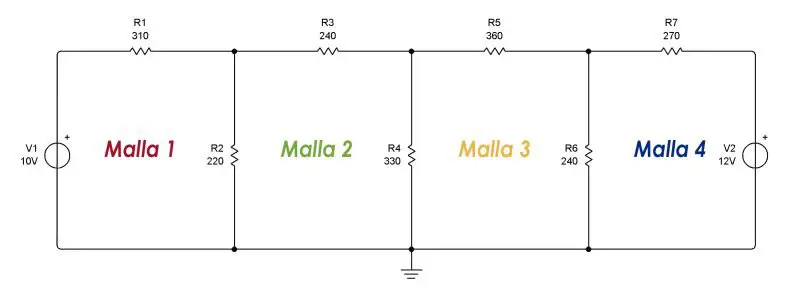
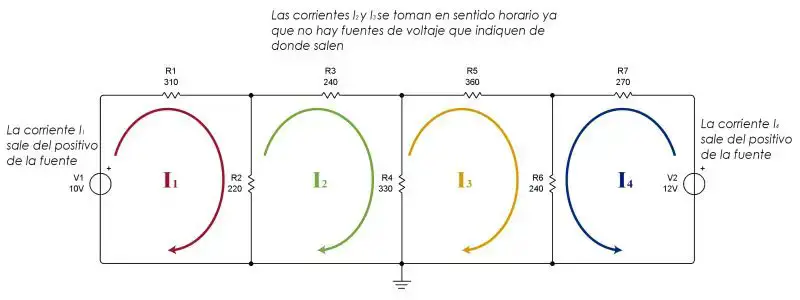
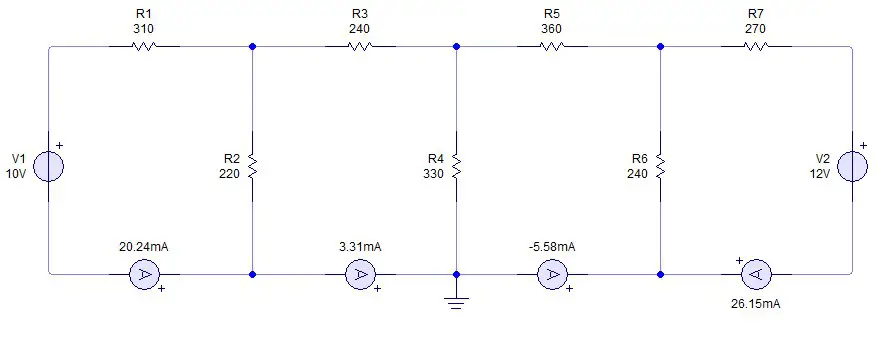
En un circuito eléctrico, una malla es un camino cerrado formado por elementos de circuitos. En el análisis de circuitos por mallas es imperativo identificar correctamente la cantidad de mallas en el circuito. Para el caso particular del circuito en la imagen se pueden identificar 4 mallas, formadas por 4 caminos cerrados.

Según la Ley de los Voltajes de Kirchhoff, la sumatoria de los voltajes en una malla es igual a cero. Recordemos que cuando una corriente pasa por un elemento de circuito, en este caso una resistencia se produce una diferencia de potencial. La Ley de Ohm establece que la diferencia de potencial (voltaje) en una resistencia es igual a la corriente multiplicada por la resistividad del elemento, es decir:

V=I·R

Si multiplicamos las corrientes de malla por cada resistencia en la malla, al sumar los voltajes el total debe ser cero. Para asumir las corrientes de malla, necesitamos tener en cuenta que en un circuito eléctrico la corriente sale del positivo de la fuente y entra por el negativo de la misma.

Si no hay una fuente de voltaje o de corriente en una malla entonces asumimos que la corriente fluye en un sentido horario. Se podría asumir en el sentido anti horario, lo cual no interesa mucho ya que si se escoge un sentido incorrecto la corriente que nos resultará al hacer nuestros cálculos tendrá signo negativo. Esto lo podremos apreciar al final cuando obtengamos nuestra respuesta.

Las corrientes las debemos representar en nuestro diagrama se la siguiente manera:

Vemos que en la malla 1 se asume que la corriente va en sentido horario ya que sale del positivo de la fuente. En las mallas 2 y 3 no hay fuente, así que se asume libremente (preferiblemente en sentido horario). En la malla 4 la corriente va en sentido anti horario por salir del positivo de la fuente de voltaje.

Luego de escoger el sentido de las corrientes, lo que sigue es colocar signos de polaridad a las resistencias por cada malla. Las resistencias no poseen polaridad pero para facilitar la resolución del problema le colocaremos signos. Una vez más debemos tomar en cuenta el sentido de la corriente: para todas las resistencias la terminal donde entra la corriente llevará un signo positivo. Donde sale la corriente de la resistencia se coloca un signo negativo.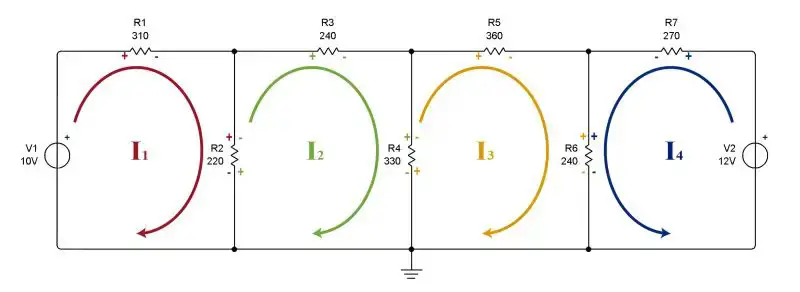

Ahora que hemos colocado los signos, se procede a establecer las ecuaciones para cada malla. Con la ayuda de los signos que hemos colocado se nos hace muy fácil hacer esto. Veamos.

Malla 1

En la malla 1 está pasando la corriente 1, por lo que es necesario multiplicar todas las resistencias por I1 para obtener los voltajes en las mismas. Se sumarán todos los voltajes en todas las resistencias más el voltaje de la fuente y la ecuación se igualará a cero.

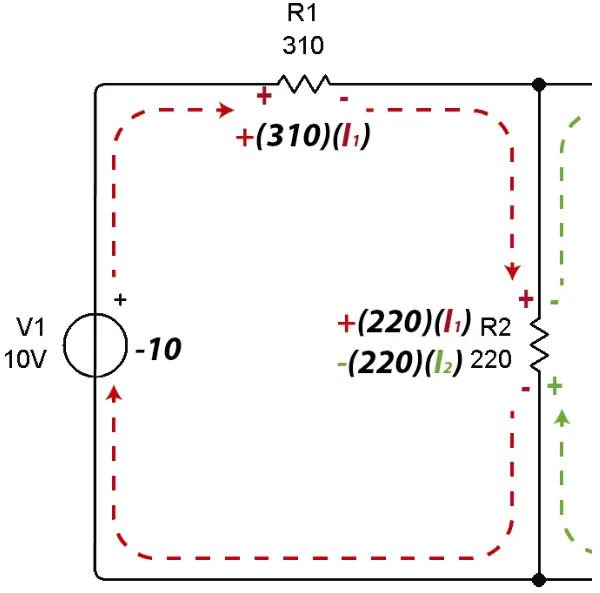
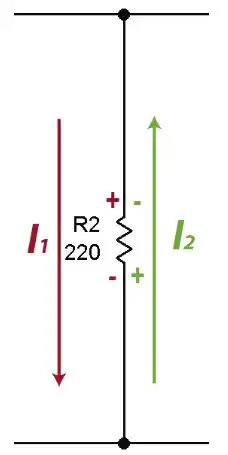
Nótese que por la resistencia R2 de 220 Ohm hay dos corrientes pasando, la corriente de la malla uno y la corriente de la malla 2.

Para esto se han colocado los signos sobre la resistencia. Como la corriente entra por el positivo en la malla 1, se toma el voltaje de la resistencia por efecto de I1 como positivo. En el mismo punto hay un signo negativo (en verde) en la malla 2 que indica que se debe restar el voltaje de la resistencia por efecto de I2.

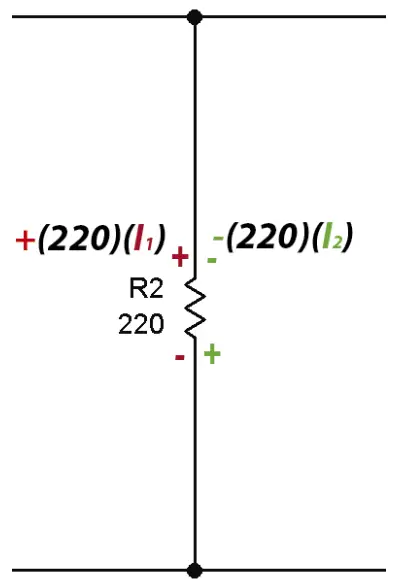
Al la ecuación que nos resulta es la siguiente:

Si reducimos la ecuación a su mínima expresión obtendremos la ecuación de voltajes de Kirchhoff para la Malla 1.

Ahora procedemos a hacer lo mismo para las mallas 2, 3 y 4.

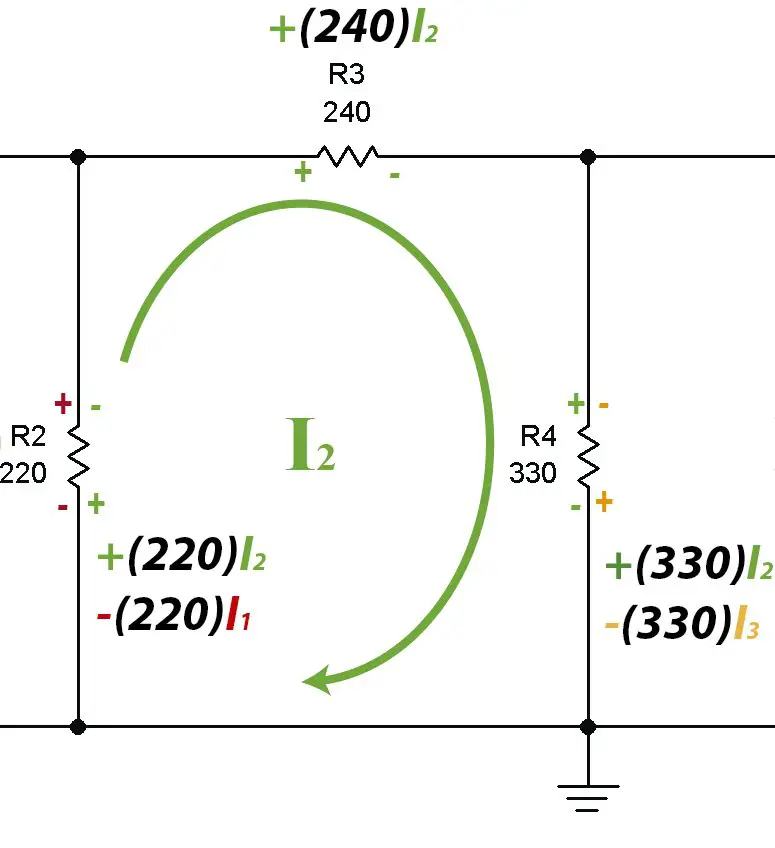
Malla 2

Reduciendo a su mí­nima expresión:

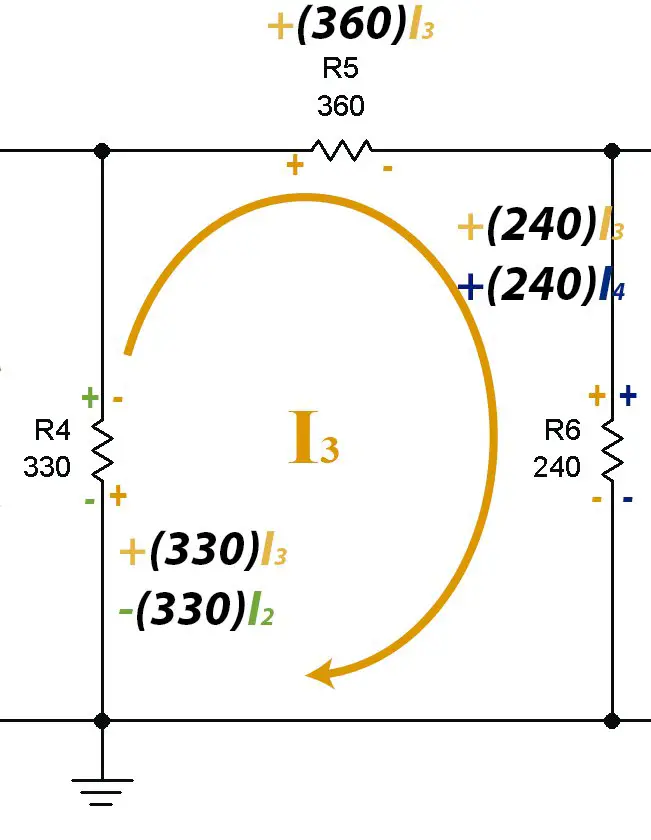
Malla 3

Como podemos observar, en la resistencia 6 los signos son positivo y positivo (++) por lo que se suma el voltaje en la resistencia provocado por I3 y el provocado por I4.

Al final la ecuación reducida es la siguiente:

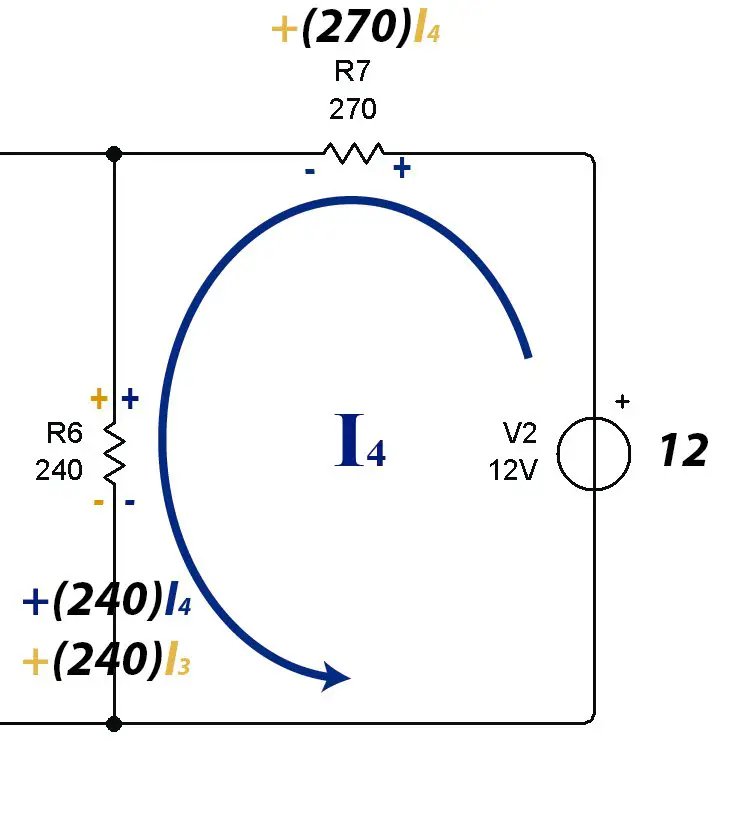
Malla 4

Reduciendo la ecuación a su más mínima expresión:

Resolviendo el sistema de ecuaciones

Una vez hayamos establecido las ecuaciones para cada malla tendremos un sistema de ecuaciones nxn donde n es el número de mallas. En este caso tenemos un sistema 4×4, es decir 4 ecuaciones con 4 incógnitas.

Esto nos permite utilizar cualquier método conocido para buscar los valores de las incógnitas. Puede ser por reducción, sustitución, determinantes, etc. Yo en lo personal utilizo matrices, especí­ficamente el método de Gauss Jordan.

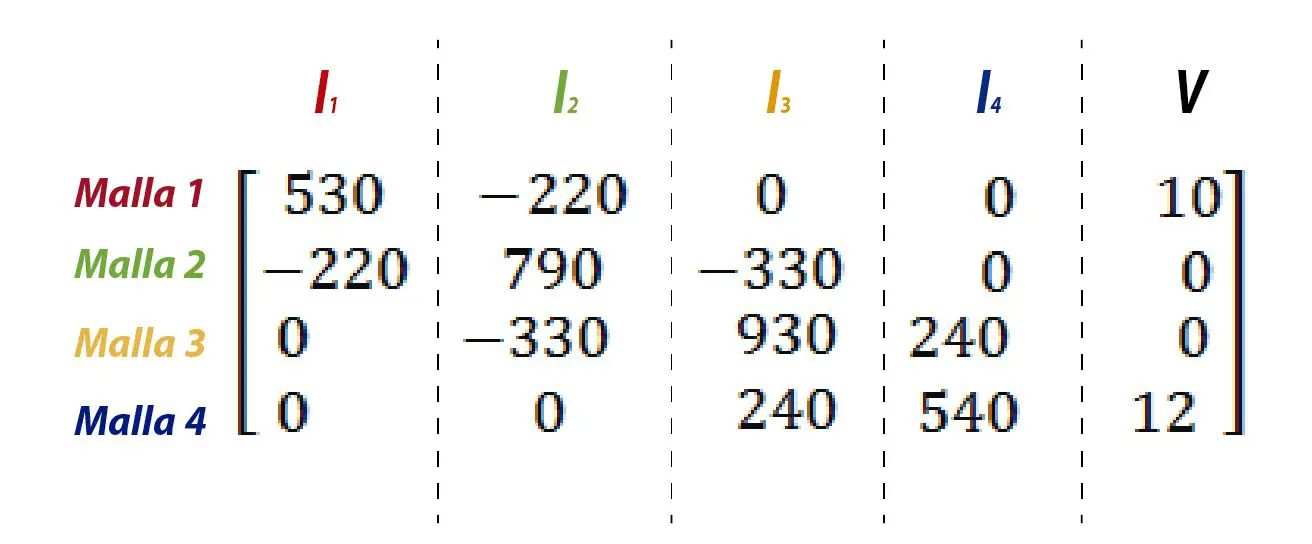
Para ello es necesario llevar todo el sistema a una matriz, donde en la primera columna irán los valores de I₁, en la segunda, tercera y cuarta irán I₂, I₃ e I₄ respectivamente. Por último el término libre, en este caso los voltajes irán en la última columna.

Ahora explicaré como resolver este sistema utilizando tres opciones diferentes, el Microsoft Mathematics, Matlab y Excel.

Microsoft Mathematics

El Mathematics es una excelente herramienta gratuita que proporciona Microsoft para nosotros los estudiantes. Se puede descargar gratuitamente desde la siguiente dirección:

Descargar Microsoft Mathematics

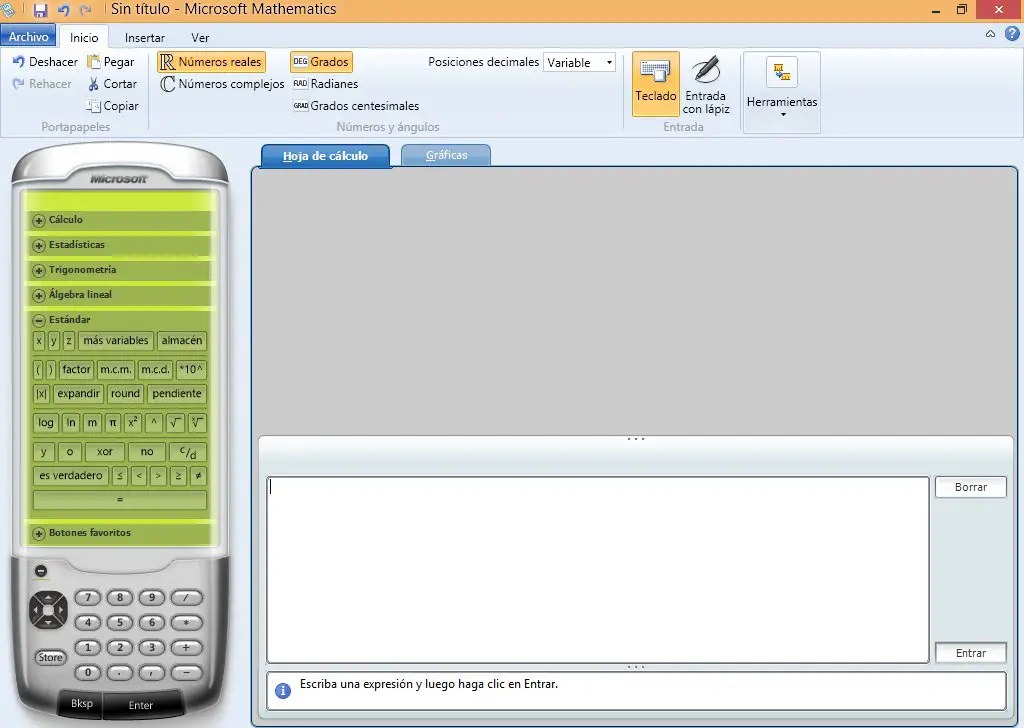
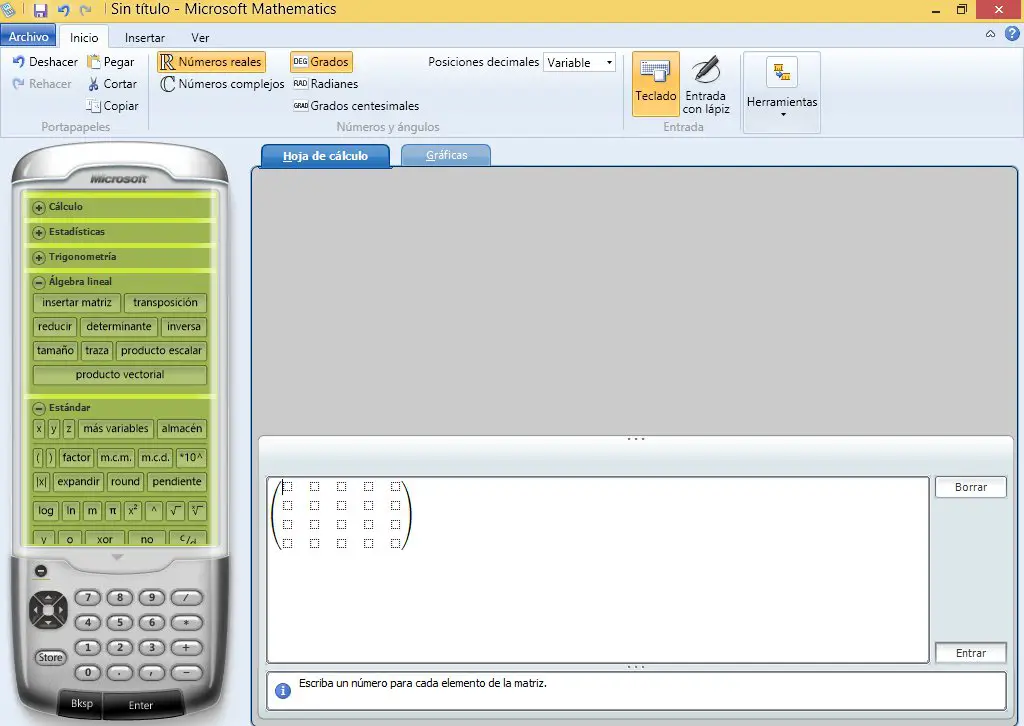
La interfaz es sencilla y fácil de usar.

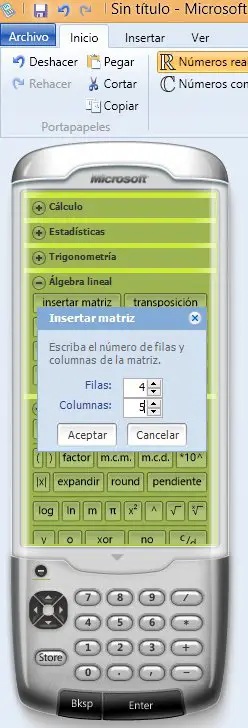
Ahora necesitamos insertar una matriz de n filas por n+1 columnas donde n es el número de mallas. En este caso sería una matriz de 4×5.

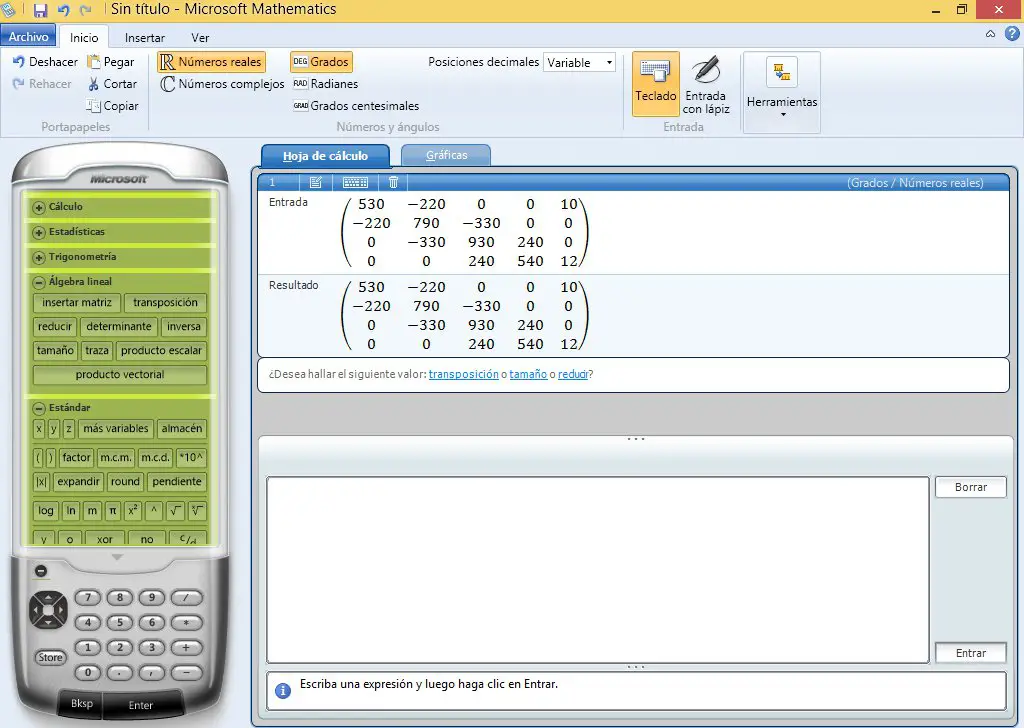
Ahora se introducen los datos:

Ahora se utiliza la opción reducir que nos aparece en la ventana.

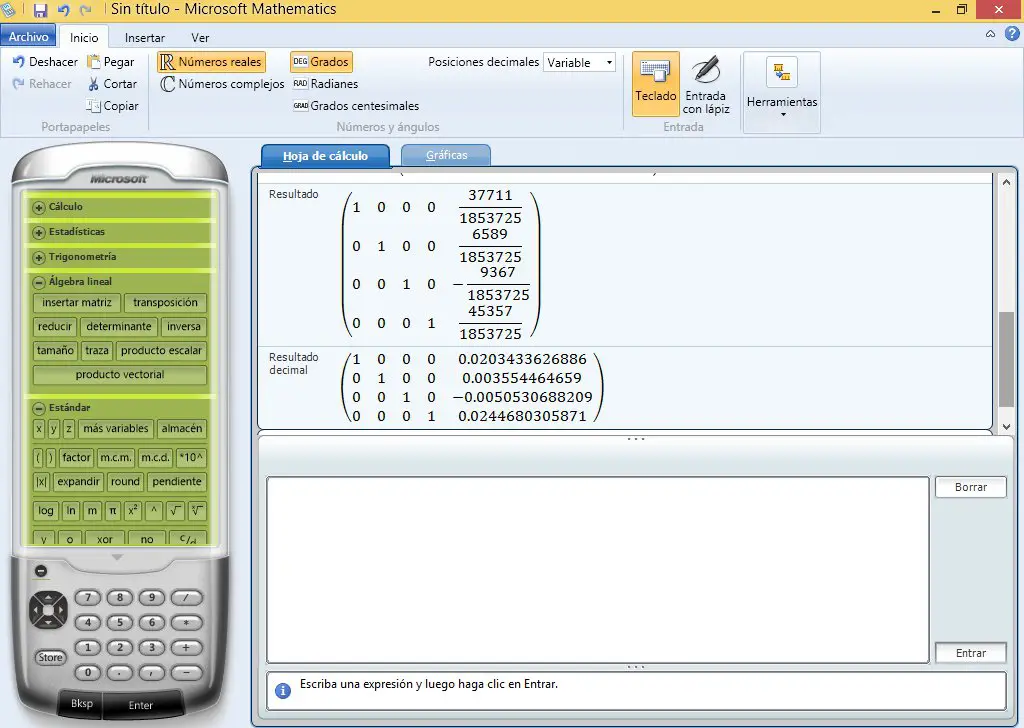
Nos aparecen los resultados en fracción y en decimal. Los números que se encuentran en la matriz reducida en la columna de la derecha serán los valores de las corrientes.

Será I1 20.3 mili amperios; I2 es 3.6 mili amperios; I3 es 5.06 mili amperios; I4 es 24.5 mili amperios.

El signo de I3 por ser negativo indica que a la hora de tomar el sentido de la corriente lo hicimos mal: I3 no va en sentido horario sino en sentido anti horario. El procedimiento está perfectamente correcto, solo tomamos mal el sentido. Al final el signo nos indica para dónde realmente va la corriente.

Ahora procedemos a comprobar si los resultados obtenidos son correctos. Veamos el simulador.

Los amperímetros en cada malla indican que el resultado obtenido en nuestros cálculos es correcto. En el simulador existen unas pequeñas pérdidas pero son insignificantes ya que estamos tratando con corrientes muy pequeñas.

Si utilizamos MatLab, el resultado obtenido debe ser similar.

Resolviendo el sistema de ecuaciones con Matlab

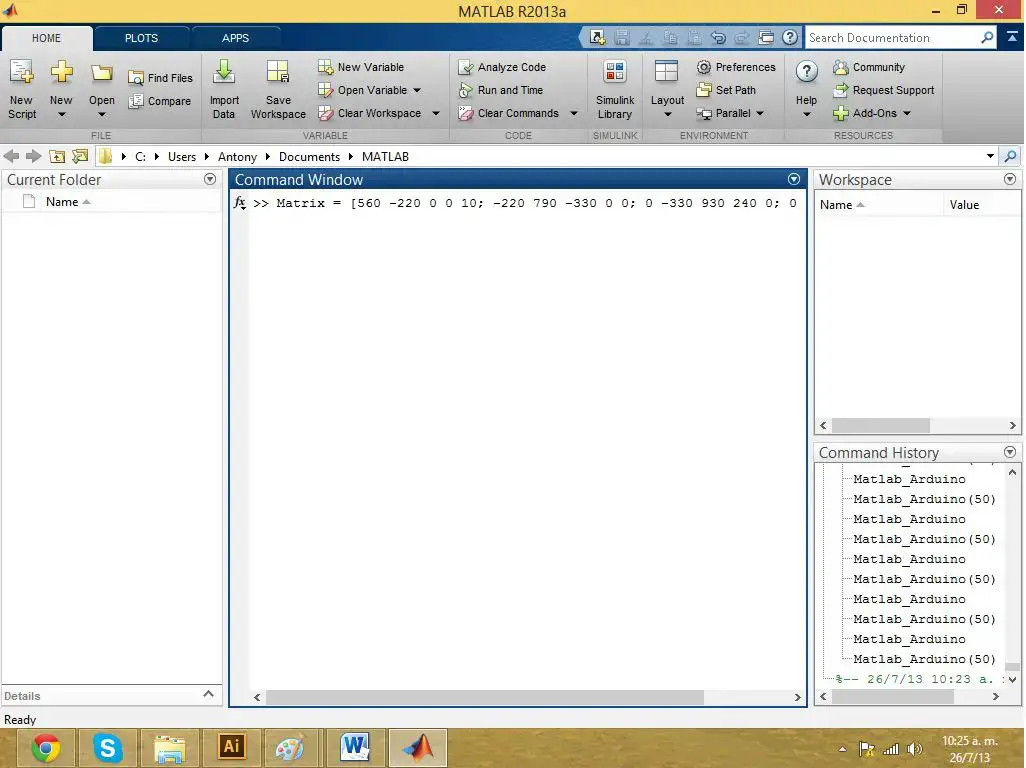
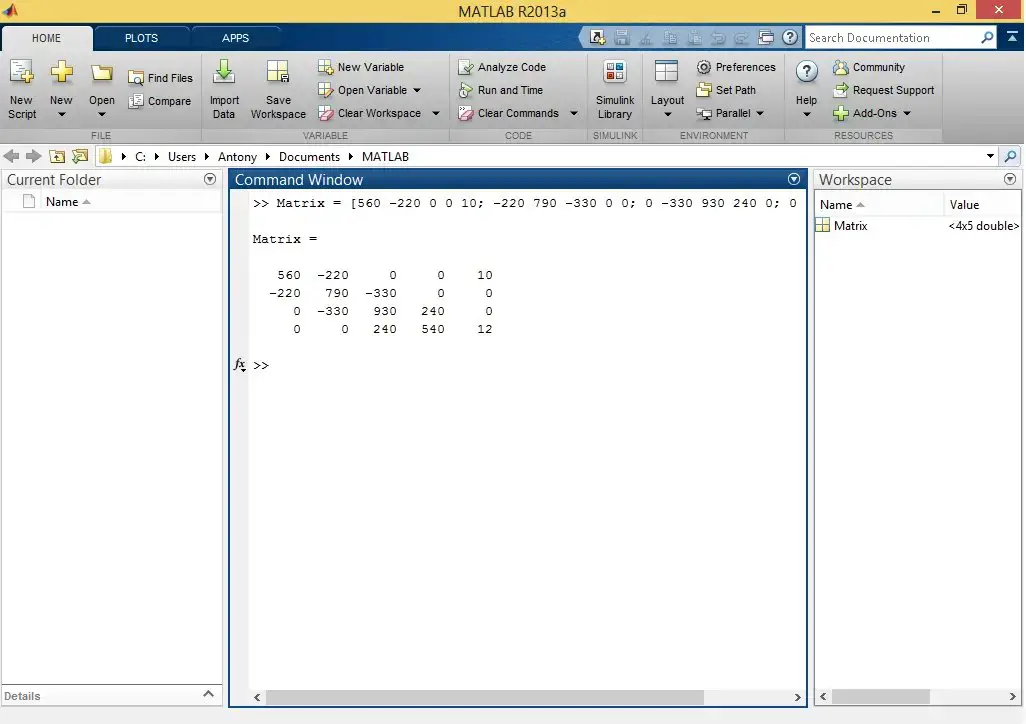
En Matlab declaramos la matriz con las ecuaciones de malla.

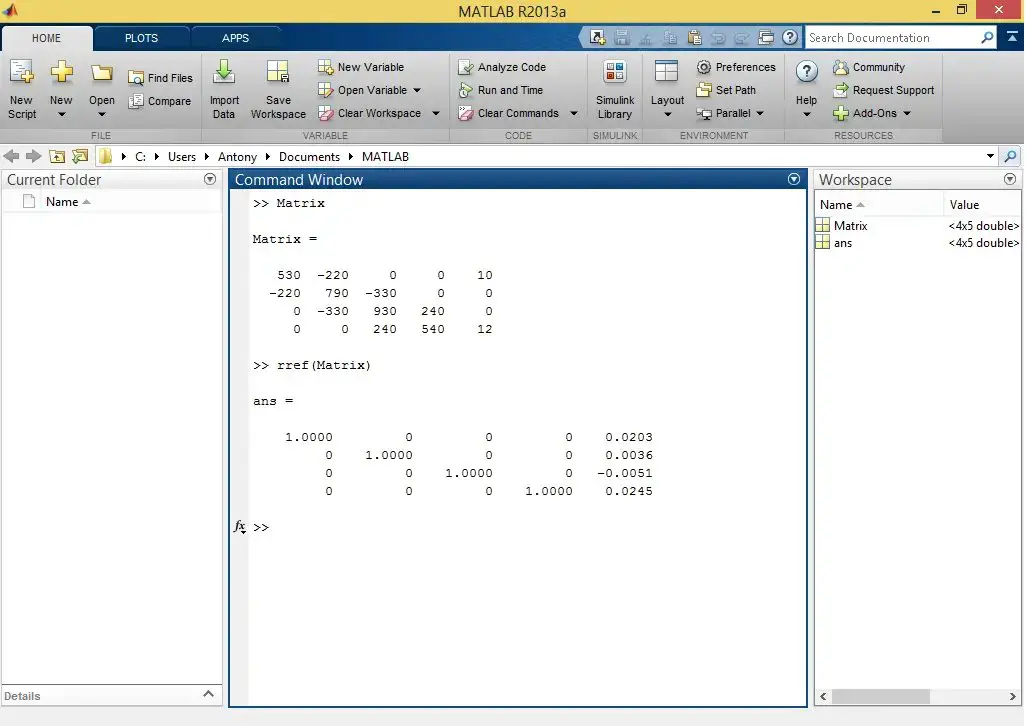
Ahora simplemente se aplica el comanto rref():

rref(Matrix)

Vemos que el resultado obtenido es muy similar al que nos entregó Microsoft Mathematics.

Microsoft Excel

Mi estimado amigo Secundino Villarreal, Ingeniero Electromecánico y docente de física en la Universidad Tecnológica de Panamá lanzó el sitio web excelparaingenieria.com en donde constantemente está publicando plantillas diseñadas en Excel. Hemos utilizado la plantilla Gauss Jordan: Ecuaciones Simultáneas 4 x 4 para resolver el sistema de ecuaciones de este ejemplo. La plantilla se encuentra disponible de forma gratuita en la web del autor. Cuando la descargamos veremos algo como esto:

Un poco más abajo encontraremos un cuadro donde ingresamos los valores de nuestras ecuaciones. La plantilla irá calculando automáticamente las respuestas del problema al hacer la reducción de Gauss-Jordan.

Como podemos observar, los resultados son iguales a aquellos obtenidos con Microsoft Mathematics y Matlab. El usuario puede escoger la forma como desea que los datos queden visualizados, ya sea en notación científica, fracciones, decimales, etc. Como ya mencioné, la plantilla la podemos descargar desde la web del autor.

Usted puede utilizar cualquier calculadora que pueda resolver sistemas de ecuaciones lineales para resolver el sistema. El método que se use la verdad no importa. Al final lo que determina si el problema está bien o mal es si se hace la sumatoria de los voltajes de forma correcta.

En el siguiente video muestro un resumen del contenido de este post, ahora utilizando una calculadora Texas Instruments Nspire CX CAS.

[youtube https://www.youtube.com/watch?v=eOdx-0wM_ds]

Conclusión

En Panama Hitek hemos creado una sección especial para compartir problemas resueltos de teoría de circuitos eléctricos. Los problemas resueltos poseen diferentes niveles de dificultad y han sido diseñados como exámenes para estudiantes de ingeniería eléctrica y carreras afines.

La Ley de los Voltajes de Kirchhoff es una ley fundamental en el análisis de circuitos eléctricos y electrónicos, y se utiliza en el análisis de circuitos por mallas. Esta ley establece que la suma de los voltajes en una malla, o camino cerrado en un circuito eléctrico, debe ser igual a cero.

Para calcular las corrientes de malla en un circuito, se pueden usar diferentes métodos, como el análisis de nodos o el método Zbus, y también existen otros métodos como la superposición, la transformación de fuentes, el análisis matricial y los teoremas de Thévenin y Norton.

Es importante tener en cuenta que en un circuito eléctrico la corriente fluye del positivo a la negativo de la fuente y que en ausencia de una fuente, se suele asumir que la corriente fluye en sentido horario.

Espero que este post haya sido útil para entender la Ley de los Voltajes de Kirchhoff y su aplicación en el análisis de circuitos por mallas. Si tienen alguna duda o comentario, no duden en dejar un mensaje en los comentarios. ¡Gracias por leer!