It’s been a while since my last Java programming post. I’ve been focusing on Python and Machine Learning tutorials recently, but Java remains my favorite programming language.
Random number selection with weighted probabilities is a common task in programming, especially when working with data that has a specific probability distribution. For example, you may have a list of letters with different probabilities of being selected, or a list of items with different probabilities of being chosen from a menu. In this post, we will explore how to implement a solution for this problem in Java using a simple and intuitive approach.
Random number selection
A random number is a number that is generated by a computer program or a hardware random number generator in a way that is unpredictable and does not follow a deterministic pattern. The purpose of generating random numbers is to provide a means of introducing an element of chance into a computer program or system.
There are many different ways to generate random numbers, and the quality and characteristics of the random numbers generated can vary significantly depending on the method used. In general, however, a good random number generator should produce numbers that are uniformly distributed over a wide range, are statistically independent of one another, and are not easily predictable.
To generate a random number in Java, you can use the java.util.Random class. For example, the following code generates a random number between two numbers:
|
1 2 3 4 |
Random random = new Random(); int min = 0; int max = 10; int randomNumber = random.nextInt(max - min + 1) + min; |
This code generates a random integer between 0 and 10, inclusive. Each number has an equal probability of being chosen. To test this algorithm, we are going to create a simple proof-of-concept test.
Generating Random Numbers with Equal Probability
To test the code above, I am going to create a testing script. The code I am going to present here can be found in our Github repository.
The first thing I am going to do is to declare a class with the following attributes:
|
1 2 3 4 5 6 7 8 9 10 11 12 |
private static class Letters { private String letter; private int count; private double probability; public Letters(String letter, int count, double probability) { this.letter = letter; this.count = count; this.probability = probability; } } |
This class makes possible to create objects with letters, a counter and an specific probability. Now I am going to create a list of 10 letters:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
// Create a list of letters List<Letters> letters = new ArrayList<>(); // Add 10 letters to the list with their corresponding count and probability letters.add(new Letters("A", 0, 0.2)); letters.add(new Letters("B", 0, 0.2)); letters.add(new Letters("C", 0, 0.1)); letters.add(new Letters("D", 0, 0.1)); letters.add(new Letters("E", 0, 0.1)); letters.add(new Letters("F", 0, 0.1)); letters.add(new Letters("G", 0, 0.05)); letters.add(new Letters("H", 0, 0.05)); letters.add(new Letters("I", 0, 0.05)); letters.add(new Letters("J", 0, 0.05)); |
To randomly select a letter, I created this method:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
/** * Method for performing selection tests with non-weighted probability. * * @param letters list of letters to perform tests on * @param testCount number of tests to perform */ private static void nonWeightedProbability(List<Letters> letters, int testCount) { for (int i = 0; i < testCount; i++) { // Generate random number between 0 and size of letters list minus 1 Random random = new Random(); int min = 0; int max = letters.size() - 1; int randomNumber = random.nextInt(max - min + 1) + min; // Select letter at index of random number and increment its count by 1 String selectedLetter = letters.get(randomNumber).getLetter(); letters.stream() .filter(a -> a.getLetter().equals(selectedLetter)) .findFirst() .ifPresent(l -> l.setCount(l.getCount() + 1)); } // Print count and percentage of each letter for (Letters letter : letters) { System.out.println(letter.getLetter() + " -> " + letter.getCount() + "(" + String.format("%.2f", (letter.getCount() * Math.pow(testCount, -1)) * 100) + "%)"); } // Reset count of each letter to 0 letters.forEach(a -> a.setCount(0)); } |
The method performs a loop “testCount” number of times. In each iteration of the loop, it generates a random integer between 0 and the size of the “letters” list minus 1. Then, it selects the “Letter” object at the index of the random number and increments its count by 1.
After the loop finishes executing, the method prints out the count and percentage of each “Letter” object. Finally, it resets the count of each “Letter” object to 0.
To test this code, you need to make something like this:
|
1 2 |
int testCount = 100000; nonWeightedProbability(letters, testCount); |
The following output is produced after running the random letter selection 100,000 times:
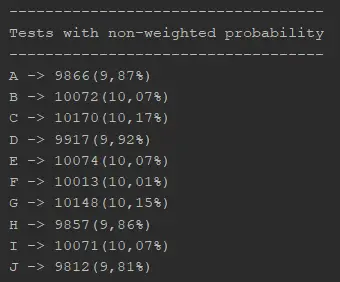
As we can see, each letter has been selected approximately 10% of the time, with the results fluctuating slightly above or below this value. This demonstrates that the random letter selection process is generating output with equal probability for each letter.
Generating Random Numbers with Weighted Probability in Java
Sometimes we may want to generate random numbers with probabilities that are not all equal. For example, we may want one letter to be selected more frequently than the others. In these cases, we can use weighted probabilities. This allows us to specify the probability of selecting a particular element, rather than all elements having an equal probability of being selected.
In the letter list that I created before I assigned a probability for each letter:

Now, we will create a method similar to the previous one, but the resulting percentages for each letter should be close to the probabilities that were set. Here is the method:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
/** * * Method for performing selection tests with weighted probability. * * @param letters list of letters to perform tests on * @param testCount number of tests to perform */ private static void weightedProbability(List<Letters> letters, int testCount) { //Repeat the selection process 'testCount' times for (int i = 0; i < testCount; i++) { //List to hold the cumulative probabilities of each letter List<Double> cumulativeProbabilities = new ArrayList<>(); double sum = 0; //Calculate cumulative probabilities for each letter for (Letters l : letters) { sum += l.getProbability(); cumulativeProbabilities.add(sum); } //Generate a random number between 0 and 1 double r = Math.random(); //Select a letter based on the cumulative probabilities String selectedLetter = letters.stream() //Find the first letter whose cumulative probability is greater than the random number .filter(l -> r < cumulativeProbabilities.get(letters.indexOf(l))) .findFirst().get().getLetter(); //Increment the count for the selected letter letters.stream() .filter(a -> a.getLetter().equals(selectedLetter)) .findFirst() .ifPresent(l -> l.setCount(l.getCount() + 1)); } //After 'testCount' loops, print out the number of times each letter was selected and the percentage it represents for (Letters letter : letters) { System.out.println(letter.getLetter() + " -> " + letter.getCount() + "(" + String.format("%.2f", (letter.getCount() * Math.pow(testCount, -1)) * 100) + "%)"); } //Reset the count for each letter to 0 letters.forEach(a -> a.setCount(0)); } |
The result of running this code is:
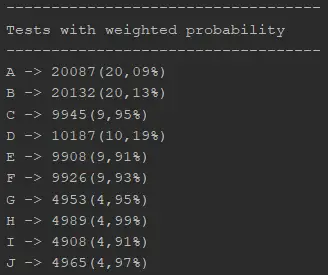
As seen in the output, the selection frequency for each letter aligns with the probability that was previously set. This demonstrates that our algorithm effectively functions as a weighted random number generator.
Conclusion
The complete code with both examples can be downloaded from our Github Repository.
In conclusion, we have learned how to generate random numbers with equal probability and with weighted probability in Java using the java.util.Random class. We have also seen how to implement a random selection algorithm with weighted probabilities using a list of objects with a letter, a counter and a probability attribute.
We hope that this post has been helpful to you and if you have any questions or comments, please don’t hesitate to leave them below. Thank you for reading!



