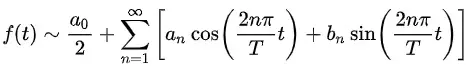Este es un post que había querido escribir hace mucho tiempo, pero es hasta ahora que tengo el tiempo, la disposición y el estado mental apropiado para compartir mis ideas y conocimientos sobre este tema. En esta publicación trataré de explicar lo que yo considero son los dos principales métodos para el análisis de circuitos con fuentes de poder en corriente alterna: Transformada de Laplace y Frecuencia Compleja.
Se trata de un post un poco extenso dada la cantidad de conceptos que debo definir antes de entrar en materia. Después, en publicaciones separadas, haré énfasis en técnicas de análisis en corriente alterna, específicamente el análisis por mallas, análisis por nodos y, probablemente, análisis matricial.
Antes de entrar en materia me gustaría aclarar que este post presentará una complejidad matemática importante. Como ingeniero que soy, mi fuerte nunca ha sido el álgebra o las matemáticas en general, sino la aplicación de distintos tipos de modelos matemáticos para describir el comportamiento de toda clase de fenómenos físicos.
Para resolver las ecuaciones utilizaré el simulador de la TI-Nspire CX CAS, una de las calculadoras de Texas Instruments. Esta máquina me acompañó durante mis estudios de licenciatura, en maestría y ahora en el doctorado. Mi fiel compañera.
Dicho esto, empecemos.
La función excitatriz
Las veces que me ha tocado dictar el curso de Circuitos II en la Universidad he iniciado explicando el concepto de la función excitatriz. Este es un modelo matemático que nos permite describir cualquier tipo de fuente de poder, sea de voltaje o de corriente, en un circuito eléctrico. Para mi, entender este concepto resulta fundamental.
El modelo matemático es el siguiente:
Donde:
-
- v(t) es el valor de la función excitatriz en cualquier tiempo
- Vm es la amplitud máxima de la función
- t es el tiempo, dado en segundos
- σ es la frecuencia neperiana, dada en nepers por segundo
- ω es la frecuencia angular, dada en radianes por segundo
- φ es el ángulo de desfase de la función
Modificando estos parámetros es posible construir cualquier forma de onda utilizada en circuitos eléctricos, ya sea como fuentes de voltaje o fuentes de corriente. Por ejemplo:
Si consideramos que σ=0, ω=0 y φ=0, tendremos una función constante, tal como el de las fuentes de poder de corriente directa (DC):
Si consideramos que σ≠0, ω=0 y φ=0 tendremos una función exponencial:
Si consideramos que σ=0, ω≠0 y φ≠0 tendremos una función cosenoidal:
Cabe destacar que una función coseno puede ser transformada en una función seno modificando el valor de φ (específicamente con un atraso de 90º). La función excitatriz es, de por si, una función senoidal amortiguada, lo cual se puede lograr cuando tenemos valores distintos de cero en las dos frecuencias de la función.
Cuando hablo de este tema en con mis estudiantes me gusta preguntarles: ¿cómo hacemos para modelar funciones de onda cuadrada, dientes de sierra o similares? Pues para ello en ingeniería estudiamos un procedimiento que nos permite modelar funcionas periódicas como una suma de funciones senoidales: la Serie de Fourier.
Por ejemplo, supongamos que queremos construir un modelo matemático que reproduzca la siguiente señal:
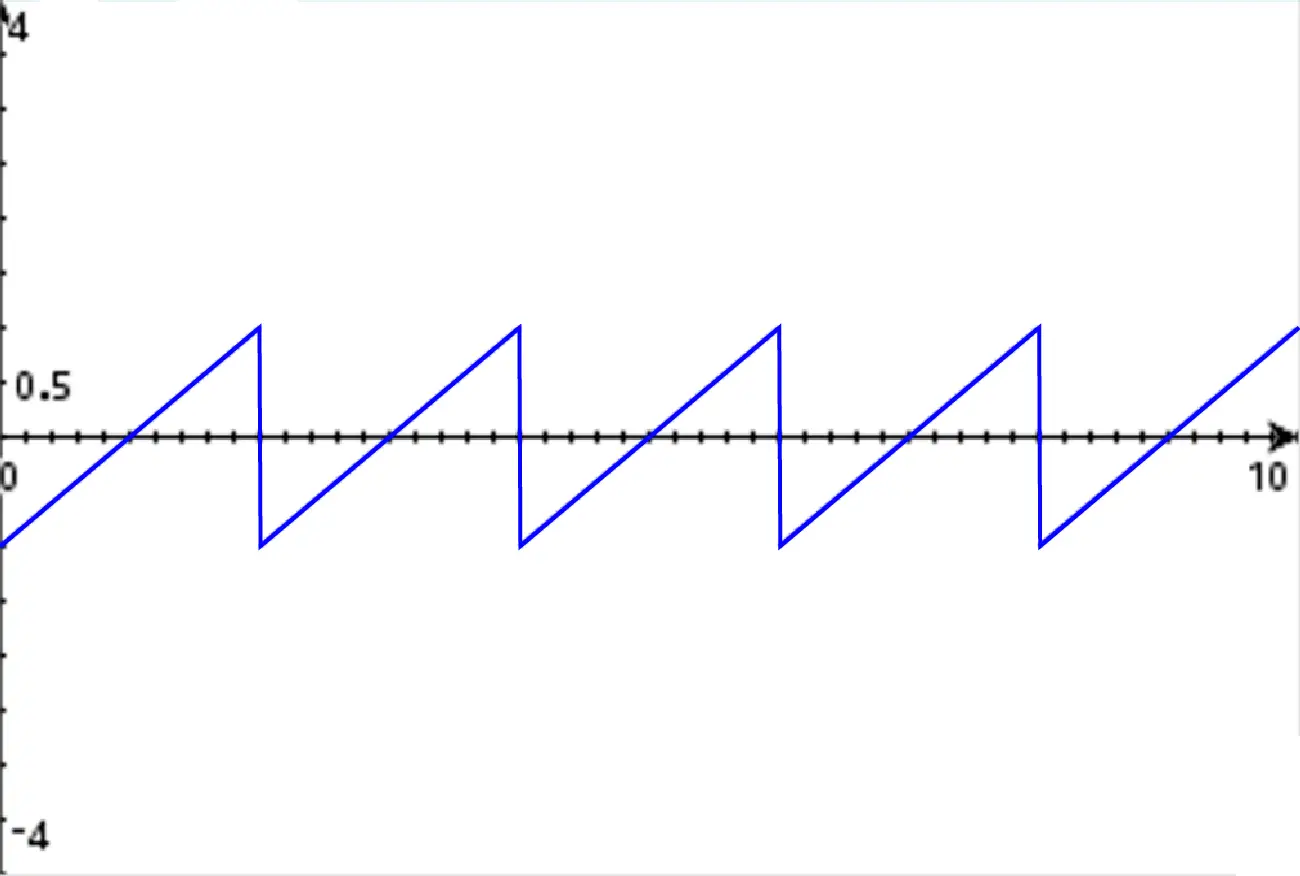
Es una señal diente de sierra. La Serie de Fourier nos permite construir una señal como esa a partir de senos y cosenos, utilizando el siguiente modelo matemático:
Donde:
Si utilizamos este modelo para modelar la señal diente de sierra de la imagen de más arriba, el procedimiento sería:
Si le asignamos un valor a la «m» de la sumatoria le estamos indicando cuantos armónicos queremos producir. A esto se le conoce como la expansión de la Serie de Fourier. Cuando expandimos la serie, lo que nos queda es una suma de senos y cosenos:
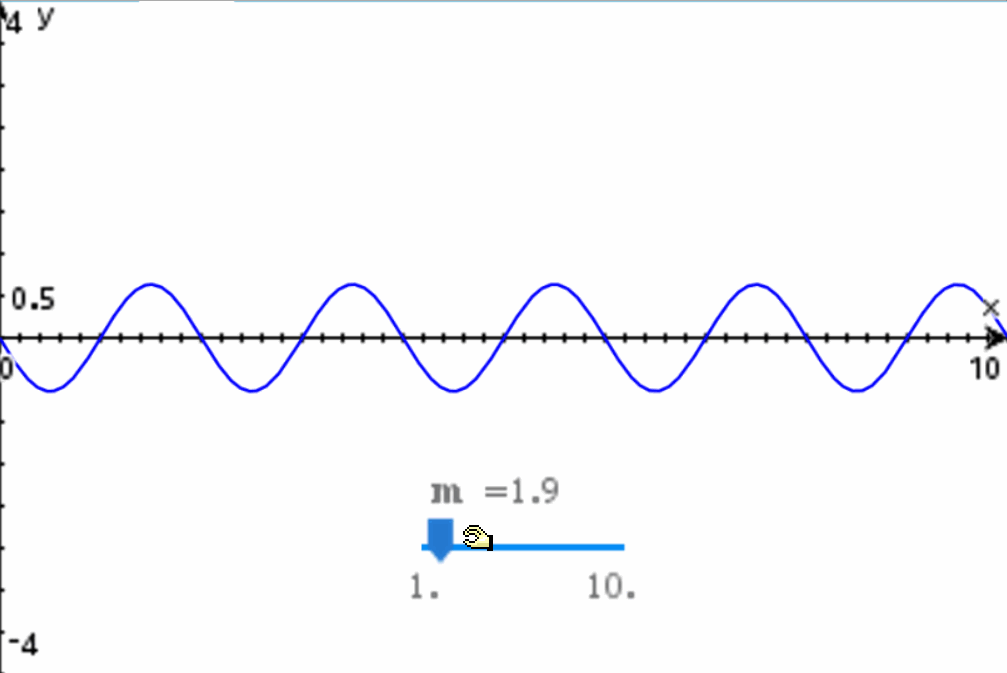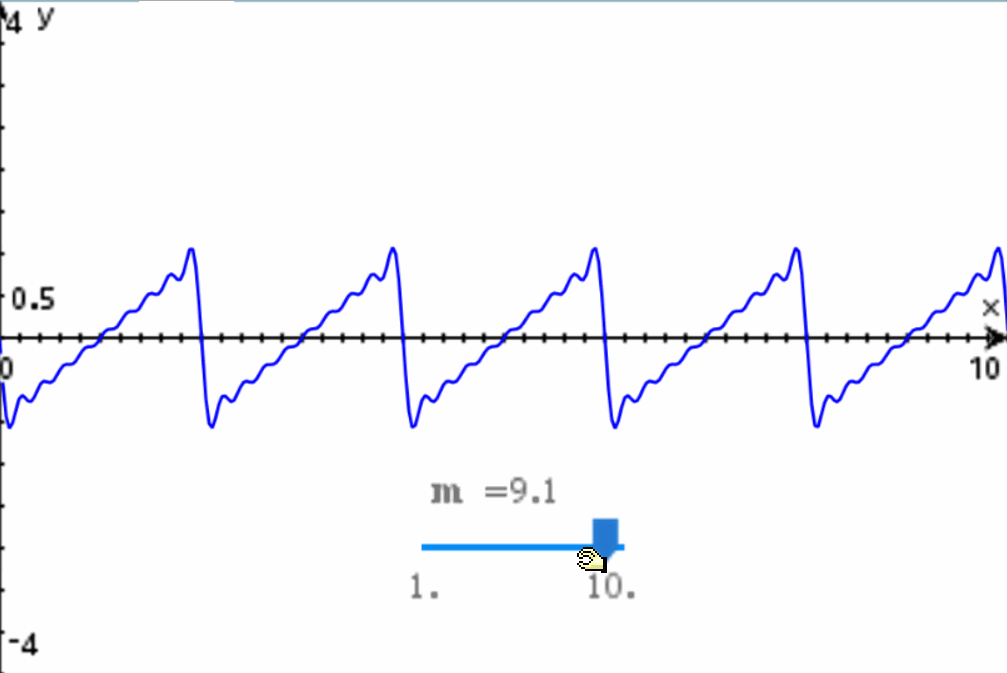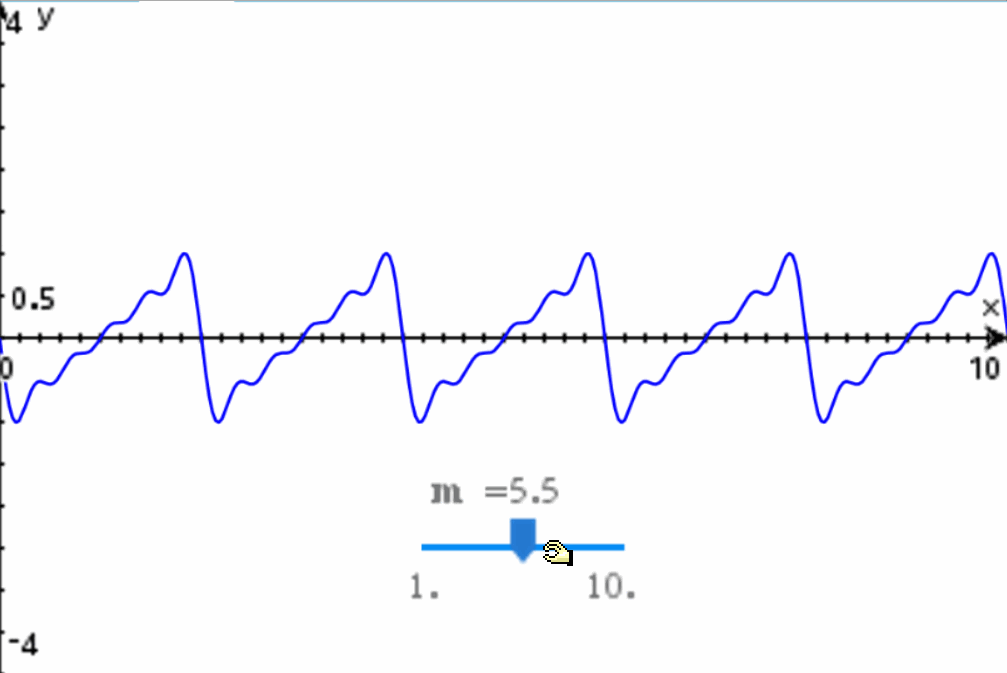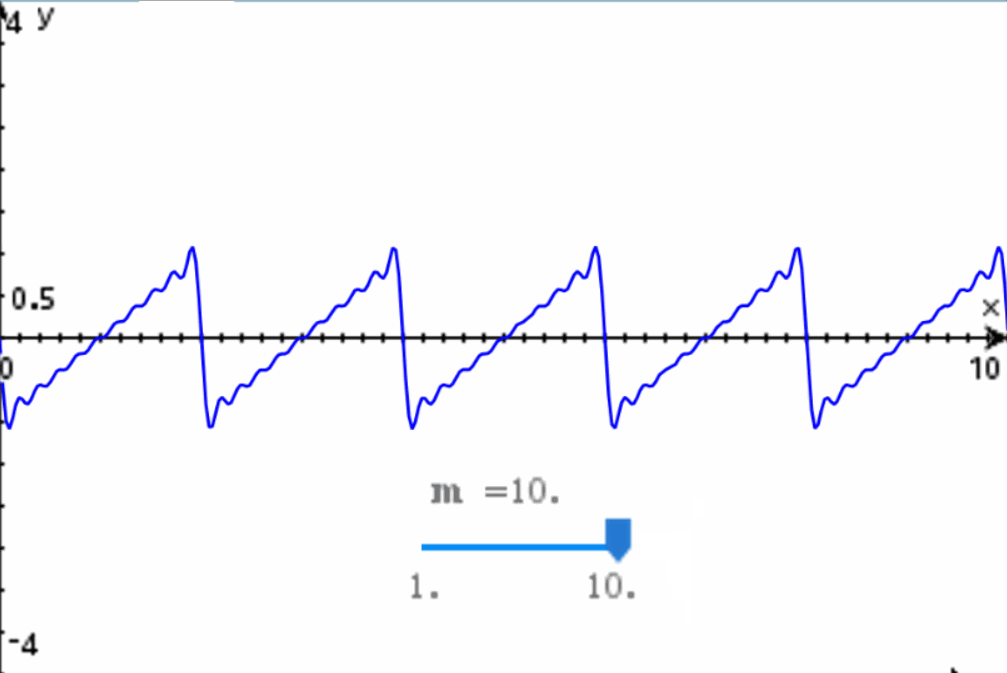
Como vemos, hemos especificado que queremos una expansión de 10 armónicos. El resultado de la expansión son 10 funciones senoidales, las cuales se ajustan al modelo general de la función excitatriz que hemos presentado aquí. Si graficamos la expansión de la Serie de Fourier, el resultado es:
Como vemos, al agregar más armónicos a la expansión de la Serie de Fourier se logra que el modelo matemático poco a poco se ajuste a la onda diente de sierra que queríamos modelar en un principio. Entre más armónicos se utilicen, más fiel será la onda a la forma deseada:
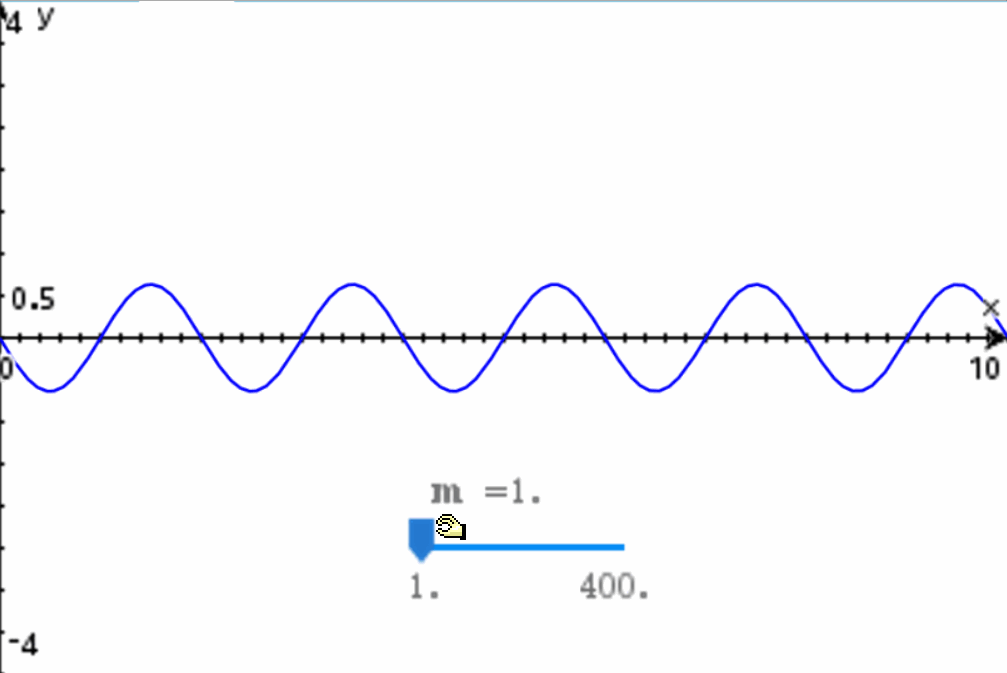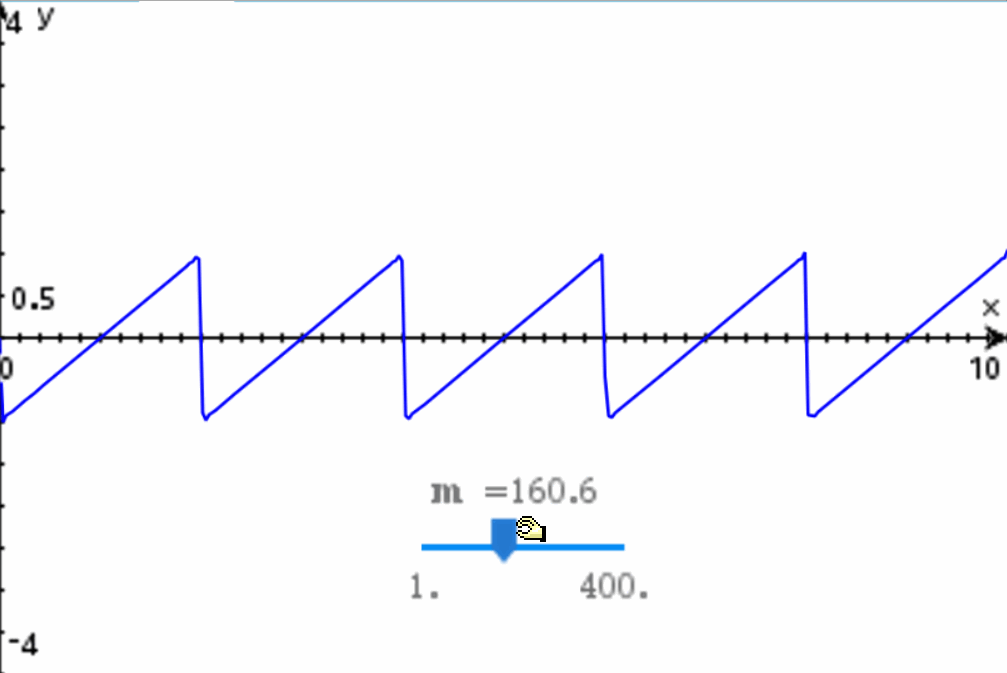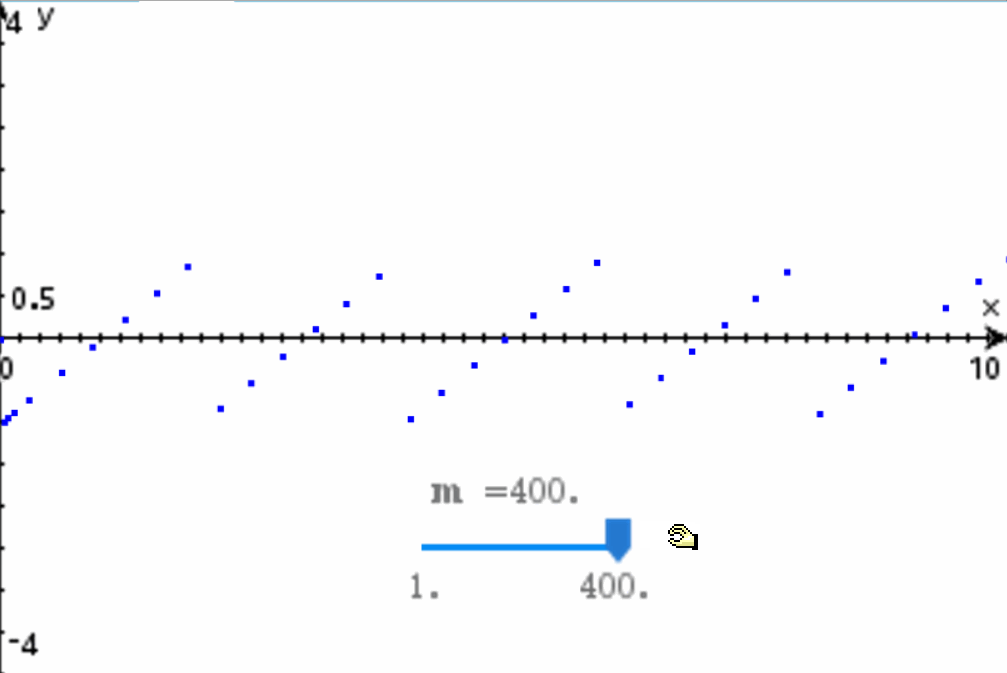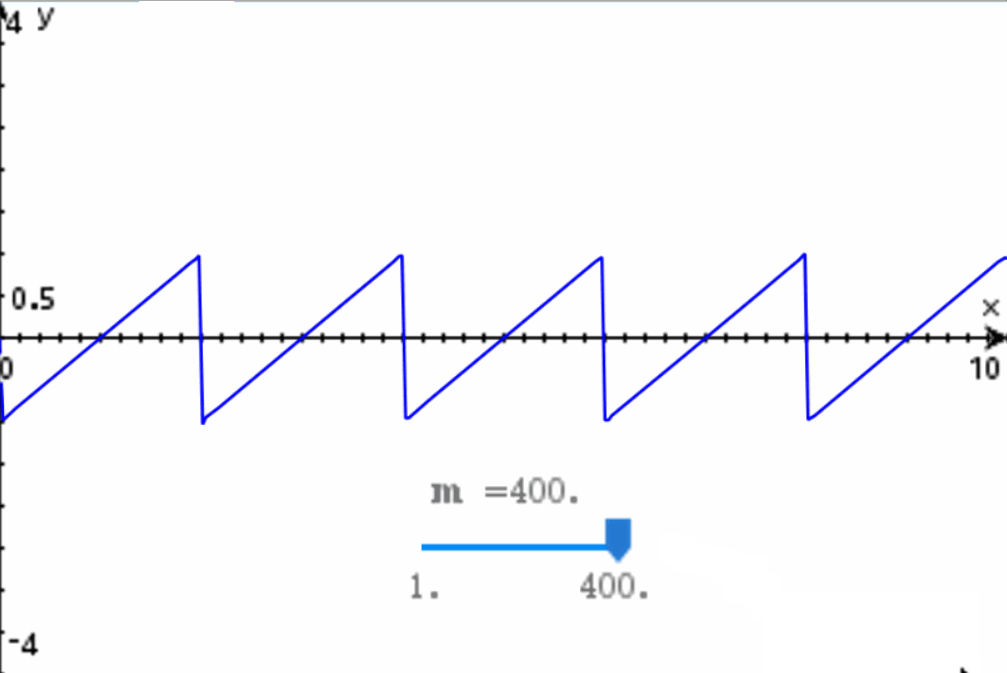Independientemente de la cantidad de armónicos que se necesiten, con la función excitatriz (o la suma de funciones) podemos describir cualquier onda periodica. También podemos modelar ondas no periodicas, utilizando funciones tipo escalón unitario o jugando con la frecuencia neperiana del modelo matemático.
Sea como sea, es imperativo entender la función excitatriz y su importancia en el análisis de circuitos eléctricos.
Sistema de ecuaciones integro-diferenciales
Lo que dificulta el análisis de circuitos eléctricos en corriente alterna no es la función excitatriz, sino la presencia de elementos reactivos, específicamente inductores y capacitores.
Por ejemplo, supongamos que tenemos el siguiente circuito eléctrico:
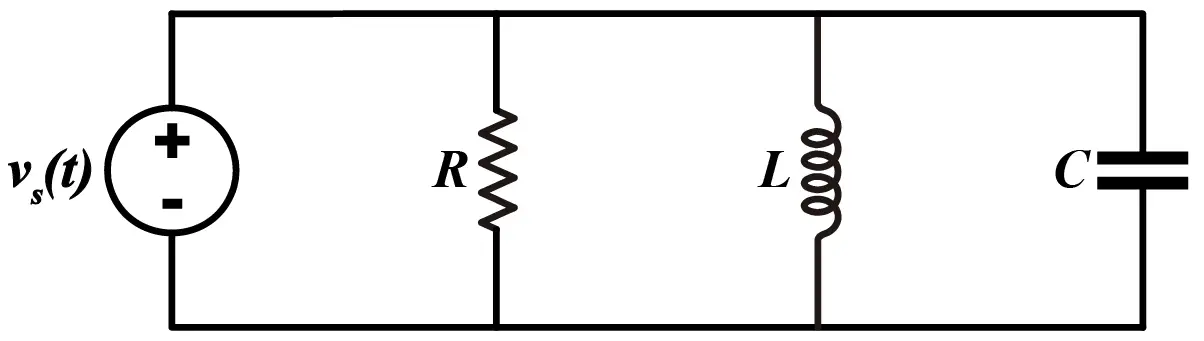
Supongamos que queremos conocer la corriente entregada por la fuente de poder vs(t) en el dominio del tiempo. Según la Ley de Corrientes de Kirhhoff, esta corriente será la suma de las 3 corrientes, la de la resistencia, el inductor y el capacitor. Esto lo podemos expresar de la siguiente manera:
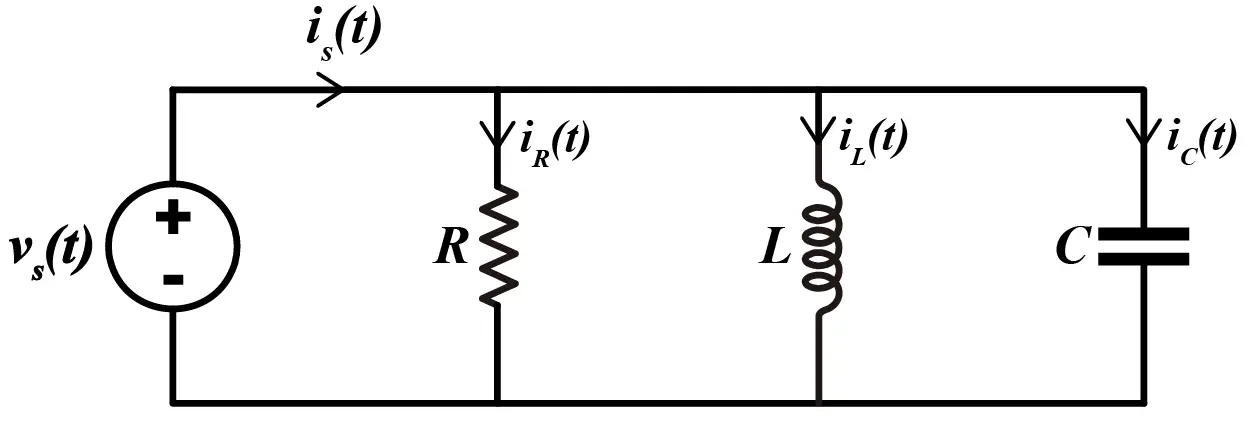
En el caso de la resistencia, la corriente la podemos calcular fácilmente utilizando la Ley de Ohm. En el caso de el inductor y el capacitor, cada uno tiene un modelo matemático para el cálculo de corriente en función del tiempo.
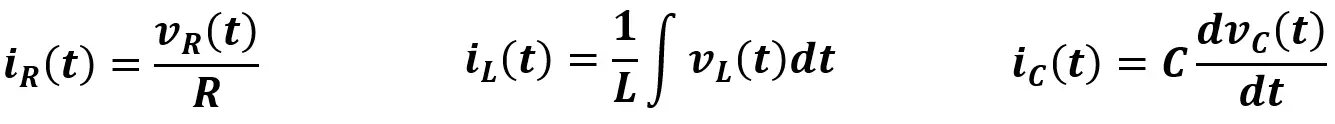
Como los tres elementos están conectados en paralelo a la fuente de poder, el voltaje en cada elemento será igual al voltaje de la fuente de poder. Dicho esto, la corriente entregada por la fuente de poder queda definida como:
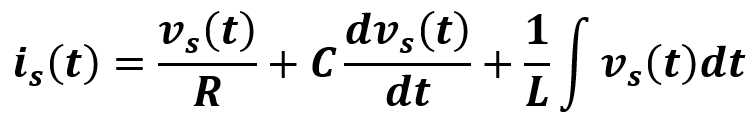
Esta es una ecuación integro diferencial, es decir, con integrales y derivadas en una misma expresión. Para un matemático probablemente no resulta muy difícil resolver la derivada y la integral en esta expresión y obtener la expresión que representa la corriente entregada por la fuente. En ingeniería te enseñan a trabajar con este tipo de expresiones en un curso llamado Ecuaciones Diferenciales y Ordinarias. Desde este punto de vista pareciera que el problema no es tan complicado.
Sin embargo, ¿qué pasa cuando necesitamos encontrar la respuesta a varias incógnitas? ¿un sistema de ecuaciones integrodiferenciales simultáneas?. Ese es precisamente el problema al que nos enfrentamos cuando analizamos circuitos eléctricos con múltiples mallas, múltiples nodos y múltiples fuentes de poder.
Transformación de modelos matemáticos del dominio del tiempo al dominio de la frecuencia
Cuando tenemos expresiones matemáticas difíciles de resolver en el dominio del tiempo resulta muy conveniente trabajar en el dominio de la frecuencia. Básicamente lo que hacemos es aplicar Transformada de Laplace a los modelos matemáticos en función del tiempo de cada uno de los elementos. Luego pasamos a resolver el álgebra en el dominio de la frecuencia, para finalmente volver al dominio del tiempo, ya sea con una Transformada Inversa de Laplace o con un método aproximado, como Frecuencia Compleja.
Existen otras opciones para análisis de circuitos en corriente alterna, como la Transformada de Fourier, pero en este post nos concentraremos en los métodos previamente mencionados: Frecuencia Compleja y Transformada de Laplace.
Cuando se trabaja con la Transformada de Laplace se suele utilizar una tabla de Transformadas para convertir distintos tipos de modelos matemáticos en el dominio del tiempo a su equivalente en el dominio de la frecuencia. En análisis de circuito las transformadas que más utilizamos son:
Como vemos, las derivadas se transforman en «s» y las integrales en «1/s». De esta forma resulta muy sencillo hacer análisis de circuitos, pues ya no es necesario lidiar con integrales ni derivadas. En ambos casos existen términos asociados a las condiciones iniciales del circuito, pero en este post consideraremos que los inductores y capacitores están descargados. Más adelante espero hacer un post en el que explicaré el procedimiento utilizado para analizar circuitos con condiciones de carga inicial.
En la siguiente tabla estoy compartiendo con ustedes los modelos matemáticos para la resistencia, inductor y capacitor en el dominio del tiempo y su equivalente en el dominio de la frecuencia.
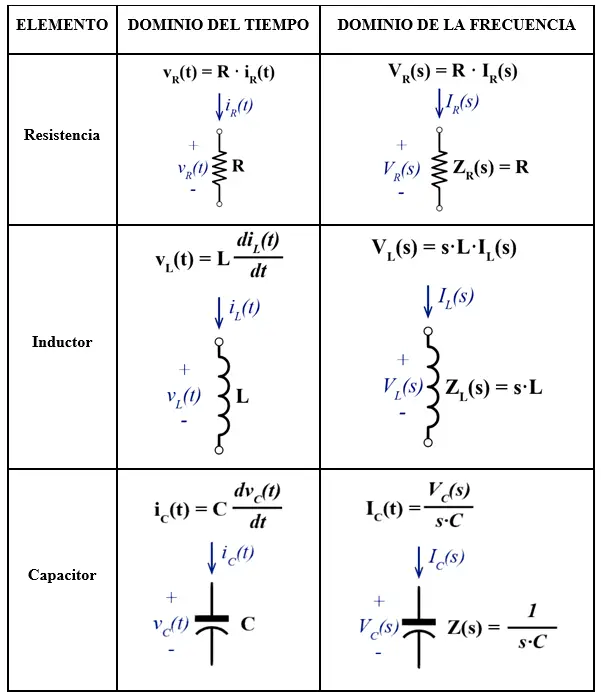
Creo que la mejor manera de ilustrar el uso de esta tabla es resolviendo un ejemplo. Vamos a ello.
Análisis de circuitos en el dominio de la frecuencia
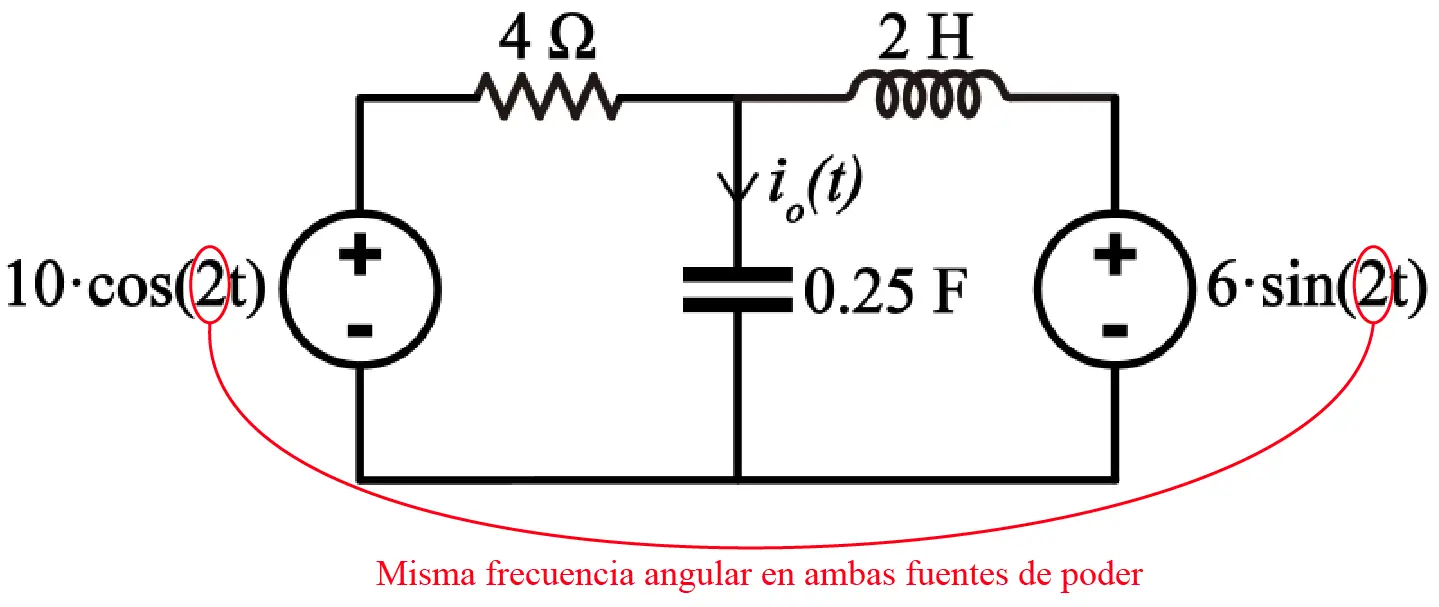
Para ilustrar el análisis de circuitos en el dominio de la frecuencia utilizaremos el siguiente circuito:
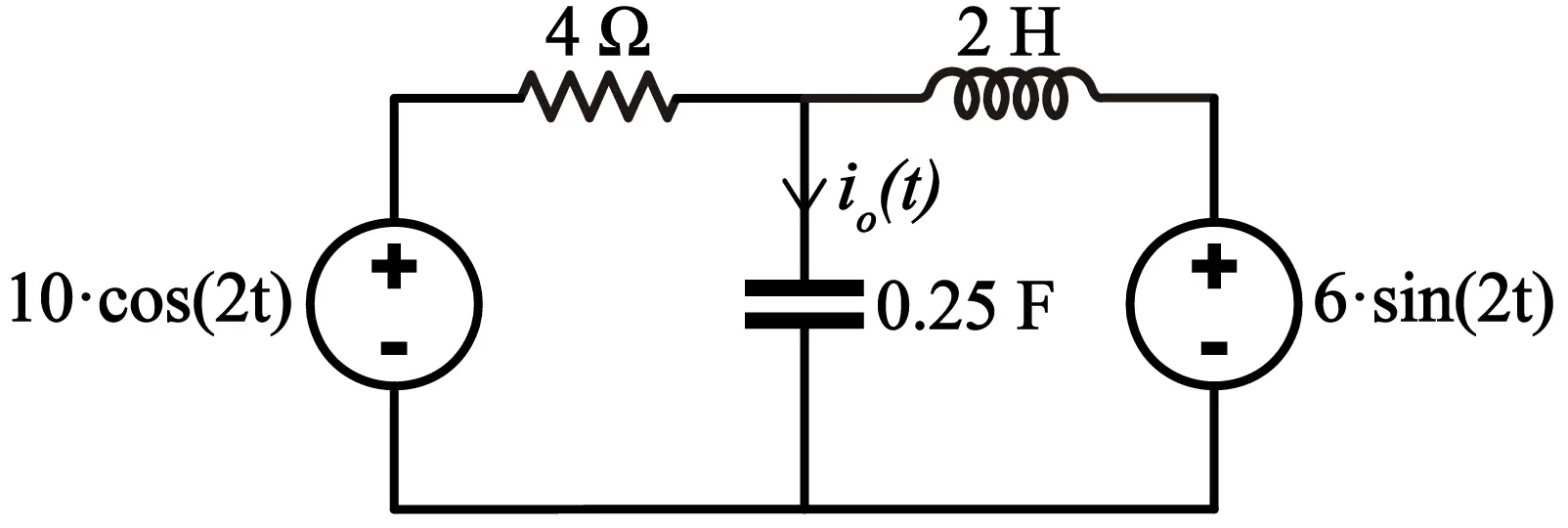
Un circuito sencillo, con dos fuentes de poder, en el que tenemos que encontrar la corriente io(t). A continuación, voy a describir los pasos que según mi criterio se deben seguir para analizar este circuito.
El primer paso para mí es convertir las impedancias y las fuentes de poder al dominio de la frecuencia. Para convertir las impedancias utilizamos la tabla de la sección anterior. A las fuentes de poder no les aplicamos Transformada de Laplace, sino que las convertimos al dominio de la frecuencia de la siguiente manera:
Nótese que en el dominio del tiempo utilizamos la v (minúscula) y en el dominio de la frecuencia usamos V (mayúscula). La razón para mantener las fuentes de poder como variables la explicaré más adelante. Dicho esto, nuestro circuito convertido al dominio de la frecuencia nos quedaría así: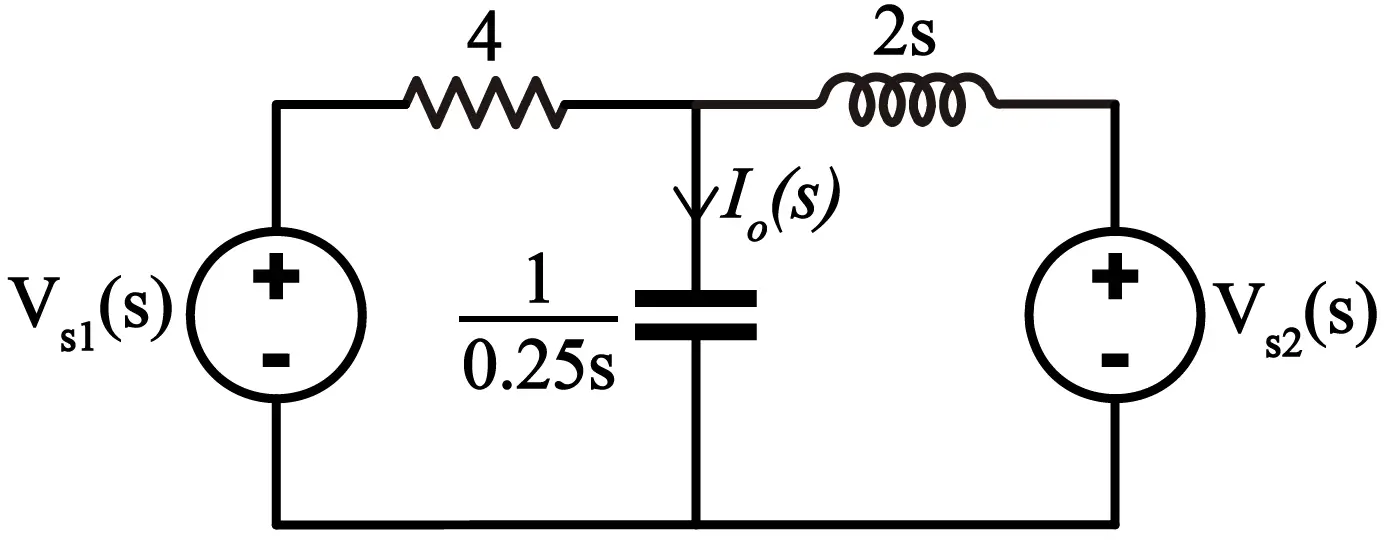
La resistencia permanece como 4. La inductancia pasa a ser una impedancia representada por 2s y el capacitor pasa a ser una impedancia representada por 1/0.25s. Esta transformación se ha hecho conforme a lo mostrado en la tabla de la sección anterior. Las fuentes de poder quedan expresadas como variables en el dominio de la frecuencia.
Una vez se convierte el circuito al dominio de la frecuencia se procede a utilizarlas técnicas de análisis de circuitos, ya sea análisis por mallas, análisis por nodos o cualquier otro método de análisis basado en la Ley de Ohm. En mi caso utilizaré el análisis de nodos para construir el siguiente sistema de ecuaciones:
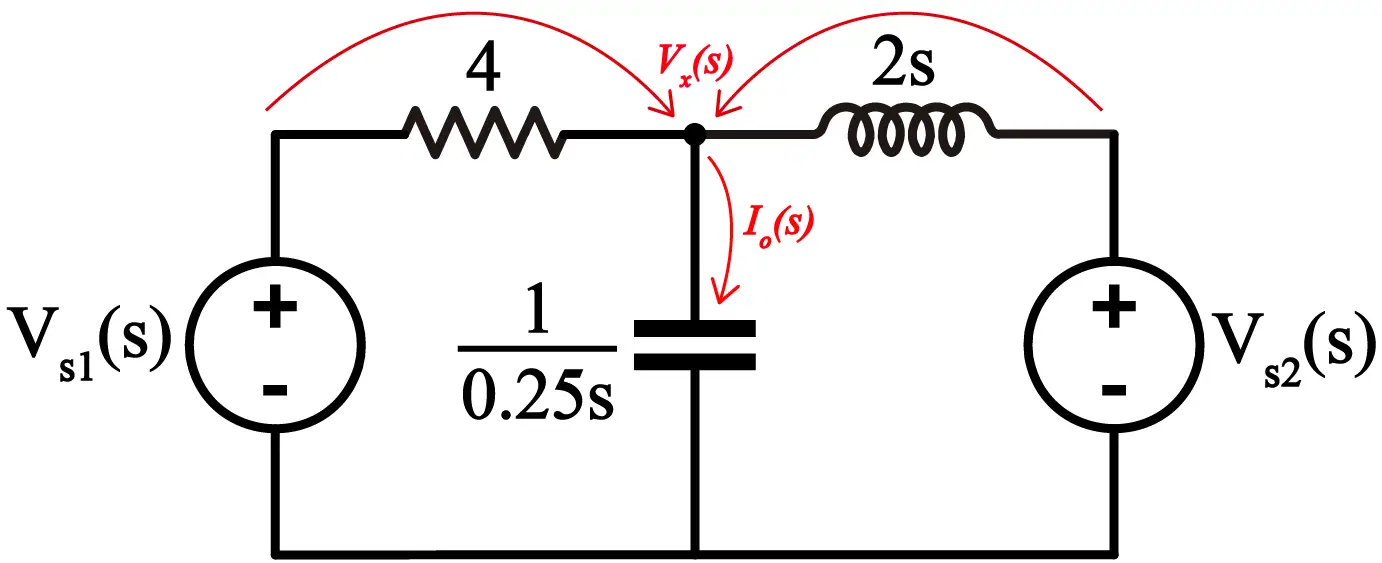
Sumaremos las dos corrientes que entran al nodo que he nombrado como Vx(s) y la igualaremos a la corriente Io(s). Luego definiremos la corriente Io(s) como el voltaje Vx(s) dividido por la impedancia del capacitor.
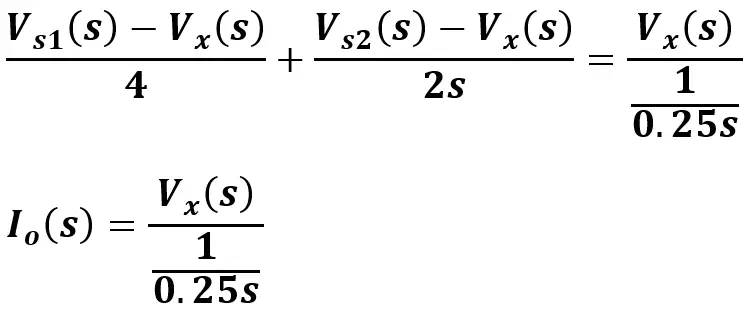
Estas ecuaciones han sido definidas con base en la Ley de Ohm y la Ley de Corrientes de Kirchhoff.
Este sistema de ecuaciones cuenta con dos incógnitas: Io(s) y Vx(s). Utilizando la calculadora voy a despejar el sistema de ecuaciones:
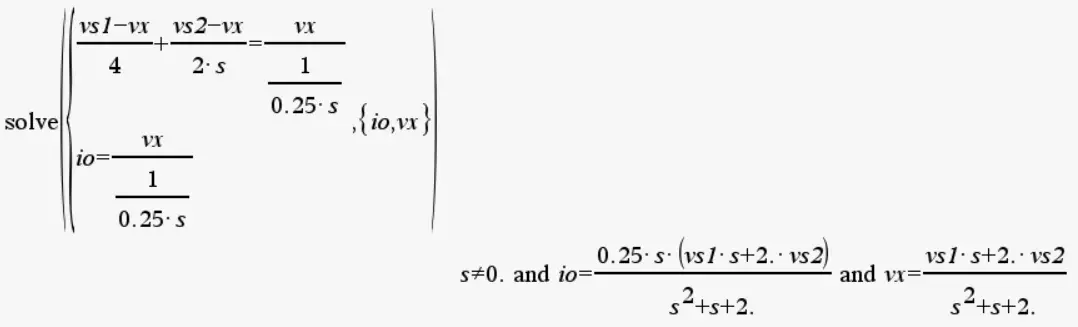
De esta forma, la expresión para Io(s) en el dominio de la frecuencia es:
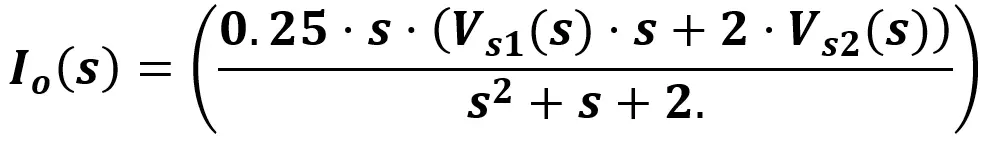
Para resolver el problema necesitamos la expresión para io(t). Hasta este punto tenemos Io(s). En este punto es donde nos toca tomar la decisión sobre el tipo de procedimiento que utilizaremos para expresar la respuesta, ya sea la Transformada Inversa de Laplace o el método de Frecuencia Compleja.
He aquí la importancia de dejar las fuentes expresadas como Vs1(s) y Vs2(s) pues, como veremos a continuación, podremos utilizar los dos métodos que estamos discutiendo para encontrar la respuesta al problema sin tener que recalcular todo desde el principio.
Transformada Inversa de Laplace
Para aplicar la Transformada Inversa de Laplace hace falta asignarle un valor a las fuentes de poder Vs1(s) y Vs2(s) utilizando la Transformada de Laplace de Vs1(t) y Vs2(t).
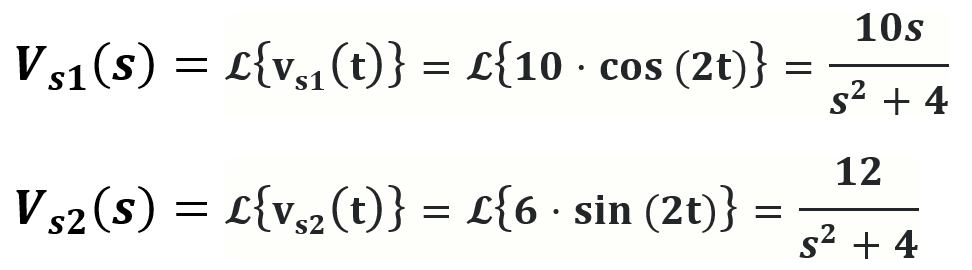
Estas operaciones las podemos hacer con la calculadora Ti-Nspire CX CAS:
Ahora remplazamos estas expresiones en la expresión Io(s) que definimos en la sección anterior:
Este polinomio lo podemos separar en varios polinomios más pequeños a través del método de fracciones parciales. Eso debe permitir que se formen polinomios que pueden ser convertidos al dominio de la frecuencia a través una tabla de Transformadas Inversas de Laplace:
Para mi no es necesario hacer este paso, pues cuento con la calculadora que me permite hacer Transformada Inversa de Laplace directamente:
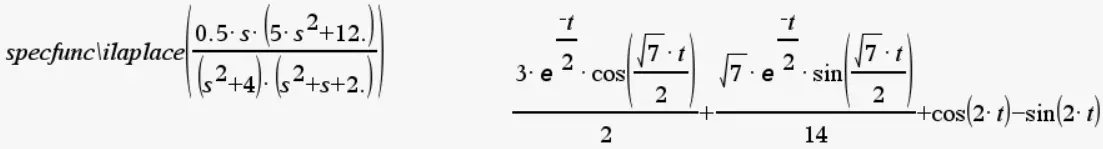
Esta sería la expresión final para io(t), la cual presento reajustada a continuación: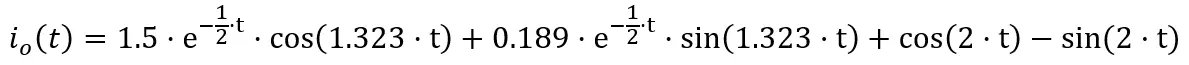
Esta vendría siendo la respuesta al problema. Este modelo matemático describe la corriente io(t) en cualquier tiempo mayor a t=0.
Debo destacar que la respuesta obtenida con la Transformada de Laplace es una respuesta exacta. Como explicaré más adelante, con el método de Frecuencia Compleja obtendremos una respuesta aproximada que convergerá con la respuesta de la Transformada de Laplace luego de que se extingan los términos con funciones exponenciales.
Frecuencia Compleja
El método de Frecuencia Compleja permite obtener una respuesta aproximada a un problema de análisis de circuitos en corriente alterna, sin tener que usar la Transformada Inversa de Laplace.
Este método es el que normalmente se utiliza en Análisis Senoidal en Estado Estable o análisis con fasores. También es la base para el análisis de circuitos eléctricos de potencia. Para poder aplicar este método hace falta entender el concepto de la variable de frecuencia compleja.
Aquí no hará falta hacer una Transformada Inversa de Laplace. Simplemente remplazaremos la variable «s» en el polinomio Io(s) por un número complejo, cuyo valor dependerá de la frecuencia angular (σ) y la frecuencia angular (ω) de la función excitatriz utilizada para alimentar el circuito eléctrico.
La siguiente tabla presenta la forma que tendrá la variable de frecuencia compleja en función de la(s) frecuencia(s) de la función excitatriz:
Al principio de este post invertimos una sección en explicar las características de esta función.
Analizando el circuito original, podemos identificar el tipo de función excitatriz de las fuentes de poder:
Ambas son fuentes de poder cosenoidales. Aún cuando la fuente de poder de la derecha utiliza la función seno, esta puede convertirse en una función coseno con un desfase de 90º. Las dos fuentes tienen la misma frecuencia angular: 2 rad/s (el número dentro del paréntesis que acompaña la «t»).
Tomando en cuenta esto podemos definir nuestra variable de frecuencia compleja:
En esta expresión, la «j» representa el operador imaginario, es decir, raíz cuadrada de -1:
Para los matemáticos el operador imaginario normalmente se representa con la letra «i», pero en Ingeniería Eléctrica se acostumbra utilizar «j» para evitar confusión con la i utilizada para representar la intensidad de corriente eléctrica.
Decimos que la «s» es la variable de frecuencia compleja porque dependiendo del tipo de función excitatriz esta variable puede ser un número real (fuente exponencial), imaginario (fuente senoidal), complejo (senoidal amortiguada) o cero (caso DC).
Nótese que para poder utilizar este método hace falta que todas las fuentes de poder utilicen la misma frecuencia angular y frecuencia neperiana. Si tuviésemos fuentes de poder con distintas frecuencias haría falta utilizar el método de superposición, el cual requiere de consideraciones especiales para su implementación. Esta es una desventaja de este médoto con respecto al de la Transformada de Laplace, el cual es independiente de la frecuencia de la o las funciones excitatrices.
Otro requerimiento de este método es definir las fuentes de poder en su forma fasorial. Esto lo podemos apreciar en la tabla que compartimos más arriba con los tipos de fuentes, específicamente en la columna de la derecha. Necesitamos definir las fuentes de poder VS1 y VS2 como fasores:
Básicamente lo que hacemos es tomar la amplitud y expresarla como un número complejo en su forma polar, cuyo ángulo de desfase será el desfase φ de la función coseno. Cuando tenemos una función seno la convertimos en coseno al agregarle un desfase de 90º, lo cual hace que la forma fasorial tenga un atraso de 90º.
Una vez se ha definido las fuentes de poder en su forma fasorial y se le ha asignado un valor a la variable de frecuencia compleja, remplazamos estos valores en la expresión Io(s) que dejamos definida hace un rato:
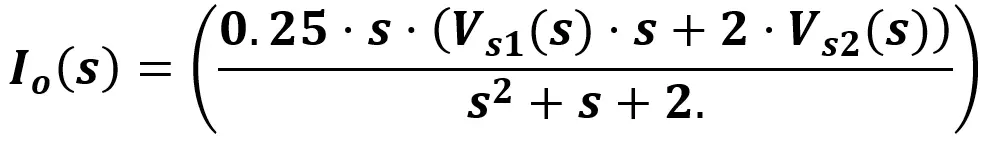
Al hacer el remplazo obtenemos lo siguiente:
La respuesta que hemos obtenido es:
Aquí tenemos la respuesta expresada en su forma rectangular y en su forma polar. A partir de este resultado podemos obtener una respuesta en el dominio del tiempo:
Las dos respuestas son válidas, una a partir de la respuesta rectangular y la otra a partir de la respuesta polar. Ambas son equivalentes, pero con notaciones distintas.
Si tu me preguntas a mi, yo prefieron la primera respuesta, la respuesta rectangular, para evitar el uso de ángulos de desfase con la respuesta polar. El uso de los ángulos de desfase siempre causa inconvenientes a la hora de introducir los datos a la calculadora.
Comparación de las respuestas obtenidas con cada método
La respuesta obtenida con la Transformada Inversa de Laplace fue:
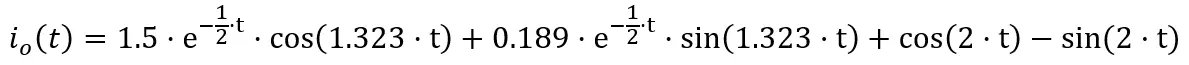
La respuesta obtenida con el método de Frecuencia Compleja fue:
En un principio parece que las respuestas no son iguales, pero en realidad son la misma respuesta. Como ya mencioné antes, la Transformada Inversa de Laplace permite calcular la respuesta exacta del problema. Esta respuesta está formada por la respuesta natural y la respuesta forzada, que a su vez es la respuesta senoidal en estado estable.
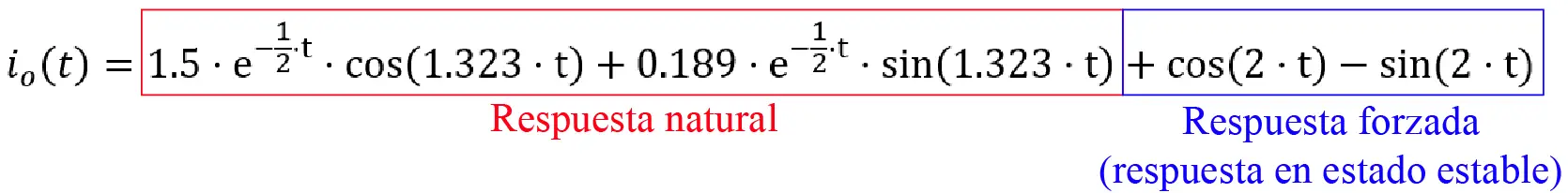
En el caso del método de fasores (Frecuencia Compleja), el resultado será la respuesta forzada, sin la respuesta natural.
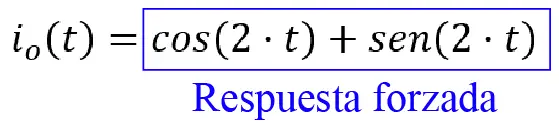
La respuesta natural se produce durante la energización del circuito, pero ésta se extinguirá luego de cierto tiempo. Esto se debe a que la respuesta natural está multiplicada por una función exponencial con exponente negativo. Este tipo de funciones cumplen con la forma:
En este tipo de funciones tenemos una constante de tiempo, denotada por τ, la cual permite calcular el tiempo de descarga de la función. En una función de este tipo el tiempo de descarga es igual a 5τ. Veamos un ejemplo:
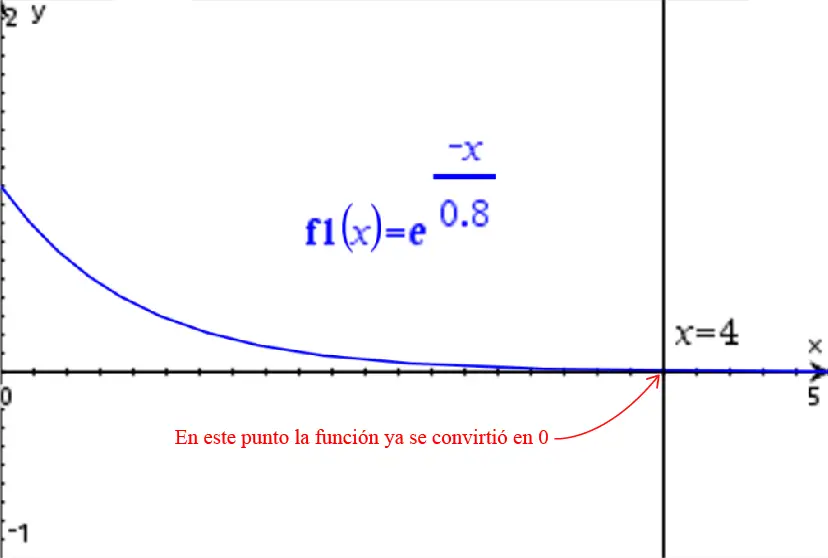
En este gráfico el valor de τ es 0.8. El tiempo de descarga de esta función será 5×0.8=4.0. Eso es precisamente lo que muestra la gráfica.
Dicho esto, cuando factorizamos la respuesta obtenida con la Transformada Inversa de Laplace tenemos:
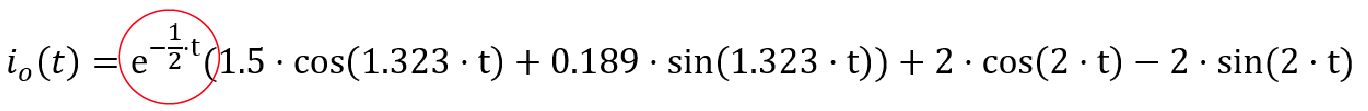
El término encerrado en rojo es una función exponencial con exponente negativo, tal como la que mostramos anteriormente. El tau es 2 (τ=2), por lo cual se espera que la respuesta natural se extinga luego de 10 segundos (5τ=10). Luego de este tiempo, la respuesta obtenida con el método de Frecuencia Compleja y la respuesta obtenida con la Transformada Inversa de Laplace convergerán en un mismo valor:
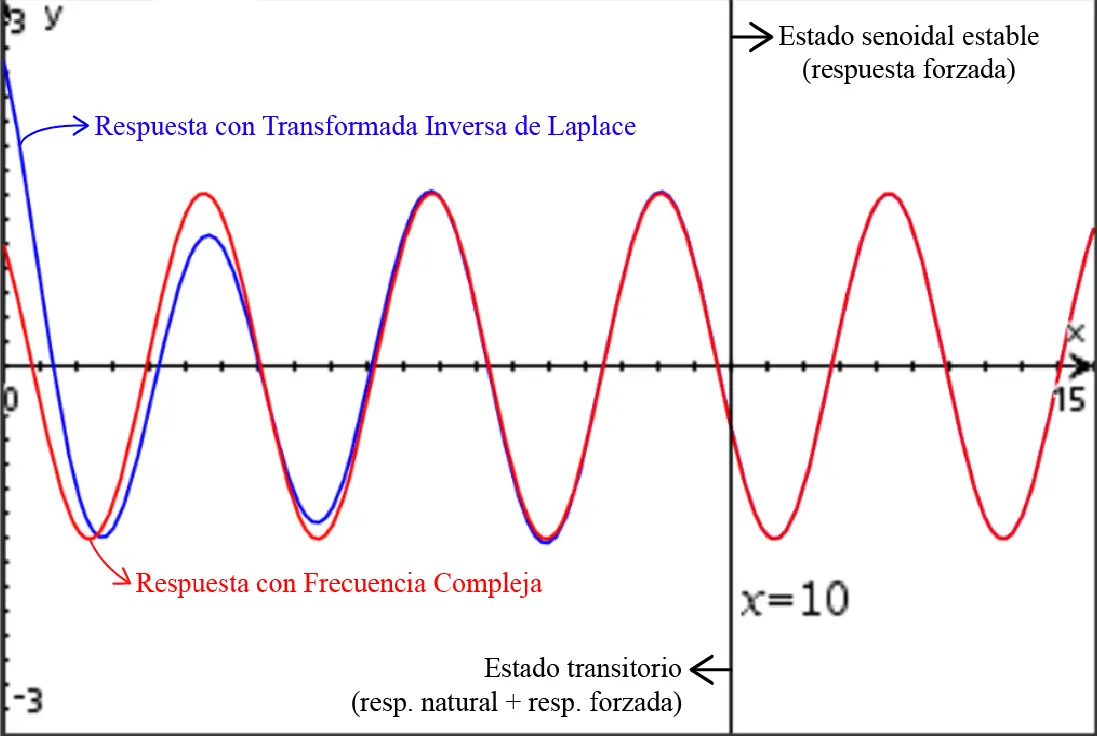
Como vemos, en los instantes iniciales de la energización del circuito se manifiesta la respuesta natural que calculamos con la Transformada Inversa de Laplace. Pero luego que se supera el tiempo 5τ de la función exponencial de la respuesta natural, las respuestas obtenidas con cada método de análisis convergen en una sola. Esta es la razón por la que se considera el método de Frecuencia Compleja como un método de análisi válido, pues aunque no nos permite calcular la respuesta natural del circuito, sí nos permite conocer la respuesta en estado estable.
Ventajas y desventajas de los métodos utilizados
El método de Frecuencia Compleja nos permite obtener la respuesta de estado estable de un circuito en corriente alterna sin tener que lidiar con la Transformada Inversa de Laplace. Dicho método requiere de un manejo algebraico importante, lo cual resulta impráctico cuando no se cuenta con las herramientas necesarias para resolver el problema matemático. Al representar las fuentes de poder como fasores y remplazar la variable de frecuencia compleja por el número complejo correspondiente no hace falta resolver una sola operación algebraica.
Por otro lado, cuando se trabaja con Frecuencia Compleja no es posible considerar fuentes de poder con múltiples frecuencias y se hace necesario utilizar el método de superposición. Esto hace que sea especialmente complicado utilizar esta técnica cuando se trabaja con sistemas con contenido armónico o componentes DC, tal como en los sistemas eléctricos actuales. Lo mismo aplica a circuitos eléctricos en los que la fuente de poder debe ser modelada por medio de una Serie de Fourier. Aún así, el método de Frecuencia Compleja o Análisis Senoidal en Estado Estable (Fasores) es el método preferido para el análisis de sistemas de potencia a nivel mundial.
La Transormada de Laplace se utiliza en casos donde sea imperativo conocer la respuesta natural de un sistema, en instancias en las que existan fuentes de poder con múltiples frecuencias o en sistemas con perturbaciones no periodicas. Recordemos que el método de Frecuencia Compleja nos da la respuesta estable a largo plazo e ignorando los instantes iniciales luego de un cambio en la función excitatriz del sistema.
Finalmente debo resaltar que en este post hemos analizado sistemas que energizados a partir de un estado energético nulo, es decir, sin energía almacenada en los inductores y capacitores. Cuando tenemos una carga inicial en inductores y capacitores el método de Frecuencia Compleja se vuelve especialmente difícil de utilizar por todo el procedimiento matemático que se requiere para el cálculo de la respuesta natural. Pero ese es un tema que trataré en otro post más adelante.
Conclusión
En este post he presentado una explicación detallada sobre el análisis de circuitos eléctricos con fuentes de poder dependientes del tiempo (y/o corriente alterna). Se han mencionado dos métodos principales: la Transformada de Laplace y la Frecuencia Compleja. Se ha presentado un ejemplo de cómo utilizar estos métodos para analizar un circuito y obtener la respuesta del circuito en el dominio del tiempo. También se ha mencionado la función excitatriz como un modelo matemático que permite describir cualquier tipo de fuente de poder en un circuito eléctrico.
Espero que este post haya sido de ayuda para entender cómo se realiza el análisis de circuitos con fuentes de poder dependientes del tiempo. Si tienes alguna pregunta o comentario, ¡estaré encantado de responder! ¡Gracias por leer!
