En este post, vamos a revisar el modelado matemático del algoritmo k-Nearest Neighbors (kNN). Esta técnica, ampliamente adoptada en el aprendizaje automático, opera bajo la premisa de que puntos de datos similares en el espacio de características suelen compartir etiquetas afines.
El algoritmo kNN se encarga de clasificar un nuevo punto de datos observando las etiquetas de sus vecinos más cercanos en el conjunto de entrenamiento, determinando esta proximidad mediante medidas de distancia como la euclidiana. A pesar de su aparente sencillez conceptual, sumergirse en el modelado matemático de kNN nos proporciona insights profundos sobre su funcionamiento y sienta las bases para explorar optimizaciones y variantes del mismo.
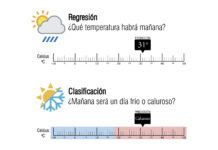
¿Regresión o Clasificación? La Dualidad del kNN
Antes de sumergirnos en los detalles matemáticos del algoritmo k-Nearest Neighbors (kNN), es crucial reconocer que este algoritmo posee dos aplicaciones principales: regresión y clasificación. Aunque ambas versiones operan bajo el mismo principio de considerar los «vecinos más cercanos», difieren significativamente en cómo interpretan y utilizan esta información.
Sobre las diferencias entre regresión y clasificación ya escribimos un post aquí en Panama Hitek: ¿Cuál es la diferencia entre regresión y clasificación en Machine Learning?.
En este artículo, nos adentraremos en el modelado matemático de ambas variantes del algoritmo kNN: regresión y clasificación. Comenzaremos explorando la regresión para luego pasar a la clasificación, ya que los procedimientos matemáticos empleados en cada caso varían significativamente.
Modelado matemático del regresor KNN
Definición del dataset
Cuando trabajamos con KNN como algoritmo de regresión, es esencial partir de un dataset estructurado adecuadamente. En general, el proceso de aprendizaje automático implica dividir nuestro dataset en dos partes principales: el dataset de entrenamiento y el de pruebas. Estos datasets nos permiten entrenar el modelo y luego evaluar su rendimiento en datos no vistos previamente.
Matemáticamente los datasets se definen de la siguiente manera:
$$\mathcal{D} = \{ (\mathbf{x}_1, y_1), (\mathbf{x}_2, y_2), \dots, (\mathbf{x}_n, y_n) \}$$
Donde:
- \(\mathbf{x}_i\) representa un vector de características en \( \mathbb{R}^d \).
- \(y_i\) es el valor o etiqueta correspondiente, que puede ser un valor continuo (en regresión) o una etiqueta categórica (en clasificación).
- \(n\) es el número de ejemplos en el dataset de entrenamiento.
Observa la distinción notacional entre \(\mathbf{x}_i\) y \(y_i\): \(\mathbf{x}_i\) es un vector, mientras que \(y_i\) es un valor escalar. La razón detrás de esta designación es que un conjunto de datos puede contener múltiples características asociadas a un único valor de \(y_i\).
El vector de features (o características) luce así:
$$\mathbf{x}_i = [x_{i_1}, x_{i_2}, \ldots, x_{i_d}]$$
Donde:
- \(\mathbf{x}_i\) es el vector de características para el i-ésimo punto de datos.
- \(x_{i_1}, x_{i_2}, \ldots, x_{i_d}\) son las componentes individuales del vector de características, donde \(d\) representa la dimensión del espacio de características.
En esta notación, \(\mathbf{x}_i\) es un vector que contiene \(d\) componentes, cada una de las cuales representa una característica específica del punto de datos \(i\). Estas características pueden ser valores numéricos, categóricos o cualquier tipo de información relevante para el problema de aprendizaje automático en cuestión.

En la imagen anterior tomamos como ejemplo el Red Wine Dataset, del que ya hemos escrito en este blog, para representar gráficamente el vector de características \(\mathbf{x}_i\) y el valor o etiqueta correspondiente \(y_i\).
Selección de la Métrica de Distancia
Uno de los aspectos fundamentales del algoritmo kNN en regresión es la elección de la métrica de distancia que se utilizará para medir la similitud entre los puntos de datos. La métrica de distancia determina cómo calculamos la distancia entre el nuevo punto de datos que queremos predecir y los puntos de datos existentes en el conjunto de entrenamiento.
La medida de distancia más comúnmente utilizada en kNN es la distancia euclidiana. La distancia euclidiana entre dos puntos \( \mathbf{x}_i \) y \( \mathbf{x}_j \) en un espacio de características de \(d\) dimensiones se calcula de la siguiente manera:
$$
\text{Distancia Euclidiana}(\mathbf{x}_i, \mathbf{x}_j) = \sqrt{\sum_{l=1}^{d} (x_{i_l} – x_{j_l})^2}
$$
En esta fórmula, \(x_{i_k}\) y \(x_{j_k}\) representan las componentes individuales de los vectores de características \( \mathbf{x}_i \) y \( \mathbf{x}_j \), respectivamente. La raíz cuadrada se aplica a la suma de los cuadrados de las diferencias entre las componentes para calcular la distancia total.
Si tomamos como ejemplo dos muestras consecutivas del Red Wine Quality Dataset:

Los features de esas dos muestras se definen como dos vectores:
\[
\mathbf{x}_1 = \begin{bmatrix}
7.4 & 0.7 & 0.0 & 1.9 & 0.076 & 11.0 & 34.0 & 0.9978 & 3.51 & 0.56 & 9.4
\end{bmatrix}
\]
\[
\mathbf{x}_2 = \begin{bmatrix}
7.8 & 0.88 & 0.0 & 2.6 & 0.098 & 25.0 & 67.0 & 0.9968 & 3.2 & 0.68 & 9.8
\end{bmatrix}
\]
El simbolo de la sumatoria dentro de la raiz cuadrada nos indica que tenemos que restar todos los valores de los vectores \( \mathbf{x}_1 \) y \( \mathbf{x}_2 \) y elevarlos al cuadrado. Lo hacemos de la siguiente manera:
\( (x_{1_1} – x_{2_1})^2 = (7.4 – 7.8)^2 = 0.16 \)
\( (x_{1_2} – x_{2_2})^2 = (0.7 – 0.88)^2 = 0.0324 \)
\( (x_{1_3} – x_{2_3})^2 = (0.0 – 0.0)^2 = 0 \)
\( (x_{1_4} – x_{2_4})^2 = (1.9 – 2.6)^2 = 0.49 \)
\( (x_{1_5} – x_{2_5})^2 = (0.076 – 0.098)^2 = 0.000484 \)
\( (x_{1_6} – x_{2_6})^2 = (11.0 – 25.0)^2 = 196 \)
\( (x_{1_7} – x_{2_7})^2 = (34.0 – 67.0)^2 = 1089 \)
\( (x_{1_8} – x_{2_8})^2 = (0.9978 – 0.9968)^2 = 0.000001 \)
\( (x_{1_9} – x_{2_9})^2 = (3.51 – 3.2)^2 = 0.0961 \)
\( (x_{1_{10}} – x_{2_{10}})^2 = (0.56 – 0.68)^2 = 0.0144 \)
\( (x_{1_{11}} – x_{2_{11}})^2 = (9.4 – 9.8)^2 = 0.16 \)
Como estos elementos están dentro de una sumatoria, los sumamos todos. La distancia euclidiana se calcula como:
\[
\text{Distancia} = \sqrt{(x_{1_1} – x_{2_1})^2 + (x_{1_2} – x_{2_2})^2 + \ldots + (x_{1_{11}} – x_{2_{11}})^2}
\]
Reemplazando:
\[
\text{Distancia} = \sqrt{0.16 + 0.0324 + \ldots + 0.16}
\]
El resultado obtenido, \( \approx 35.86 \), representa la distancia euclidiana entre las dos muestras del conjunto de datos del vino tinto. Esta distancia cuantifica cuán diferentes o similares son estas dos muestras en términos de sus características. Cuanto menor sea esta distancia, más similares serán las dos muestras y viceversa.
Es importante destacar que, dependiendo del problema y los datos, otras métricas de distancia como la distancia de Manhattan o la distancia de Minkowski pueden ser más apropiadas. La elección de la métrica de distancia debe considerarse cuidadosamente y adaptarse al contexto del problema.
Sin embargo, calcular la distancia entre solo dos muestras es solo una pequeña parte del proceso general del algoritmo kNN. Para hacer una predicción o clasificación usando kNN, es necesario seguir algunos pasos adicionales, los cuales veremos a continuación.
Determinar el valor de «k»
El corazón del algoritmo k-Nearest Neighbors (kNN) reside en la elección del parámetro \( k \), que representa el número de vecinos que se considerarán al hacer predicciones. El valor de \( k \) no solo influye en la precisión del modelo, sino que también determina cómo el algoritmo responde a los datos de entrada.
El término «kNN» proviene de «K-Nearest Neighbors», que se traduce como «Los K vecinos más cercanos». En este contexto, «cercano» se refiere a la similitud o distancia entre puntos de datos en el espacio de características. Por lo tanto, el objetivo es identificar cuáles son los \( k \) puntos de datos más similares o cercanos a un nuevo punto de datos dado.
Por ejemplo, si optamos por un valor de \( k = 3 \), el algoritmo considerará las tres muestras más cercanas al punto de datos en cuestión. Estas tres muestras influirán directamente en la predicción o clasificación que se realice. Si la mayoría de estos tres vecinos pertenece a una categoría particular (en el caso de la clasificación) o tiene valores similares (en el caso de la regresión), es probable que el punto de datos en cuestión también pertenezca a esa categoría o tenga un valor similar.
La elección de \( k \) es crucial: un valor de \( k \) demasiado pequeño puede hacer que el modelo sea muy sensible al ruido o a las anomalías en los datos, mientras que un \( k \) demasiado grande puede hacer que el modelo sea demasiado general y no capte las sutilezas o patrones en los datos. Además, es importante tener en cuenta que a medida que \( k \) aumenta, la carga computacional del algoritmo también aumenta, ya que tiene que considerar más vecinos al tomar decisiones.
Por lo general, el valor óptimo de \( k \) se determina mediante técnicas como la validación cruzada, donde se prueba el rendimiento del modelo con diferentes valores de \( k \) y se elige el que ofrece el mejor equilibrio entre precisión y complejidad.
Predicción con el regresor KNN
Una vez que hemos determinado el valor óptimo de \( k \) y definido nuestra métrica de distancia, podemos utilizar el algoritmo kNN para hacer predicciones en datos no vistos anteriormente. El proceso de predicción en regresión kNN es:
- Para un nuevo punto de datos \( \mathbf{x}_{\text{new}} \), calcula su distancia a cada punto en el conjunto de entrenamiento usando la métrica de distancia seleccionada.
- Ordena estas distancias en orden ascendente y selecciona las \( k \) distancias más cortas (los \( k \) vecinos más cercanos).
- Para hacer una predicción de regresión, calcula el promedio de los valores \( y \) asociados a estos \( k \) vecinos más cercanos. Matemáticamente sería:
\[ \hat{y}_{\text{new}} = \frac{1}{k} \sum_{i \in \text{vecinos más cercanos}} y_i \]
Esta ecuación representa un concepto muy simple, un cálculo de un promedio. Se suman los valores de las \(y\) de los k-vecinos más cercanos y se divide entre el numero de vecinos más cercanos.
Resumen del algoritmo KNN de regresion
Después de haber analizado cada componente del algoritmo, estamos en posición de presentar el algoritmo para estimar un valor de regresión basado en un conjunto de datos previamente conocido:

A pesar de su simplicidad, el algoritmo kNN demuestra ser efectivo en numerosas ocasiones. Representa una opción ágil y sencilla para elaborar modelos de regresión que son rápidos y eficientes. Si bien no garantiza éxito en todos los escenarios, en muchos casos produce resultados satisfactorios.
Modelado matemático del clasificador KNN
Para el caso del clasificador kNN, el tratamiento del conjunto de datos y el cálculo de las distancias son idénticos a los del regresor kNN. La estructura del conjunto de datos, el vector de características y la métrica de distancia utilizada permanecen consistentes. Sin embargo, hay diferencias clave en cómo se utiliza esta información para hacer una predicción:
- Predicción basada en la moda: En lugar de calcular un promedio de los valores \( y \) de los vecinos más cercanos, en la clasificación se determina la moda (la etiqueta que aparece con más frecuencia) entre los \( k \) vecinos más cercanos. Esta etiqueta será la predicción para el nuevo punto de datos.
- Resultados discretos: Las predicciones en la clasificación son etiquetas discretas (categorías) en lugar de valores continuos.
- Probabilidad de pertenencia: Algunas variantes del clasificador kNN pueden proporcionar una probabilidad de pertenencia a cada clase. Por ejemplo, si \( k = 5 \) y tres de los vecinos más cercanos pertenecen a la clase A y dos a la clase B, se podría decir que hay un 60\% de probabilidad de que el punto pertenezca a la clase A y un 40\% de que pertenezca a la clase B.
El clasificador KNN es, al igual que el regresor, un modelo muy simple basado en un concepto sencillo: la cercanía con respecto a otras muestras. «Dime con quien andas y te diré quien eres», nunca mejor dicho.
Aquí en Panama Hitek ya escribimos un artículo en el que utilizamos KNN en la clasificación de imágenes de dígitos manuscritos. Los invito a que lo revisen para que vean como se configura y se utiliza en Python.
Resumen del algoritmo KNN de clasificación
Aquí tenemos el algoritmo KNN para clasificación:

Similar al algoritmo anterior, pero calculando la moda de las etiquetas más cercanas y utilizando dicho cálculo para estimar el resultado de la clasificación.
Optimización de Hiperparámetros en kNN
El ajuste de hiperparámetros es esencial para mejorar el rendimiento de un algoritmo. En el caso de kNN, hay varios hiperparámetros clave que pueden ser ajustados para adaptar el algoritmo a un conjunto de datos específico. A continuación, se destacan algunos de los hiperparámetros más importantes:
- Valor de k: Es el número de vecinos y es uno de los hiperparámetros más críticos del algoritmo. Un k pequeño puede hacer que el modelo sea susceptible al ruido, mientras que un k grande puede hacer que el modelo ignore las variaciones locales. Se recomienda usar validación cruzada para encontrar el valor óptimo de k.
- Métrica de Distancia: Aunque la distancia euclidiana es común, hay ocasiones en que otras métricas, como la distancia de Manhattan, pueden ser más adecuadas. La elección depende de la naturaleza y estructura de los datos. Las posibles opciones de métricas de distancia incluyen:
-
- Distancia Euclidiana (predeterminada)
- Distancia de Manhattan
- Distancia de Minkowski
- Distancia de Hamming
- Distancia de Jaccard
-
- Pesado de Vecinos: Se puede asignar un peso a los vecinos basado en su distancia al punto de interés. Los vecinos más cercanos pueden tener más influencia en la decisión que aquellos más lejanos. Usualmente, se utiliza un peso inversamente proporcional a la distancia.
- Estrategia de Almacenamiento: Para conjuntos de datos grandes, es necesario considerar cómo se almacenan los datos. Estructuras como KD-Tree o Ball Tree pueden ser útiles para acelerar las consultas de vecinos más cercanos en grandes conjuntos de datos.
- Algoritmo de Búsqueda de Vecinos: Dependiendo del tamaño y estructura del conjunto de datos, diferentes algoritmos para buscar los k vecinos más cercanos pueden ser más eficientes.
Ajustar estos hiperparámetros adecuadamente puede mejorar significativamente el rendimiento del modelo kNN en un conjunto de datos específico. La experimentación y validación son clave para encontrar la combinación óptima de hiperparámetros.
Conclusión
En este post hemos explorado en profundidad el modelado matemático del algoritmo k-Nearest Neighbors (kNN) en sus dos aplicaciones principales: regresión y clasificación.
En el caso de la regresión, hemos analizado cómo se estructura el conjunto de datos y cómo se calcula la distancia euclidiana entre puntos de datos. Además, hemos destacado la importancia de elegir el valor adecuado de «k» para lograr un equilibrio entre la precisión y la robustez del modelo de regresión kNN. Finalmente, hemos presentado el proceso de predicción en regresión, que se basa en el promedio de los valores de los k vecinos más cercanos.
Por otro lado, en la clasificación, hemos resaltado que, aunque los pasos iniciales son similares a los de la regresión, la predicción se basa en la moda de las etiquetas de los k vecinos más cercanos. También hemos mencionado la posibilidad de obtener probabilidades de pertenencia a cada clase en algunas variantes del clasificador kNN.
Además, hemos discutido la importancia de ajustar los hiperparámetros del algoritmo, como el valor de «k», la métrica de distancia, el peso de los vecinos y otros, para adaptar el modelo kNN a las características específicas del conjunto de datos.
En resumen, el algoritmo kNN, a pesar de su simplicidad conceptual, es una herramienta poderosa en el campo del aprendizaje automático y la minería de datos. Su capacidad para tomar decisiones basadas en la proximidad entre datos lo hace versátil y aplicable en una amplia gama de problemas, y su rendimiento puede mejorarse significativamente mediante la selección adecuada de hiperparámetros y técnicas de optimización.