Identificación y eliminación de outliers en Machine Learning

En el contexto de Machine Learning, los outliers (o valores atípicos) son observaciones que se desvían notablemente de las demás observaciones en un conjunto de datos. Estos puntos pueden surgir debido a variabilidades en las mediciones o errores en la recopilación de datos. En términos más simples, si imagináramos visualizar un conjunto de datos en un gráfico, los outliers serían aquellos puntos que están «fuera de lugar» o «lejos del grupo principal» de datos.

Por ejemplo, en mi post anterior, Red Wine Quality dataset: ¿Regresión o Clasificación?, exploramos un poco las características del Red Wine Quality Dataset. Utilizamos una transformación de coordenadas PCA en 3 dimensiones y obtuvimos el siguiente gráfico:

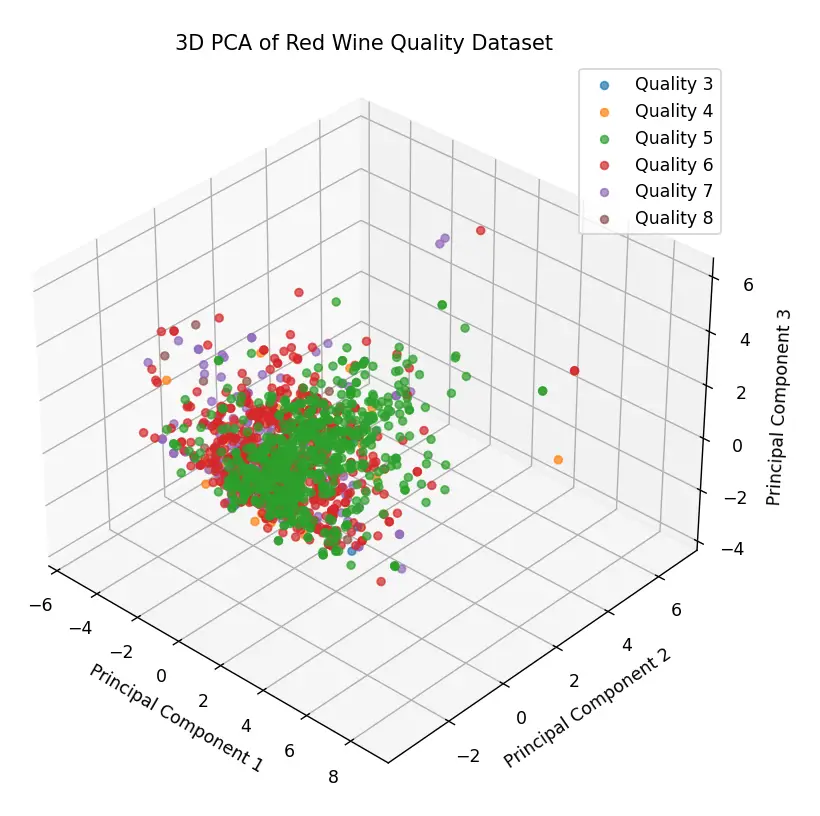Como vemos, el gráfico presenta un cúmulo de puntos concentrados alrededor de una coordenada, con algunos puntos dispersos alrededor de la nube de puntos. Esos serían los outliers de este dataset:

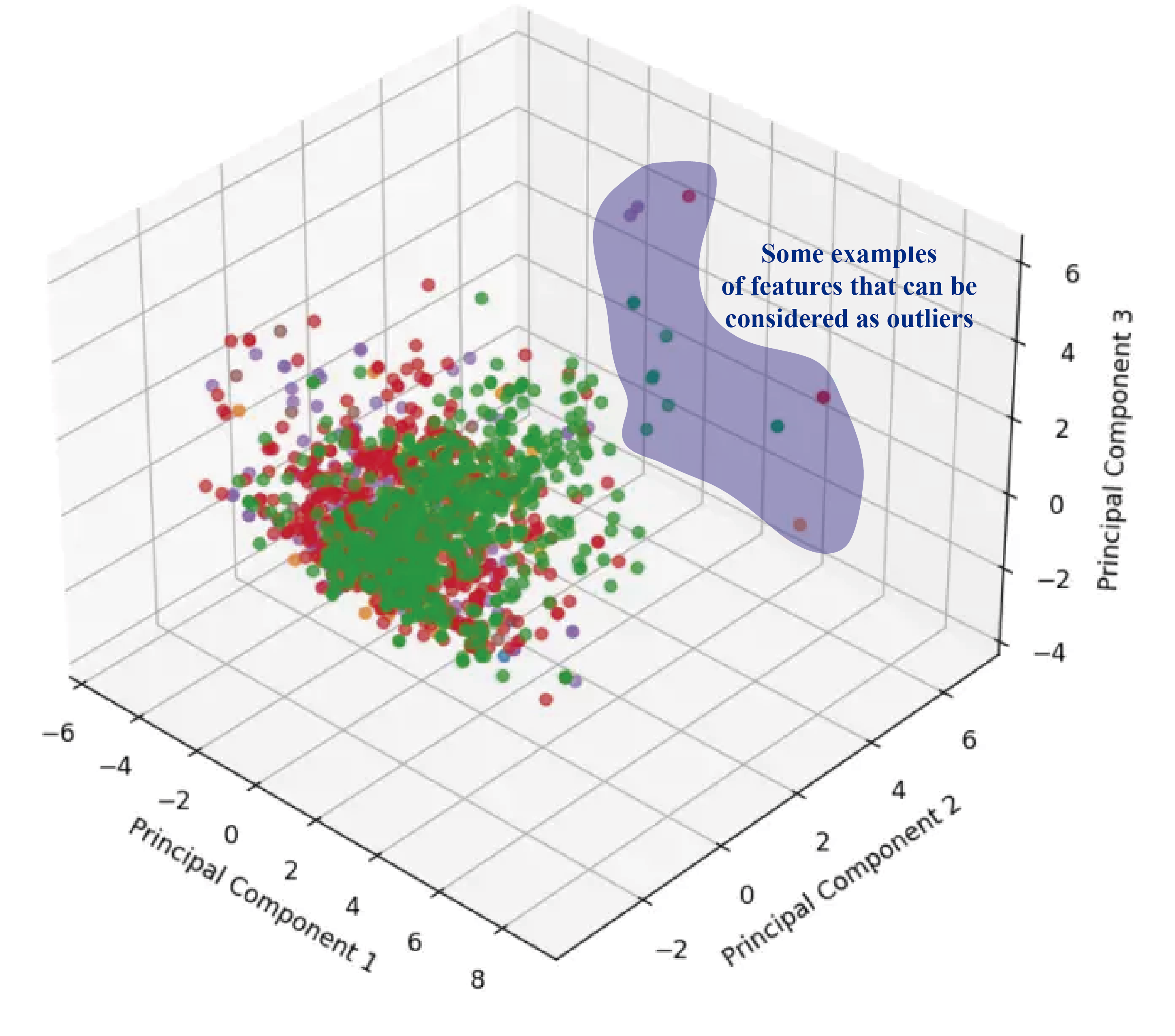
Los valores sombreados en azul son algunos ejemplos de outliers, aunque probablemente no son los únicos. En la imagen mostrada los estamos identificando de manera visual, pero existen técnicas que permiten identificar estos valores de manera analítica.

En este artículo, profundizaremos en las técnicas empleadas en Machine Learning y Ciencia de Datos para identificar y eliminar outliers. Analizaremos diversas estrategias y evaluaremos su impacto en los resultados de los algoritmos de regresión y clasificación que discutimos en nuestra publicación previa.

Sin más que decir, empezemos.

¿Qúe son los outliers?

En el contexto de Ciencia de Datos, un outlier es una observación (o muestreo) que se desvía significativamente y parece alejada del patrón general de una muestra. Es un término frecuentemente utilizado por analistas y científicos de datos, ya que si no se le presta la debida atención, puede llevar a estimaciones erróneamente y/o imprecisas.

Las razones por las cuales se producen los outliers pueden ser variadas:

• Errores de Ingreso de Datos: Los errores humanos, ya sea durante la recopilación, registro o ingreso de datos, pueden generar outliers. Un simple error tipográfico o una mala interpretación al ingresar datos puede resultar en valores que se desvíen significativamente del patrón general.
• Errores de Medición: Esta es una fuente común de outliers. Ocurre cuando el instrumento utilizado para la medición resulta ser defectuoso. Un calibrado inadecuado o fallos en los instrumentos de medición pueden llevar a registros que no reflejen la realidad.
• Outliers Naturales: No todos los outliers son producto de errores. En algunos casos, una observación puede ser genuinamente diferente del resto. Estos outliers, llamados naturales, reflejan eventos raros, anomalías o simplemente variaciones naturales en una población. Por ejemplo, en un conjunto de datos de estaturas, una persona extremadamente alta o baja podría ser un outlier natural.

Además de las razones detrás de la presencia de outliers, es importante mencionar que pueden clasificarse en dos tipos: Univariados y Multivariados.

• Outliers Univariados: Son aquellos que se pueden identificar al analizar la distribución de una sola variable. El ejemplo previamente discutido sobre la estatura es un caso de outlier univariado.
• Outliers Multivariados: Son outliers en un espacio n-dimensional. Se encuentran al considerar combinaciones de valores de diferentes variables. Por ejemplo, al combinar edad y salario, podríamos identificar personas que, aunque no son outliers en ninguna de las variables por separado, sí lo son cuando se consideran conjuntamente.

Es crucial para los científicos y analistas de datos identificar y, si es necesario, tratar estos outliers, ya que su presencia puede sesgar el análisis y llevar a conclusiones erróneas.

¿Cómo se identifican los outliers?

1. Visualización de Datos
   • Boxplots (Diagramas de caja): Los boxplots visualizan la variabilidad y detectan valores que caen fuera de los «bigotes» y que podrían ser considerados outliers.
   • Histogramas: Permiten ver la distribución de datos y observar valores atípicos.
   • Scatter plots (Gráficos de dispersión): Útiles para identificar outliers en datasets multivariados.
2. Pruebas de Hipótesis (Hypothesis Testing): Utilizadas para determinar si un punto de datos es significativamente diferente del resto de la muestra.
3. Método Z-Score: Mide cuántas desviaciones estándar está un punto de datos del promedio. Un Z-Score muy alto o muy bajo puede indicar un outlier.
4. Z-Score Robusto (Robust Z-score): Una adaptación del Z-score que es menos sensible a outliers.
5. Método I.Q.R (I.Q.R method): Se basa en la diferencia entre el tercer y primer cuartil. Datos que caen fuera de 1.5 veces el IQR por encima del tercer cuartil o por debajo del primer cuartil pueden ser considerados outliers.
6. Método de Winsorización (Winsorization method/Percentile Capping): Limita los valores extremos a un cierto percentil, reduciendo el impacto de los outliers sin eliminarlos.
7. Métodos de Clustering
   • K-Means: Aunque es principalmente un algoritmo de clustering, puede usarse para detectar outliers al observar puntos de datos que están lejos de los centroides de los clústeres.
   • DBSCAN: Método de clustering basado en densidad que puede identificar puntos en regiones de baja densidad y considerarlos como outliers.
8. Isolation Forest: Diseñado específicamente para la detección de outliers, se basa en la idea de que los outliers son más fáciles de «aislar» que los puntos normales.
9. Métodos de Profundidad
   • Envoltura convexa: Identifica outliers observando puntos de datos que no están en la envoltura convexa de un conjunto de datos.
10. Métodos Basados en Redes Neuronales
    • Autoencoders: Son una subclase de redes neuronales que se entrenan para reconstruir sus entradas. Los puntos de datos que el autoencoder reconstruye mal pueden ser considerados outliers.
11. Métodos Basados en Distancia:
    • K-Nearest Neighbors (K-NN): Los puntos de datos cuya distancia a sus k vecinos más cercanos supera un cierto umbral pueden ser considerados outliers.
12. Métodos de Regresión:
    • Modelos lineales: Observar los residuos de un modelo lineal puede ayudar a identificar outliers.

En esta publicación, nos centraremos en los métodos más utilizados para identificar outliers, dado que abordar todos sería extenso. Sin embargo, planeo explorar en detalle cada uno de los métodos mencionados en futuras publicaciones, las cuales estarán vinculadas a esta entrada.

Identificación de outliers por medio de visualización de datos

Como ya mencionamos al principio de este post, es posible identificar outliers en el Red Wine Quality Dataset con solo observar la representación tridimensional de la transformación PCA.

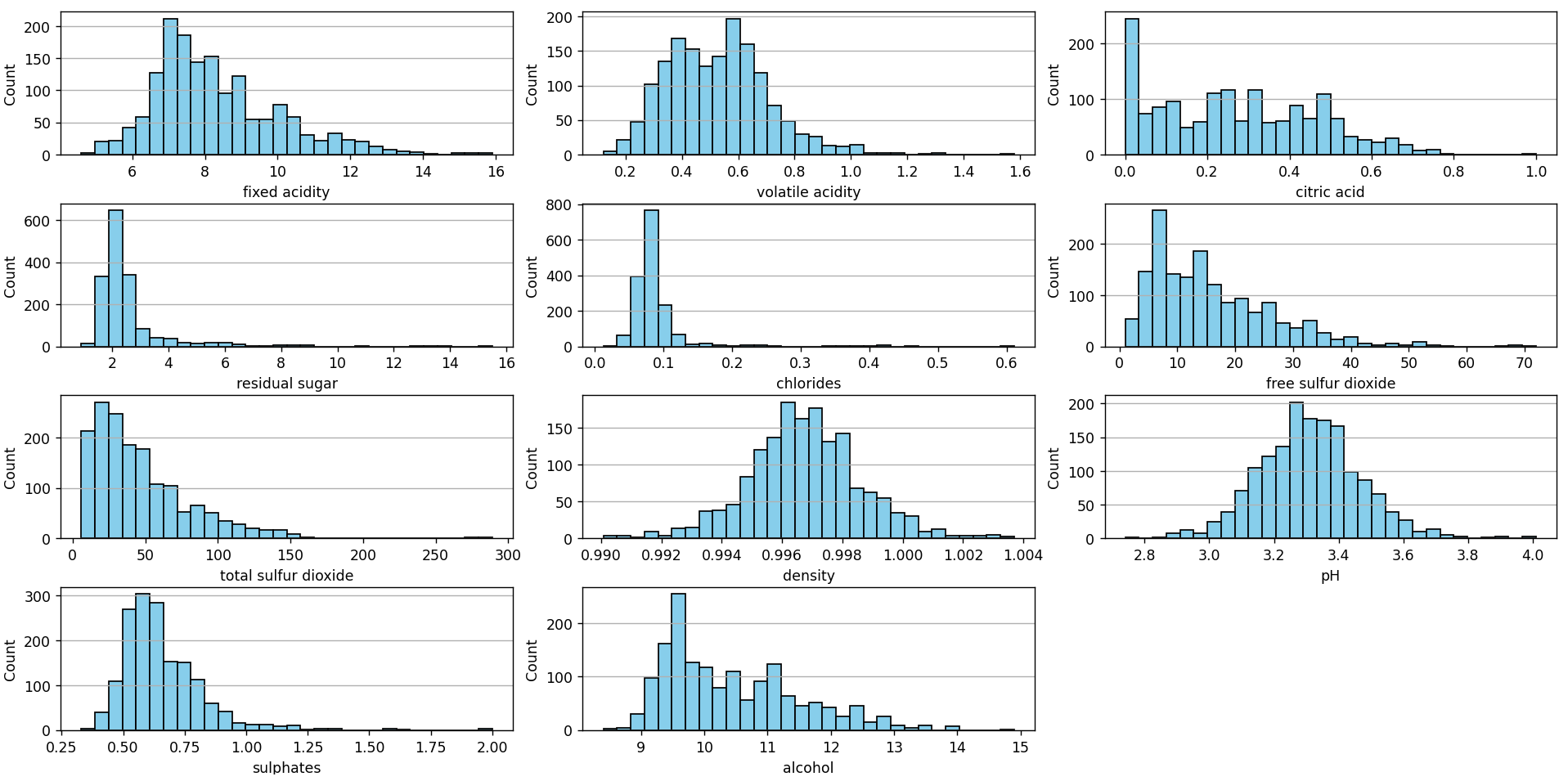
En mi post de Red Wine Quality dataset: ¿Regresión o Clasificación? también presentamos los histogramas de cada una de las características (features) del dataset:

Este gráfico puede construirse utilizando el siguiente script en Python, disponible en nuestro repositorio en Github. Visualmente se logran identificar varios valores que pueden ser considerados como outliers:

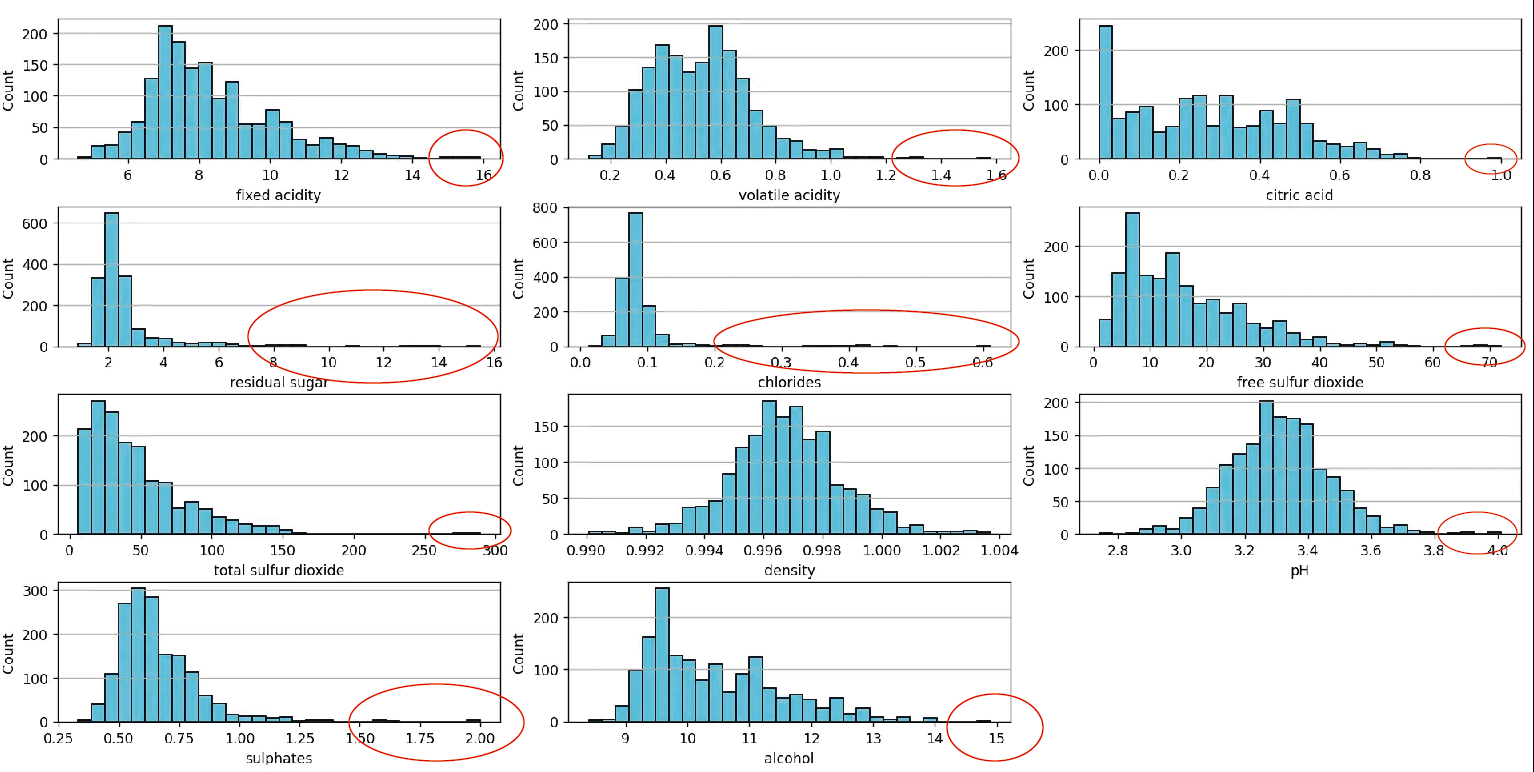
Estos valores claramente se separan del resto de los datos, lo cual los convierte en outliers. Otra forma de visualizarlos es con un scatter plot, la cual podrán ver en la siguiente imagen:

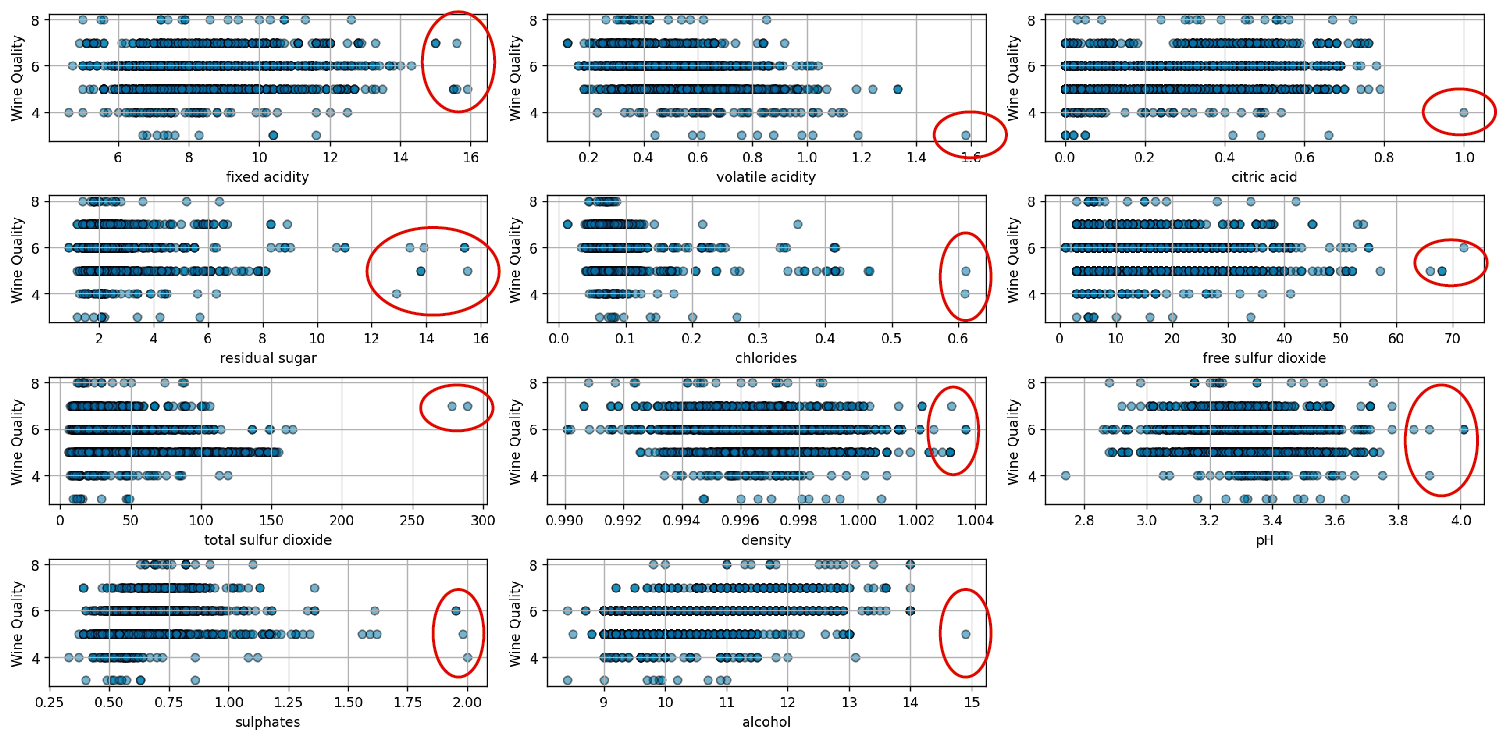
El gráfico se genera utilizando este script. Si bien el método proporciona una visión visual útil, es importante destacar que se basa en una inspección puramente visual. Para determinar con precisión la presencia de outliers, es esencial aplicar principios estadísticos específicos en lugar de confiar únicamente en la observación visual.

Una de las técnicas más utilizadas para identificar y visualizar outliers son los box plots o diagramas de caja. Estos gráficos se emplean frecuentemente en combinación con el método IQR. A continuación, se describe la estructura y las características principales de un diagrama de caja:

1. Mediana (Q2): La línea que divide el cuerpo del diagrama de caja representa la mediana, que es el valor que separa la mitad superior de la mitad inferior de un conjunto de datos. Es una medida de tendencia central y proporciona una idea del valor central de los datos.
2. Cuartiles
   • Primer Cuartil (Q1): También conocido como el cuartil inferior, es el valor que corta el 25% inferior de los datos. Se representa por el borde inferior del cuerpo de la caja.
   • Tercer Cuartil (Q3): También conocido como el cuartil superior, es el valor que corta el 25% superior de los datos. Se representa por el borde superior del cuerpo de la caja.
3. Rango Intercuartílico (IQR): Es la diferencia entre el tercer y el primer cuartil: IQR=Q₃−Q₁. Representa el rango dentro del cual se encuentra la mitad central de los datos.
4. Bigotes: Son las líneas que se extienden desde el cuerpo de la caja hacia arriba y hacia abajo. Generalmente, llegan hasta el dato más extremo dentro del rango definido por Q₁−1.5×IQR y Q₃+1.5×IQR. Los bigotes nos dan una idea de la dispersión de los datos.
5. Outliers: Son los valores que caen fuera del rango definido por los bigotes. En un diagrama de caja, generalmente se representan con puntos individuales fuera de los bigotes. Estos valores son inusualmente altos o bajos en comparación con el resto del conjunto de datos.
6. Cuerpo del Diagrama: Es el rectángulo que se forma entre Q₁ y Q₃. Su ancho es, por lo tanto, el IQR. La forma y tamaño del cuerpo, junto con la posición de la mediana, nos dan una idea sobre la simetría y la dispersión de los datos.

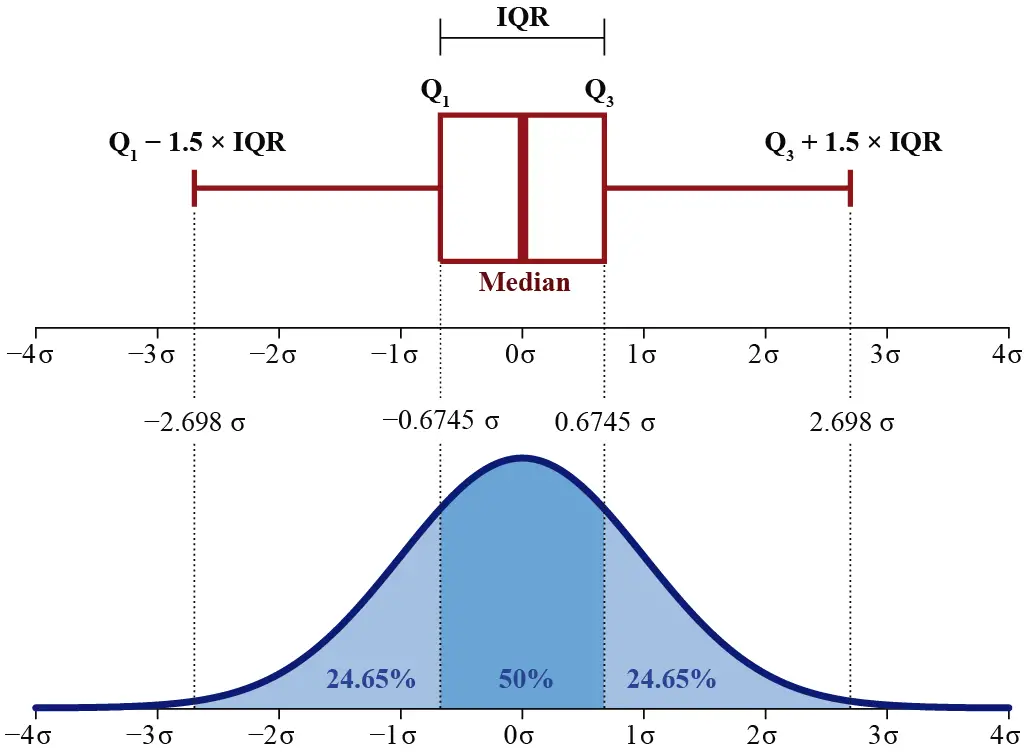
Como vemos en la imagen, para el caso de un conjunto de datos que sigue una distribución normal, el boxplot tiene características específicas en relación con las desviaciones estándar. El Primer Cuartil (Q₁) se sitúa aproximadamente a una desviación estándar de −0.6745 desde la media, mientras que el Tercer Cuartil (Q₃) se ubica cerca de 0.6745 desviaciones estándar desde la media. Esto abarca el Rango Intercuartílico (IQR), que cubre el 50% central de los datos y se extiende aproximadamente 1.35 desviaciones estándar alrededor de la media.

Además, los bigotes del boxplot, que se definen típicamente como 1.5 veces el IQR, se posicionan alrededor de −2.698 y 2.698 desviaciones estándar respecto a la media. En una distribución perfectamente normal, la mayoría de los datos deberían encontrarse dentro de estos límites, y cualquier valor fuera de este rango podría ser considerado un outlier.

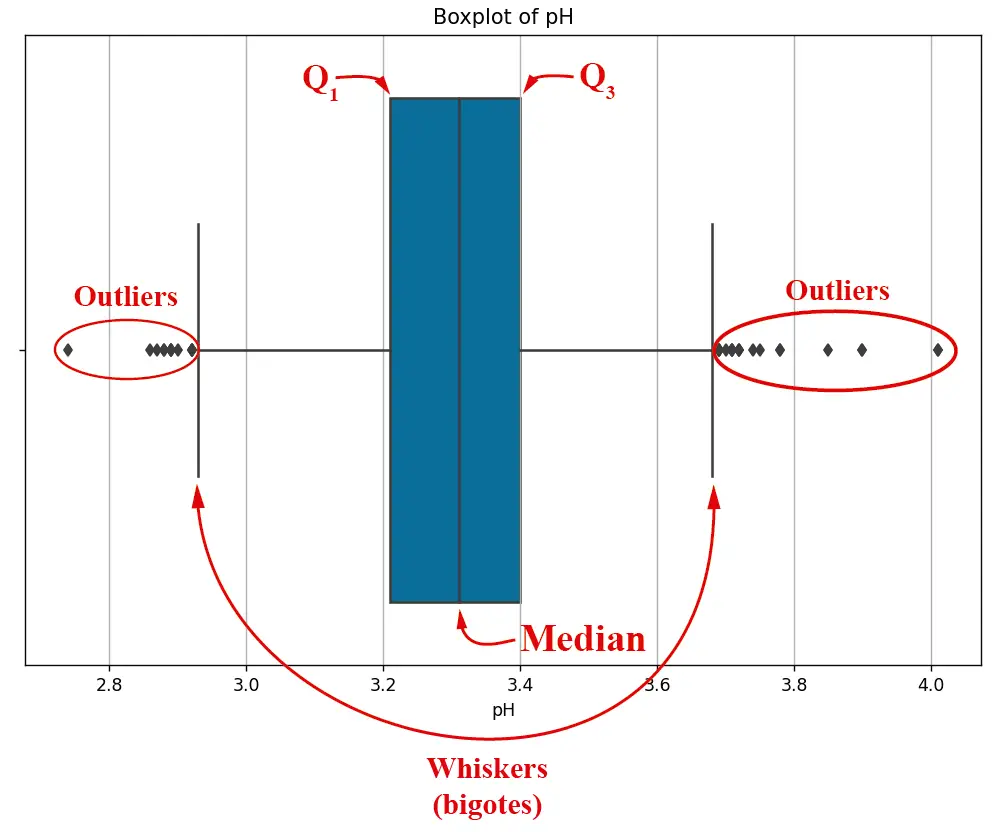
Como vemos en la imagen, para el caso específico del PH tenemos outliers a la izquierda y a la derecha del diagrama de caja. Esta imagen puede construirse con este script. También se puede construir un diagrama de caja para todos y cada uno de los features del dataset:

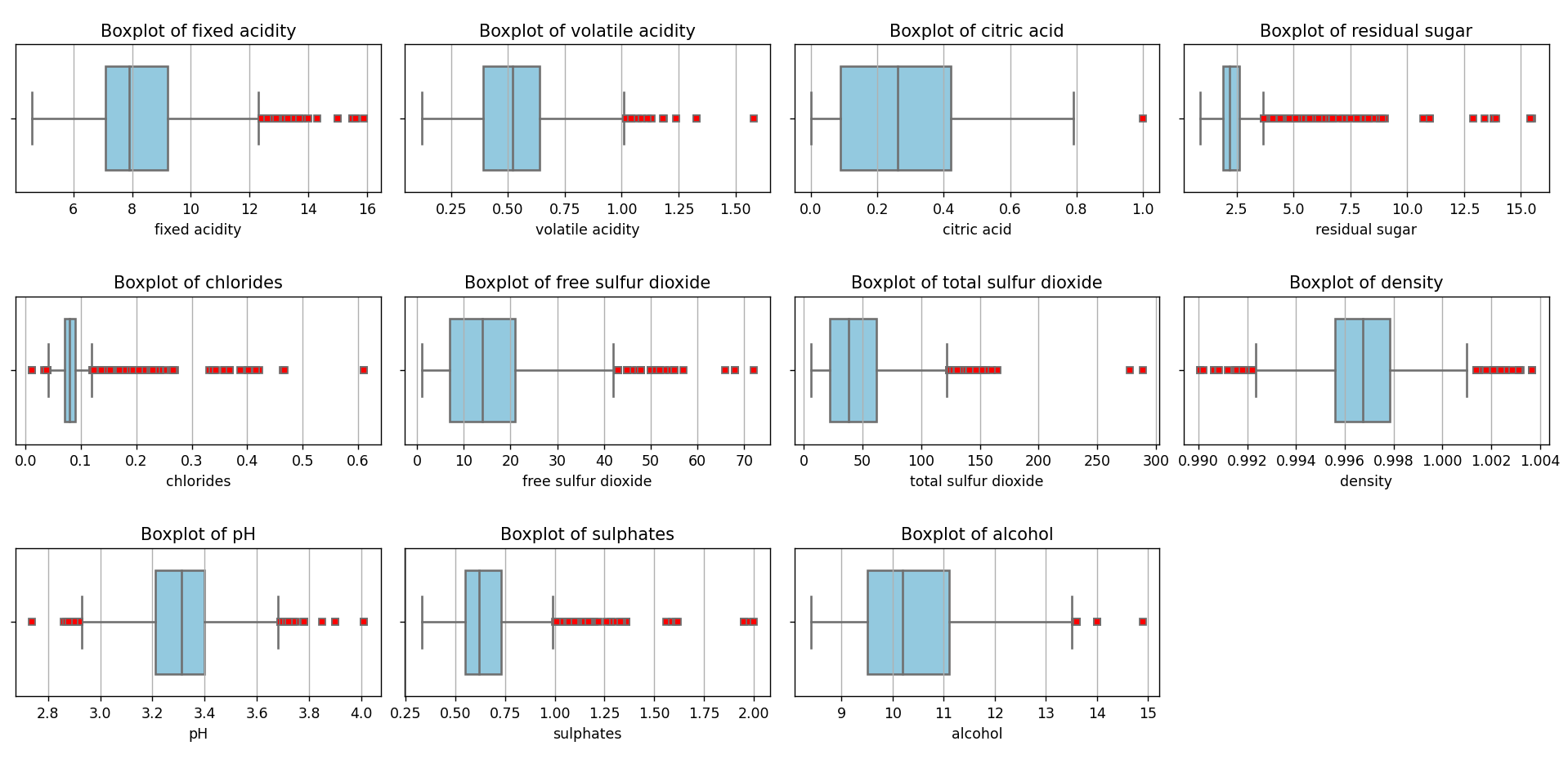
Este gráfico se puede generar utilizando este script. Como vemos, hay una gran cantidad de valores considerados como outliers (color rojo) bajo el criterio del método IQR (Rango Intercuartílico). Los outliers pueden ser considerados como fuente de contaminación en un conjunto de datos, ya que pueden distorsionar las estimaciones y reducir la precisión de los modelos predictivos. Es crucial identificar y gestionar estos valores para garantizar la calidad y la confiabilidad del análisis estadístico y de los modelos de Machine Learning.

Eliminación de Outliers

Hemos analizado diversos métodos para la detección de outliers, aunque nos hemos centrado primordialmente en el uso del Rango Intercuartílico (IQR), complementado con el diagrama de caja para su visualización.

Nuestro siguiente paso consistirá en depurar el dataset, eliminando aquellos valores que se identifican como outliers bajo el criterio del IQR. Esta acción nos proporcionará un nuevo dataset en formato CSV. Posteriormente, aplicaremos el análisis previamente discutido con la finalidad de desarrollar un modelo de Machine Learning. El objetivo es predecir la calidad del vino a partir de sus propiedades físicoquímicas.

Para este propósito, he creado este script. Como resultado, obtenemos un dataset más condensado en relación al original. El nuevo dataset cuenta con 930 registros, en contraposición a los 1599 originales. Esto significa que, tras la eliminación de outliers, hemos conservado aproximadamente el 58% del dataset inicial, es decir, unos 669 registros.

Si volvemos a correr el script que renderiza los diagramas de caja, veremos el siguiente resultado:

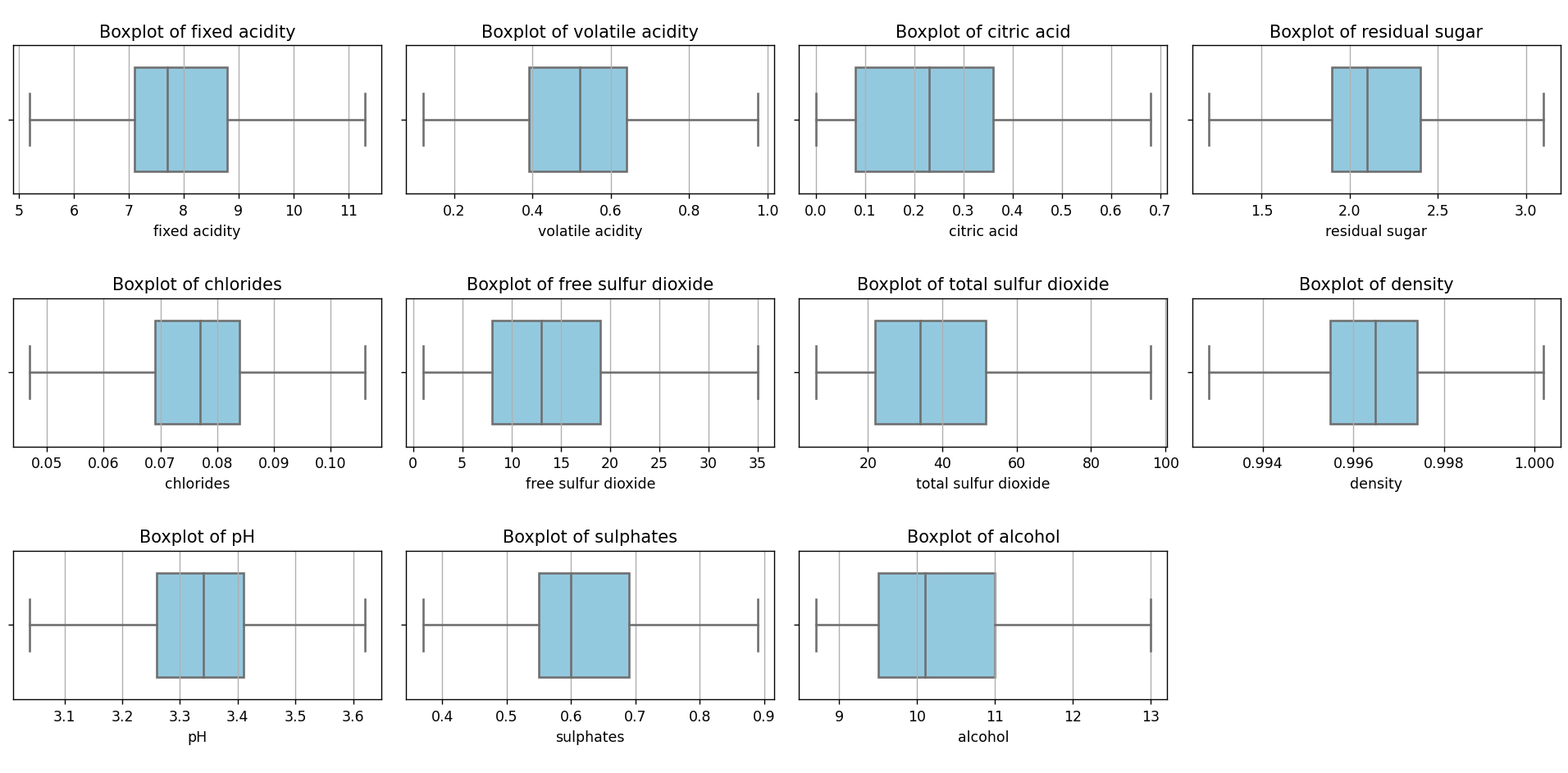
Como vemos, ya no hay outliers. Lo mismo sucede si vemos los histogramas de frecuencia:

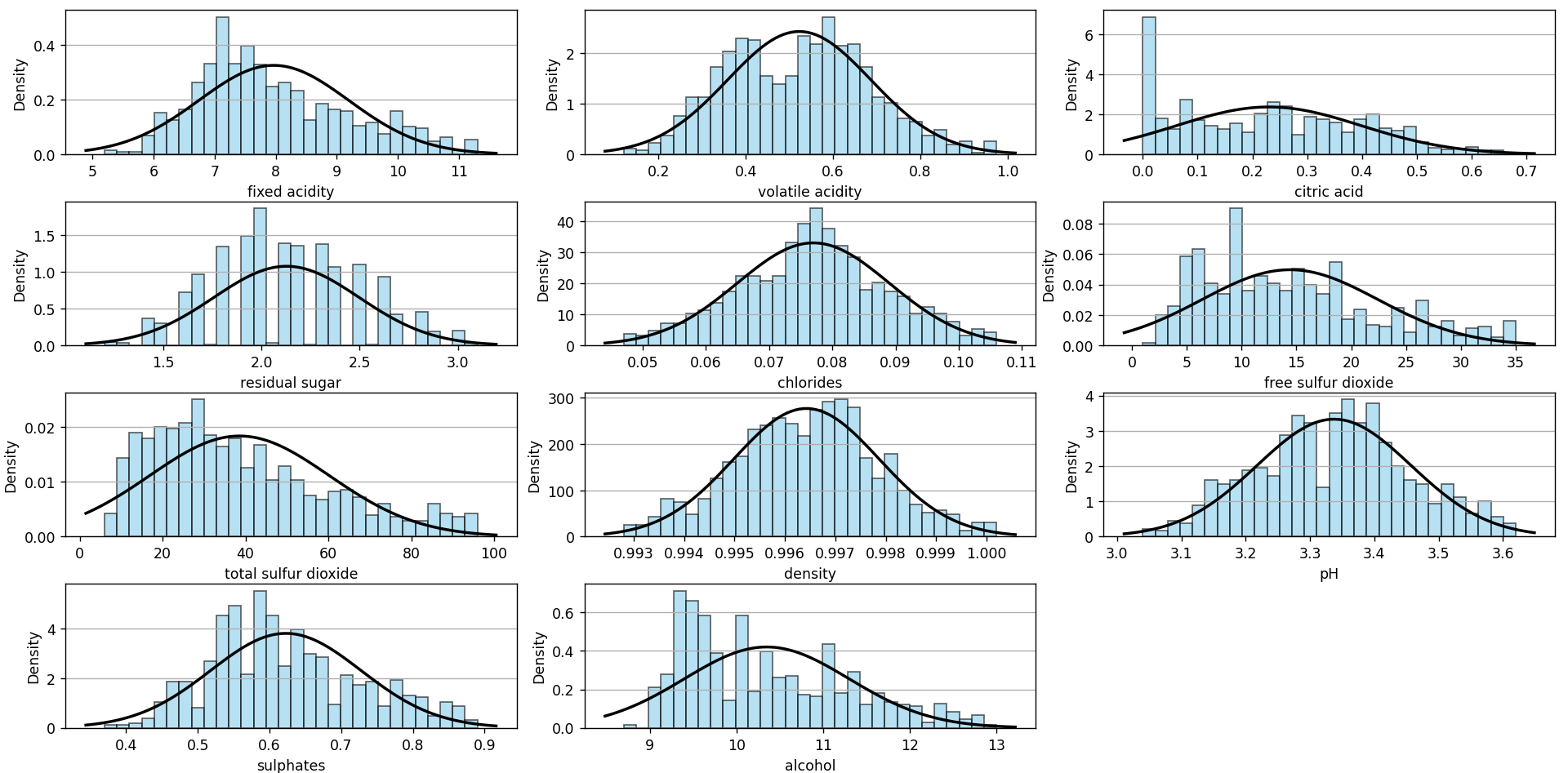
Visto de esta forma, pareciera que la densidad y los cloruros se acercan bastante a una distribución normal. Les apliqué el test de Shapiro-Wilk y resultó negativo, pero no nos concentraremos en eso en este momento.

Lo que me ha llamado la atención luego de hacer este análisis es la proporción elevada de outliers que tuvieron que ser eliminados, lo que sugiere que los datos pueden haber sido influenciados por factores extremos o que la naturaleza de la producción del vino es inherentemente variable. Sin embargo, es esencial recordar que la eliminación masiva de outliers podría conllevar la pérdida de información valiosa. Aunque es crucial asegurarse de que los modelos no estén sesgados por estos valores extremos, también es vital entender la causa subyacente de estos outliers antes de tomar decisiones definitivas sobre su eliminación.

Por lo pronto trabajaremos con lo que tenemos. Tengo curiosidad sobre lo que pasará cuando probemos los algoritmos de Machine Learning con este dataset. En futuras publicaciones espero contrastar los resultados de la utilización del IQR con los otros métodos que mencionamos previamente.

Probando algoritmos de Machine Learning

En mi post anterior presenté una metodología para identificar el mejor algoritmo de clasificación utilizando un 10-fold cross validation junto con un gridsearch de algoritmos de clasificación. Vamos a ver como nos va ahora.

Primero voy a intentar con los algoritmos de regresión. Estos son los resultados:

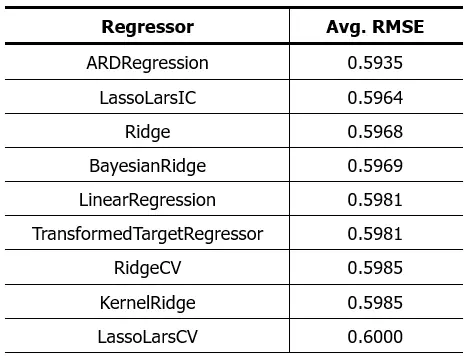
El resultado previo había sido este:

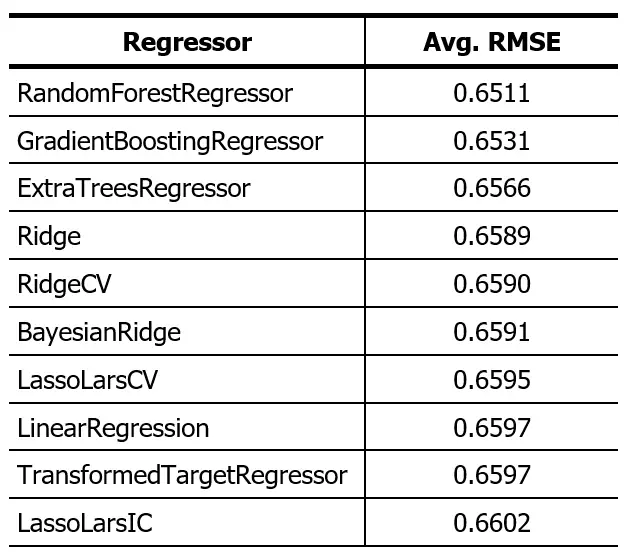La reducción en el RMSE significa que el error en la predicción se ha reducido. Eso significa que los algoritmos presentados funcionan mejor que los del post anterior, lo cual era de esperar luego de eliminar los valores fuera de rango.

Si decidimos redondear los resultados de los algoritmos de regresión y evaluar los resultados como si se tratase de un algoritmo de clasificación, veremos el siguiente resultado:

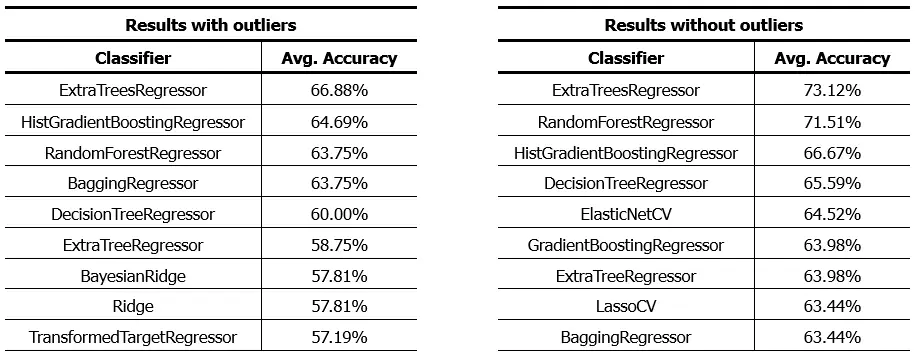
Como vemos, los algoritmos con el mejor performance son básicamente los mismos, pero con un mejor performance. Un aumento de aproximadamente 6% en la precisión de los algoritmos. Estos resultados los podemos lograr con este script, simplemente seleccionando uno u otro dataset.

Es importante señalar que, aunque hemos logrado mejorar la precisión de nuestros modelos, la eliminación de outliers también tuvo un impacto en la distribución de las clases en el dataset. Tras la depuración, algunas clases quedaron con un número muy reducido de muestras. Esto puede ser problemático, especialmente al aplicar algoritmos de clasificación, ya que una representación insuficiente de ciertas clases en el conjunto de datos puede llevar a un desempeño deficiente del modelo en esas categorías específicas.

En esencia, el modelo podría no estar bien entrenado para reconocer y clasificar correctamente esas clases subrepresentadas. Por lo tanto, antes de proceder con algoritmos de clasificación, es esencial analizar y, si es necesario, equilibrar la distribución de las clases para asegurar un entrenamiento robusto y resultados confiables.

Conclusiones

A lo largo de este artículo, abordamos la importancia de identificar y gestionar los outliers en un conjunto de datos. Estas observaciones atípicas, si no se manejan adecuadamente, pueden distorsionar significativamente el análisis y afectar la precisión y fiabilidad de los modelos predictivos. Algunas conclusiones clave de nuestro análisis incluyen:

• • Relevancia de los Outliers: Las observaciones atípicas pueden surgir por diversas razones, ya sea por errores humanos, fallos en los instrumentos de medición, o incluso por variaciones genuinas en una población. Identificar la causa subyacente de estos outliers es crucial antes de tomar decisiones sobre su tratamiento.
  • Métodos de Identificación: Si bien hay múltiples técnicas para identificar outliers, el método IQR y los diagramas de caja resultaron ser herramientas eficaces en nuestro análisis del Red Wine Quality Dataset. Sin embargo, es esencial combinar métodos visuales con técnicas analíticas para una identificación precisa.
  • Impacto en el Modelado: La eliminación de outliers llevó a una mejora significativa en la precisión de los modelos de regresión aplicados al dataset. Sin embargo, es crucial tener en cuenta el equilibrio entre mejorar la precisión y perder información potencialmente valiosa.
  • Limitaciones en la Clasificación: A pesar de las mejoras observadas en la regresión, la eliminación de outliers también tuvo un impacto en la distribución de clases, lo que podría afectar el rendimiento de los algoritmos de clasificación. Las clases subrepresentadas requieren una atención especial para garantizar un modelado adecuado.
  • Exploración de Otras Técnicas: Aunque el método IQR proporcionó resultados significativos en este análisis, es esencial considerar y explorar otras técnicas para la identificación y eliminación de outliers. Existen múltiples enfoques, como el Z-Score, métodos de clustering como K-Means y DBSCAN, y técnicas basadas en redes neuronales como Autoencoders. Cada técnica tiene sus fortalezas y debilidades y puede ser más adecuada dependiendo de la naturaleza y estructura del conjunto de datos. En futuros análisis, examinaremos estas opciones en detalle para obtener una comprensión más completa de cómo gestionar eficazmente los outliers.

En resumen, mientras que la gestión de outliers es un aspecto esencial del análisis de datos, es crucial abordar este proceso con cuidado y consideración. Cada paso, desde la identificación hasta la eliminación o ajuste de outliers, debe hacerse con una comprensión clara del conjunto de datos y del contexto general del análisis.

Espero que esta información les sea de utilidad. Cualquier duda o comentario me lo hacen llegar a través de la caja de comentarios.