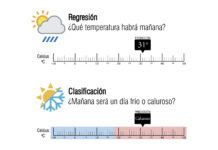
El análisis de datos y la construcción de modelos de Machine Learning requieren no solo datos limpios, sino también datos estructurados de manera óptima. Uno de los pasos más críticos en en el preprocesamiento de un dataset es la normalización de datos.
Al igual que identificar y gestionar los outliers es vital para la calidad de un modelo, la normalización garantiza que nuestras características (o variables) sean comparables y no sesguen indebidamente nuestros resultados.
¿Qué es la normalización de Datos?
La normalización de datos es un proceso fundamental en el preprocesamiento de datos, cuyo objetivo es ajustar la escala de las características numéricas para que sean comparables entre sí. A menudo, se refiere a la transformación de datos para que tengan un rango específico, como entre 0 y 1.
Sin embargo, es esencial distinguir entre normalización y estandarización: mientras que la primera ajusta los valores dentro de un rango definido, la estandarización reescala los datos para que tengan una media de 0 y una desviación estándar de 1.
La importancia de la normalización en el procesamiento de datos
Recientemente, compartí con ustedes un artículo sobre el Modelado Matemático del Algoritmo KNN, en el cual profundizamos en los procedimientos de regresión y clasificación que dependen del cálculo de distancias entre las características de un conjunto de datos.
En ese artículo, usamos el Red Wine Dataset como base para nuestro análisis, presentando específicamente dos registros que se muestran a continuación:
Para determinar la distancia entre las muestras, utilizamos la siguiente ecuación:
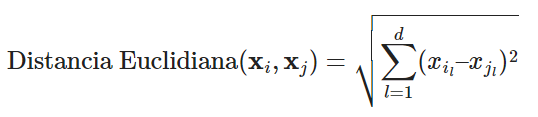
Desglosando esta ecuación, realizamos una serie de operaciones matemáticas detalladas a continuación:

Finalmente, sumamos estos valores dentro de una raíz cuadrada para obtener la distancia:
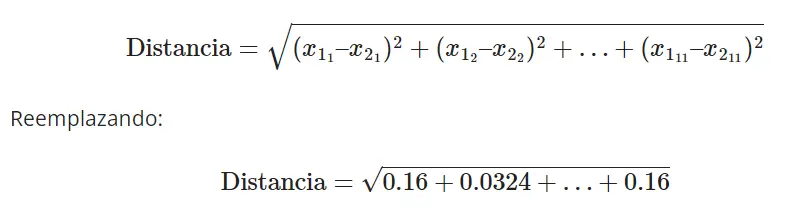
Aquí es donde surge un desafío crítico: la disparidad en la escala de los diferentes features. La acumulación de las diferencias dentro de la raíz cuadrada puede verse dominada por ciertas características debido a su escala. Observando de cerca, notamos que el cuadrado de la diferencia entre los features 6 y 7 suma 196 y 1086, respectivamente. Estos números eclipsan significativamente a las otras características que tienen valores más pequeños, entre 0 y 1. Este desequilibrio puede sesgar los resultados y afectar la precisión del algoritmo.
Es aquí donde la normalización de datos se vuelve esencial. Al normalizar, aseguramos que cada característica tenga el mismo peso en el cálculo de la distancia, permitiendo que el algoritmo funcione de manera óptima. La normalización transforma todos los valores a una escala común, generalmente entre 0 y 1, eliminando así cualquier sesgo introducido por la magnitud y escala de las características.
Métodos Comunes de Normalización
Min-Max Scaling (escalado Min-Max)
El método de Min-Max Scaling, también conocido como Escalado Min-Max, es una técnica utilizada para transformar características numéricas para que todos los valores estén dentro de un rango específico, generalmente entre 0 y 1. Es especialmente útil cuando las características tienen diferentes rangos y deseamos estandarizarlos a una escala común.
La transformación se realiza utilizando la siguiente fórmula:
\[ X_{\text{norm}} = \frac{X – X_{\text{min}}}{X_{\text{max}} – X_{\text{min}}} \]
Donde:
- \( X \): es el valor original de la característica.
- \( X_{\text{min}} \): es el valor mínimo de la característica en el conjunto de datos.
- \( X_{\text{max}} \): es el valor máximo de la característica en el conjunto de datos.
- \( X_{\text{norm}} \): es el valor normalizado.
Supongamos que tenemos un conjunto de datos con valores que varían entre 10 y 50, y queremos normalizar un valor específico, digamos 30. Usando la fórmula de Min-Max Scaling:
\[ X_{\text{norm}} = \frac{30 – 10}{50 – 10} = \frac{20}{40} = 0.5 \]
Por lo tanto, el valor normalizado de 30 es 0.5.
Aunque el Min-Max Scaling es efectivo para llevar todas las características a una escala común, tiene algunas limitaciones:
-
- Es sensible a valores atípicos (outliers). Un valor atípico extremo en la característica puede reducir el efecto de escalamiento de otros valores.
- No maneja bien las distribuciones que no son uniformes.
A pesar de estas limitaciones, el Min-Max Scaling es ampliamente utilizado en la práctica debido a su simplicidad y efectividad en muchos escenarios. Es importante entender los datos y el contexto antes de decidir qué técnica de normalización o estandarización usar.
Z-score Normalization (Normalización de Puntuación-Z)
La normalización de Puntuación-Z, o Z-score Normalization, es una técnica de estandarización que reescala características numéricas de manera que tengan una media de 0 y una desviación estándar de 1. Es especialmente útil para algoritmos que asumen que todas las características tienen una distribución normal, o cuando se desea comparar características con diferentes unidades o escalas.
La transformación se realiza utilizando la siguiente fórmula:
\[ X_{\text{norm}} = \frac{X – \mu}{\sigma} \]
Donde:
- \( X \): es el valor original de la característica.
- \( \mu \): es la media de la característica.
- \( \sigma \): es la desviación estándar de la característica.
- \( X_{\text{norm}} \): es el valor estandarizado o normalizado.
Supongamos que tenemos un conjunto de datos con edades que tienen una media de 30 años y una desviación estándar de 10 años. Si queremos estandarizar una edad específica, digamos 45 años, usando la fórmula de Puntuación-Z:
\[ X_{\text{norm}} = \frac{45 – 30}{10} = 1.5 \]
Esto significa que la edad de 45 años está 1.5 desviaciones estándar por encima de la media.
La normalización de Puntuación-Z es muy útil, pero tiene algunas consideraciones:
-
- No cambia la forma de la distribución de los datos. Solo cambia la escala.
- Es sensible a valores atípicos. Un valor atípico extremo puede afectar significativamente la media y la desviación estándar, y por lo tanto, la estandarización.
- No necesariamente restringe los valores a un rango específico, como [0, 1]. Los valores pueden ser menores que -1 o mayores que 1.
A pesar de estas consideraciones, la normalización de Puntuación-Z es ampliamente utilizada en la práctica por su capacidad para manejar características con diferentes escalas y distribuciones.
Escalado Decimal
El método de Escalado Decimal es una técnica de normalización que busca ajustar la magnitud de los datos al desplazar el punto decimal. A diferencia de otros métodos que suelen transformar los datos a un rango específico, como [0,1], el Escalado Decimal tiene como principal objetivo reducir la magnitud de los datos a una escala manejable, lo que puede ser útil en situaciones en las que se manejan números extremadamente grandes o pequeños.
La fórmula para el Escalado Decimal es:
\[ X_{\text{norm}} = \frac{X}{10^j} \]
Donde:
- \( X \): es el valor original de la característica.
- \( j \): es el número mínimo de dígitos del valor más grande en la característica, excluyendo el punto decimal.
- \( X_{\text{norm}} \): es el valor normalizado.
Por ejemplo, supongamos que el valor más grande en nuestro conjunto de datos es 853. En este caso, \( j \) sería 3 porque 853 tiene tres dígitos. Si quisiéramos normalizar el valor 532 utilizando el Escalado Decimal, aplicaríamos la fórmula:
\[ X_{\text{norm}} = \frac{532}{10^3} = 0.532 \]
Así, el valor 532 se convierte en 0.532 después de aplicar el escalado decimal.
Una de las ventajas del Escalado Decimal es su simplicidad y la capacidad de reducir rápidamente la magnitud de los datos. Sin embargo, es importante notar que, a diferencia de otros métodos de normalización, el Escalado Decimal no garantiza que los datos transformados se encuentren en un rango específico. Por lo tanto, es esencial entender el contexto y los requisitos del problema antes de elegir este método de normalización.
En resumen, el Escalado Decimal es una herramienta útil para manejar datos con magnitudes muy variadas, pero se debe proceder con precaución y considerar otros métodos de normalización si se requiere un rango específico para los datos transformados.
Normalización L2 (Norma Euclidiana)
La normalización L2, también conocida como normalización de la norma euclidiana, es una técnica que modifica la escala de un vector de características de manera que su longitud (o magnitud) sea 1. Este método se basa en la distancia euclidiana, que es la distancia «en línea recta» entre dos puntos en un espacio euclidiano.
La distancia euclidiana entre dos puntos \( P \) y \( Q \) en un espacio n-dimensional se calcula como:
\[ d(P, Q) = \sqrt{(p_1 – q_1)^2 + (p_2 – q_2)^2 + … + (p_n – q_n)^2} \]
La fórmula para la normalización L2 es:
\[ X_{\text{norm}} = \frac{X}{\sqrt{X_1^2 + X_2^2 + … + X_n^2}} \]
Donde:
- \( X \): es el vector original de características.
- \( X_1, X_2, … X_n \): son los componentes individuales de ese vector.
- \( X_{\text{norm}} \): es el vector normalizado.
La idea detrás de esta normalización es llevar el vector \( X \) a la «superficie» de una esfera unitaria. Después de aplicar la normalización L2, la suma de los cuadrados de los elementos del vector será exactamente 1.
Por ejemplo, suponga que tiene un vector \( X = [3, 4] \). La longitud (o magnitud) de este vector es 5, que es la hipotenusa de un triángulo rectángulo con lados de longitud 3 y 4. Si aplica la normalización L2:
\[ X_{\text{norm}} = \frac{[3,4]}{\sqrt{3^2 + 4^2}} = \frac{[3,4]}{5} = [0.6, 0.8] \]
El vector resultante tiene una longitud de 1 y apunta en la misma dirección que el vector original.
La normalización L2 es útil en varias aplicaciones en Machine Learning. También se utiliza en la búsqueda y recuperación de información para normalizar documentos en la representación de bolsa de palabras. Esta técnica asegura que los datos se escalen de manera que la longitud total del vector de características sea 1, lo que puede ser útil en muchos algoritmos que dependen de la magnitud de los datos.
Normalización Logarítmica
La normalización logarítmica es una técnica utilizada para transformar datos que tienen un sesgo en su distribución. Es comúnmente empleada cuando los datos presentan una distribución exponencial o cuando existe una amplia gama de valores en la característica. Al aplicar una transformación logarítmica, los valores extremadamente altos se comprimen y los valores bajos se expanden, reduciendo así la variabilidad causada por valores atípicos extremos.
La fórmula para la normalización logarítmica es:
\[ X_{\text{norm}} = \log(X) \]
Donde:
- \( X \): es el valor original de la característica.
- \( X_{\text{norm}} \): es el valor transformado.
Es importante tener en cuenta que esta transformación solo es aplicable para valores positivos de \( X \), ya que el logaritmo de un número no positivo no está definido en los números reales. Si los datos originales contienen valores no positivos, se puede aplicar un pequeño desplazamiento (por ejemplo, sumar una constante) para garantizar que todos los valores sean positivos antes de aplicar la transformación logarítmica.
Un ejemplo práctico de la utilidad de la normalización logarítmica se encuentra en el análisis de datos financieros, donde ciertas características, como los ingresos o los valores de mercado, pueden variar en órdenes de magnitud entre diferentes entidades. Aplicando una transformación logarítmica, se puede reducir el sesgo y mejorar la interpretabilidad de los datos.
Integración en Python
Planeo ilustrar cómo implementar estas técnicas de normalización en Python, tomando como ejemplo el Red Wine Quality Dataset. No obstante, abordar este tema aquí haría que este artículo fuera demasiado extenso. Por ello, he decidido dedicarle un post independiente.
Conclusión
La normalización desempeña un papel crucial en el ámbito del análisis de datos y el Machine Learning, permitiendo que los algoritmos funcionen de manera eficiente y precisa. Cada técnica de normalización tiene sus propios méritos y aplicaciones ideales, dependiendo del tipo de datos y del problema específico que se esté abordando.
Es vital comprender las características y las distribuciones de los datos para seleccionar el método más adecuado. Además, siempre es recomendable experimentar con diferentes técnicas y evaluar el rendimiento del modelo resultante. Con una adecuada preparación y estructuración de los datos, podemos maximizar la eficacia de nuestros algoritmos y obtener insights más profundos y precisos a partir de nuestros conjuntos de datos.
¡Gracias por leer este artículo! Espero que haya sido de utilidad y haya aclarado tus dudas sobre la normalización en el análisis de datos. Si tienes alguna pregunta, comentario o sugerencia, ¡no dudes en dejarla en la sección de comentarios!