En este post voy a explicar, paso por paso, como construir un algoritmo de Machine Learning para clasificar imágenes de números manuscritos. Es decir, haremos un programa al cual le pasaremos una lista de imágenes y éste se encargará de decirnos si se trata de un número entre 0 y 9.
Para ello utilizaremos el MNIST dataset, sobre el cual ya hemos escrito previamente en este blog:
En estas entradas lo que hemos hecho es explorar las características del dataset MNIST y en cómo podemos cargar los pixeles que forman cada una de las imágenes en un programa en Python.
Esta vez lo que haremos será entrenar un clasificador, específicamente un Support Vector Machine, para que nuestro programa pueda discriminar las imágenes y decirnos si se trata de un 0, 1, 2, 3… 8 o 9.
Pero antes de empezar a escribir y probar código, hay algunos conceptos que necesitamos definir para poder entender lo que haremos después.
¿Qué es Machine Learning?
Básicamente se trata de un paradigma que busca lograr que las computadoras «aprendan» a realizar tareas repetitivas complejas. Se dice que un algoritmo «aprende» cuando su desempeño mejora con la experiencia y mediante el uso de datos.
Contrario a lo que mucha gente piensa, el concepto de Machine Learning no es nada nuevo. Ya desde finales de la década de 1950 se hablaba sobre el concepto, y en la década de los 60 ya se estaban desarrollando algoritmos de clasificación en este campo.
Sin embargo, el estudio y aplicación de algoritmos de Machine Learning fue algo casi exclusivo de unos cuantos grupos de investigación durante muchos años. No fue sino hasta el Siglo XXI cuando se produjo la universalización del paradigma y las técnicas utilizadas en Machine Learnign, las cuales del público en general. Hoy en día no hace falta ser un científico o dedicar años a la investigación en estadística y/o ciencias computacionales para implementar un algoritmo de inteligencia artificial en un proceso cualquiera.
Sobre este tema me gustaría escribir un artículo completo dedicado al describir el paradigma de Machine Learning y definir conceptos como Data Science, Deep Learning, Machine Learning, entre otros. Sin embargo, por el momento haré esta publicación con la breve introducción que acabamos de hacer. Hay mucho por explicar, muchos conceptos por definir y muchas dudas por aclarar, pero para la implementación de un algoritmo sencillo de Machine Learning no necesitamos saber nada de eso.
Por lo pronto definiremos un clasificador de Machine Learnign como un modelo matemático que nos permite clasificar conjuntos de datos utilizando modelos matemáticos probabilísticos. Estos modelos han sido convertidos en algoritmos computacionales, los cuales nos permiten realizar tareas que podrían parecer complicadas, de una manera relativamente sencilla.
Support Vector Machine
Mucha gente piensa que cuando hablamos de Machine Learning o de Inteligencia Artificial estamos haciendo referencia directa a redes neuronales. Esto no es necesariamente cierto, pues las redes neuronales no son el único modelo de Machine Learning que existe.
El Support Vector Machine (SVM) es un modelo de aprendizaje asistido para la clasificación de datos y el análisis de regresiones. Aprendizaje asistido significa que para el entrenamiento del modelo hace falta alimentarlo con datos conocidos y etiquetados.
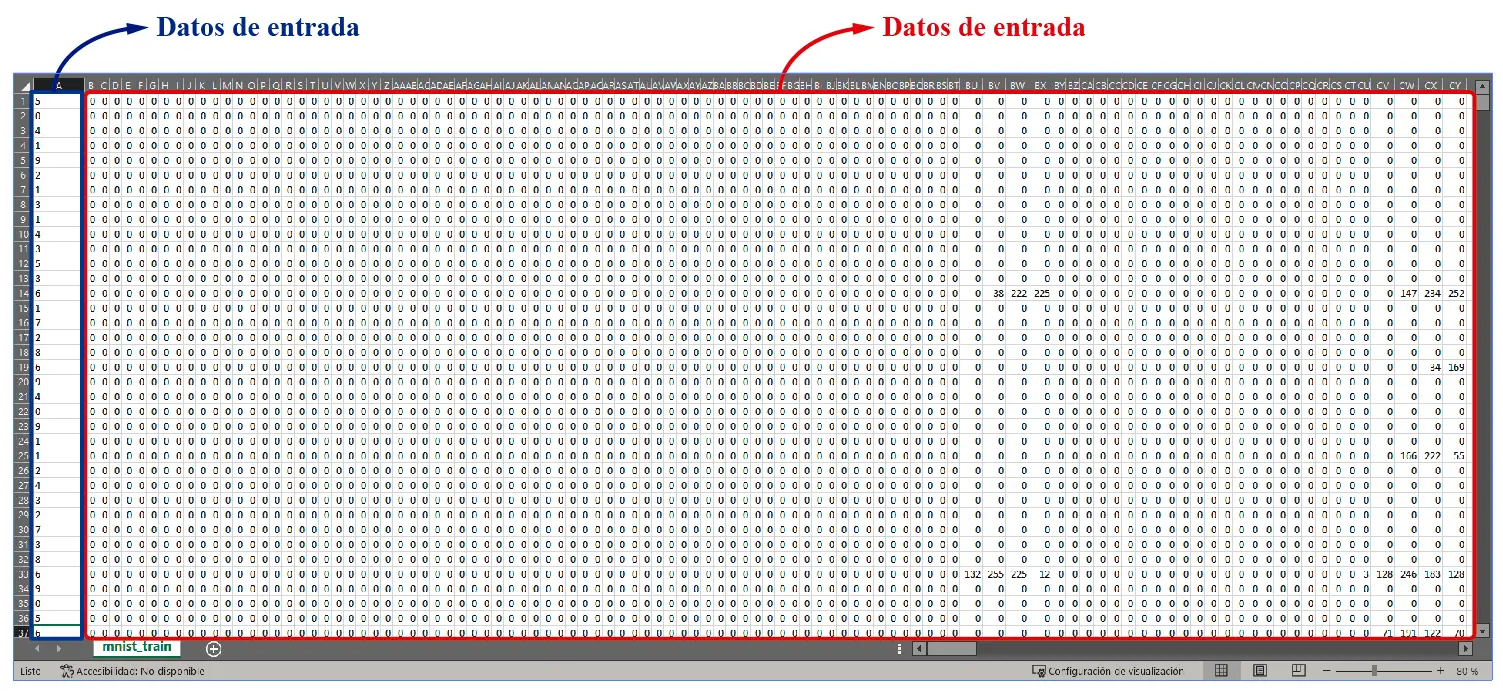

Los números enmarcados en rojo son los datos de entrada del algoritmo. Cada fila contiene 784 pixeles que forman las imágenes de los números manuscritos, los cuales son imágenes en formato 28 x 28 pixeles. Como hemos mencionado en post anteriores, las imágenes del dataset MNIST lucen así:
Cada cuadrito de esos es una imagen 28 x 28. Cada columna en la hoja de Excel mostrada arriba es uno de esos pixeles. Si se convierten esos datos en una matriz, podemos pasarlas como parámetros de aprendizaje en un modelo de Machine Learning.
Los datos enmarcados en azul son las etiquetas. Como estamos trabajando con modelos de aprendizaje asistido, necesitamos decirle al algoritmo qué número representa cada imagen, para que este «aprenda a reconocerlas». Esto lo logramos con las etiquetas, indicándole al algoritmo qué numero representa cada conjunto de 784 pixeles. Este concepto quedará mejor explicado en la siguiente sección, cuando utilicemos códigos en Python para probar la teoría.
Detrás del concepto de un Support Vector Machine existe toda una teoría que se fundamenta en conceptos de probabilidad y estadística, la cual sería muy difícil de explicar en un post del tipo técnico, como este. Espero dedicar un post entero a explicar el concepto en algún momento.
Codificanto un SVM en Python
Para codificar un SVM en Python podemos utilizar la librería Sklearn, una de las más populares en este tema. El script que utilizaré para hacer las pruebas de concepto lo pueden encontrar en este enlace.
El código es el siguiente:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 |
import pandas as pd import numpy as np import time as time from sklearn import svm trainingSamples = 50000 # Self explanatory testingSamples = 10000 """ Here I set the global variables, which will be used to test the computing time for both training and testing """ startTrainingTime = 0 endTrainingTime = 0 trainingTime = 0 startTestingTime = 0 endTestingTime = 0 testingTime = 0 def loadDataset(fileName, samples): # A function for loading the data from a dataset x = [] # Array for data inputs y = [] # Array for labels (expected outputs) train_data = pd.read_csv(fileName) # Data has to be stored in a CSV file, separated by commas y = np.array(train_data.iloc[0:samples, 0]) # Labels column x = np.array(train_data.iloc[0:samples, 1:]) / 255 # Division by 255 is used for data normalization return x, y def main(): train_x, train_y = loadDataset("../datasets/mnist/mnist_train.csv", trainingSamples) # Loading training data test_x, test_y = loadDataset("../datasets/mnist/mnist_test.csv", testingSamples) # Loading testing data clf = svm.SVC() # Classifier object startTrainingTime = time.time() clf.fit(train_x, train_y) # Training of a model by fitting training data to object endTrainingTime = time.time() trainingTime = endTrainingTime - startTrainingTime # Training time calculation validResults = 0 startTestingTime = time.time() for i in range(len(test_y)): # A for loop to evaluate result vs expected results expectedResult = int(test_y[int(i)]) # Load expected result from testing dataset result = int( clf.predict(test_x[int(i)].reshape(1, len(test_x[int(i)])))) # Calculate a result using trained model outcome = "Fail" if result == expectedResult: validResults = validResults + 1 # Counting valid results outcome = " OK " print("Expected result: ", expectedResult, " | Obtained result: ", result, " | ", outcome, " | Accuracy: ", round((validResults / (i + 1)) * 100, 2), "%") # Printing the results for each label in testing dataset endTestingTime = time.time() testingTime = endTestingTime - startTestingTime # Calculation of testing time print("-------------------------------") print("Results") print("-------------------------------") print("Training samples: ", trainingSamples) print("Training time: ", round(trainingTime, 2), " s") print("Testing samples: ", testingSamples) print("Testing time: ", round(testingTime, 2), " s") print("Testing accuracy: ", round((validResults / testingSamples) * 100, 2), "%") if __name__ == "__main__": main() |
Sobre este código, tengo las siguientes observaciones:
- Como ya mencioné, la librería utilizada para este ejemplo es Skelarn. Existen muchas otras, pero esta me ha resultado especialmente fácil de utilizar.
- El código está bien documentado. Cada instrucción cuenta con su comentario, que explica lo que se está haciendo con cada instrucción.
- El script y los datasets utilizados para las pruebas se encuentran disponibles en nuestro reposotorio de Machine Learning en Github.
- La función loadDataset es la que nos permite cargar los datos del MNIST desde un archivo CSV. Esto ya lo explicamos en la publicación Importar archivos CSV en Python.
- Para poder probar este código hace falta que el script sea colocado en una carpeta específica, al igual que los archivos CSV.
La siguiente imagen presenta la estructura que se debe utilizar para que funcione.
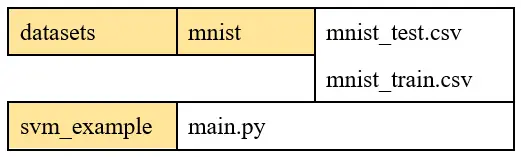
Es decir, el script, al que he llamado main.py, debe colocarse en una carpeta llamada svm_cample. Se debe colocar otra carpeta llamada datasets en la misma en la que se ha guardado la carpeta svm_example. Dentro de datasets se coloca una carpeta llamada mnist y dentro de ésta los archivos CSV.
Otra opción podría ser cambiar las direcciones a los ficheros en el código o «clonar» el repositorio completo desde Github.
Cuando se ejecute el código aquí presentado iniciará el entrenamiento del Support Vector Machine. El tiempo que se tardará el algoritmo en completar el entrenamiento dependerá de las capacidades de hardware de la computadora en la que se ejecute el algoritmo. En mi caso, yo trabajo desde mi laptop, una MSI con 32 GB de RAM y un Intel Core i7 con 4 núcleos físicos, 8 núcleos lógicos y 2.80 GHz. Con este hardware, el resultado es el siguiente:
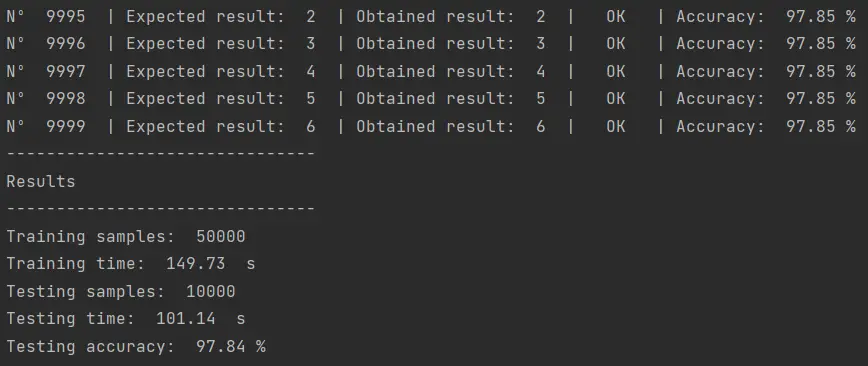
El entrenamiento demoró casi 150 segundos, unos 2 minutos y medio. El tiempo de pruebas fue de 101 segundos y la precisióon fue de 97.84%.
¿Qué representa la precisión del algoritmo?
Como vemos en la imagen anterior, para todos y cada uno de los datos del mnist_test.csv se realiza una prueba. Luego de que el modelo ha sido entrenado, le pasamos los datos de prueba a ver si logramos predecir el número contenido en las imágenes de prueba.
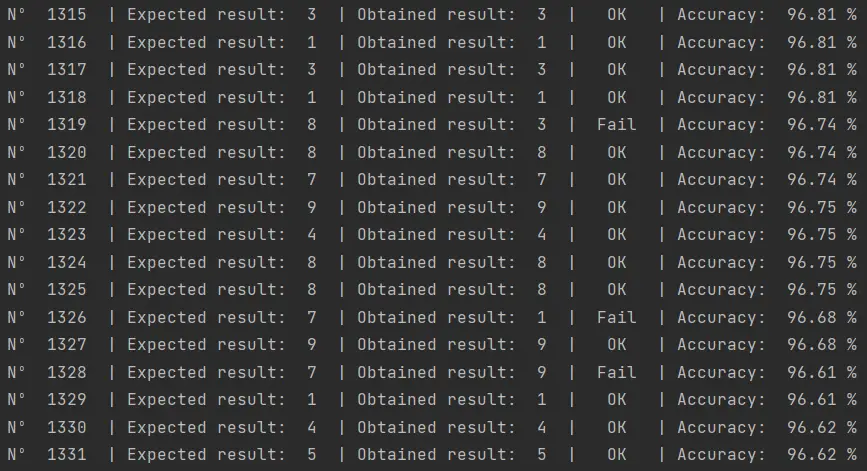
En la imagen, por ejemplo, vemos que en la prueba 1319 el algoritmo falló, confundiendo un 8 con un 3. En el 1326 falló confundiendo el 1 con un 7 y en el 1328 confundió el 9 con un 7. Sin embargo, si utilizamos el algoritmo de renderizado de imágenes para el MNIST dataset para reconstruir las imágenes en cuestión, podremos ver lo siguiente:

Como vemos, el algoritmo se equivocó en imágenes que lucen dudosas incluso para nosotros como seres humanos. Es probable que si revisamos el resto de las imágenes en las que el algoritmo se equivocó veremos ambigüedades similares.
En total el algoritmo identificó correctamente un total de 9784 imágenes y se equivocó en 216. Decimos que se «equivocó», pero probablemente se trata de imágenes con alguna característica que se presta para una mala interpretación.
Mejorando la precisión del clasificador
Es posible mejorar la precisión del algoritmo modificando los parámetros de la función kernel utilizada con el Support Vector Machine.
Una función kernel es un método utilizado para tomar datos como entrada y transformarlos en la forma requerida de procesamiento de datos. Las funciones kernel son un conjunto de funciones matemáticas utilizadas en la Support Vector Machines como una ventana para la manipulación de datos. Generalmente transforman el conjunto de datos de entrenamiento para que una superficie de decisión no lineal pueda transformarse en una ecuación lineal en una mayor cantidad de espacios de dimensión.
Como ya he mencionado antes, la teoría detrás de los Support Vector Machines tiene toda una explicación basada en modelos matemáticos probabilísticos, tema del que espero escribir en algún momento en los próximos meses. Las funciones kernel forman parte importante de esa explicación, por lo que en este momento no entraré en mayores detalles sobre estas funciones.
Por lo pronto pensemos en las funciones kernel como parámetros configurables de nuestro algoritmo de clasificación basado en Support Vector Machine.
Existen 4 tipos básicos de funciones kernel que se pueden utilizar con un SVM:
- Lineal
- Polinomial
- RBF (radial basis function o función de base radial)
- Sigmoidal
También se pueden utilizar los «precomputed kernels» o kernels diseñados para propósitos específicos, pero el uso de este tipo de kernels se considera una forma avanzada de Machine Learning. De ese tema hablaremos después.
En el código que compartimos arriba podemos encontrar la siguiente instrucción:
|
1 |
clf = svm.SVC() |
En esta línea se construye una instancia de un clasificador SVM sin especificar un kernel. Cuando no se especifica una función kernel, la librería Sklearn asume que utilizaremos un kernel RBF. Si queremos especificar alguno de los 4 kernels antes mencionados, tendríamos que hacer lo siguiente:
|
1 2 3 4 |
clf = svm.SVC(kernel="linear") clf = svm.SVC(kernel="poly") clf = svm.SVC(kernel="rbf") clf = svm.SVC(kernel="sigmoid") |
Cualquiera de las tres opciones es válida. Cada una de ellas tendrá un performance distinto a las otras:
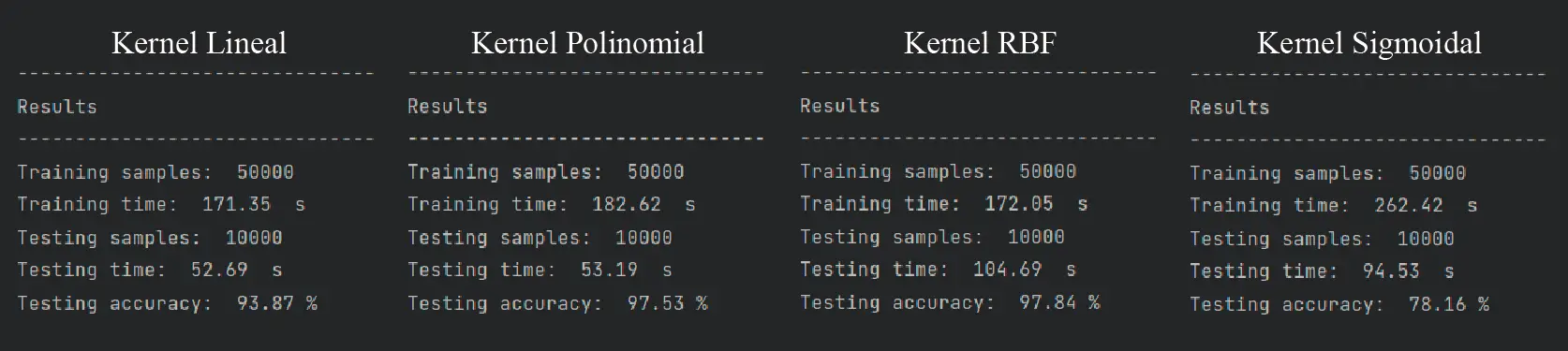
Como vemos, el mejor kernel de todos en cuanto a precisión en la clasificación es el RBF, el kernel por defecto del clasificador SVM. El kernel polinomial se acerca bastante en cuanto a la precisión, pero requiere de 10 segundos más para el entrenamiento. En la clasificación, sin embargo, el kernel polinomial clasifica las 10,000 imágenes del dataset de pruebas en la mitad del tiempo del kernel RBF.
Pero el tipo de kernel utilizado no es el único parámetro que se puede configurar. También está el «grado» de las función polinomial. Por defecto se utiliza un kernel polinomial cúbico, pero se puede cambiar a un cuadrático o de orden superior:
|
1 |
clf = svm.SVC(kernel="poly", degree=2) |
Con el kernel cuadrático obtuve un pequeño aumento en la precisión del algoritmo con kernel polinomial:
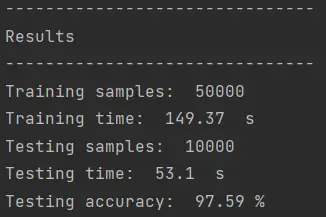
La diferencia fue de unas 6 imágenes con respecto al kernel cúbico. No es la gran cosa, pero un aumento es un aumento.
Hay otros parámetros que se pueden ajustar, como la variable gamma, la cantidad de iteraciones, el estado de aleatoreidad, entre otras. A continuación el listado de parámetros del clasificador SVM:
class sklearn.svm.SVC(*, C=1.0, kernel=‘rbf’, degree=3, gamma=‘scale’, coef0=0.0, shrinking=True, probability=False, tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1, decision_function_shape=‘ovr’, break_ties=False, random_state=None)
Con Sklearn es posible implementar un «barrido» de parámetros con el que se pueden probar distintas combinaciones de parámetros para mejorar el performance del clasificador, pero ese será un tema sobre el que escribiré un post exclusivo en los próximos días.
Por lo pronto creo que el concepto del algoritmo clasificador de imágenes ha quedado bien explicado. Para el lector de este post lo que sigue es hacer pruebas con el código para tratar de replicar lo que hice aquí como un primer paso en el fascinante mundo del Machine Learning.