Red Wine Quality dataset: ¿Regresión o Clasificación?

El vino ha sido una bebida apreciada durante milenios. La calidad del vino puede variar según muchos factores, tales como el tipo de uva, el proceso de fermentación, el almacenamiento, entre otros. Con el auge de la ciencia de datos, podemos utilizar datasets como el de la Calidad del Vino Tinto para obtener información sobre qué hace que un vino sea «bueno» o «malo».

En Kaggle podemos encontrar el Red Wine Quality dataset, el cual incluye datos relacionados con muestras del vino «Vinho Verde» en sus variante roja, del norte de Portugal. El objetivo es modelar la calidad del vino basado en pruebas fisicoquímicas.

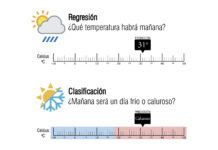
Este dataset le asigna un valor numérico a la calidad del vino, por lo cual se presta para ser utilizado con algoritmos de regresión y de clasificación. Es probable que el mejor approach sea la clasificación, pero en este post exploraremos ambas opciones para ver los contrastes entre cada tipo de algoritmo. Este post presentará la parte práctica de mi publicación anterior, ¿Cuál es la diferencia entre regresión y clasificación en Machine Learning?.

Por otro lado, estoy interesado en explorar distintos tipos de análisis sobre este dataset en el futuro, así que utilizaré este post como una introducción a mis lectores. Sin más que decir, comencemos.

Descripción del dataset

Como ya mencionamos, el dataset en cuestión contiene muestras de vino de la región Vinho Verde, ubicada en el noroeste de Portugal. Cada entrada en este conjunto de datos representa un vino específico, detallando tanto pruebas analíticas como sensoriales. Aquí hay algunas características clave del dataset:

• Composición del Dataset: Se organizó de manera que cada entrada denota una prueba específica, ya sea analítica o sensorial. El conjunto de datos final se exportó en un único archivo en formato CSV.
• Tipos de Vino: Debido a las diferencias en el sabor entre los vinos rojos y blancos, el análisis se realizó por separado. El dataset cuenta con 1,599 ejemplos de vino tinto.
• Estadísticas Fisicoquímicas: El estudio proporciona estadísticas detalladas para cada tipo de vino, incluyendo acidez fija, acidez volátil, ácido cítrico, azúcar residual, cloruros, dióxido de azufre libre y total, densidad, pH, sulfatos y contenido de alcohol. Cada atributo se presenta con valores mínimos, máximos y medios para ambos tipos de vinos.
• Evaluación Sensorial: Cada muestra de vino fue evaluada por al menos tres evaluadores sensoriales mediante catas a ciegas. Estos evaluadores calificaron el vino en una escala que va desde 0 (muy malo) hasta 10 (excelente). La puntuación sensorial final de cada vino se determina por la mediana de estas evaluaciones.

Este conjunto de datos proporciona una visión integral de las características fisicoquímicas de los vinos de la región Vinho Verde y de cómo estas características se correlacionan con las evaluaciones sensoriales realizadas por expertos en la materia.

Características (features) del dataset

A continuación les presento los features de este dataset:

1. Acidez Fija (Fixed Acidity): Mide la cantidad de ácidos totales presentes en el vino, que son fundamentales para la estabilidad y el sabor del vino.
2. Acidez Volátil (Volatile Acidity): Representa la cantidad de ácido acético en el vino, que en niveles altos puede llevar a un sabor desagradable similar al vinagre.
3. Ácido Cítrico (Citric Acid): Es uno de los ácidos principales presentes en el vino, que puede añadir frescura y sabor.
4. Azúcar Residual (Residual Sugar): Es la cantidad de azúcar que queda después de que finaliza la fermentación. Los vinos con mayor cantidad de azúcar residual son más dulces.
5. Cloruros (Chlorides): La cantidad de sal presente en el vino.
6. Dióxido de Azufre Libre (Free Sulfur Dioxide): Es la parte del dióxido de azufre que, al añadirse al vino, se combina con otras moléculas. Se utiliza para prevenir el crecimiento microbiano y la oxidación del vino.
7. Dióxido de Azufre Total (Total Sulfur Dioxide): Es la suma del dióxido de azufre libre y el que está unido a otras moléculas en el vino. Niveles altos pueden hacer que el vino tenga un sabor a quemado.
8. Densidad (Density): Relaciona la cantidad de materia en el vino con el volumen del mismo. Es un indicador de la concentración de compuestos en el vino.
9. pH: Mide la acidez o alcalinidad del vino en una escala de 0 (muy ácido) a 14 (muy alcalino). La mayoría de los vinos tienen un pH entre 3-4.
10. Sulfatos (Sulphates): Son sales o ácidos que contienen azufre. Pueden contribuir a los niveles de dióxido de azufre, que actúa como un antimicrobiano y antioxidante.
11. Alcohol: Representa el porcentaje de volumen de alcohol presente en el vino.
12. Calidad (Quality – variable de salida): Basada en datos sensoriales, es una puntuación entre 0 y 10 asignada por evaluadores sensoriales.

Estas características fisicoquímicas son esenciales para entender la composición del vino y cómo cada una de ellas puede influir en la calidad percibida del mismo.

Exploración del dataset

Desde este punto empezaré a presentar algunos gráficos e información que será procesada utilizando scripts en Python, los cuales se encuentran disponibles en nuestro repositorio de Machine Learning en Github.

En primer lugar, abrimos el archivo CSV con el dataset:

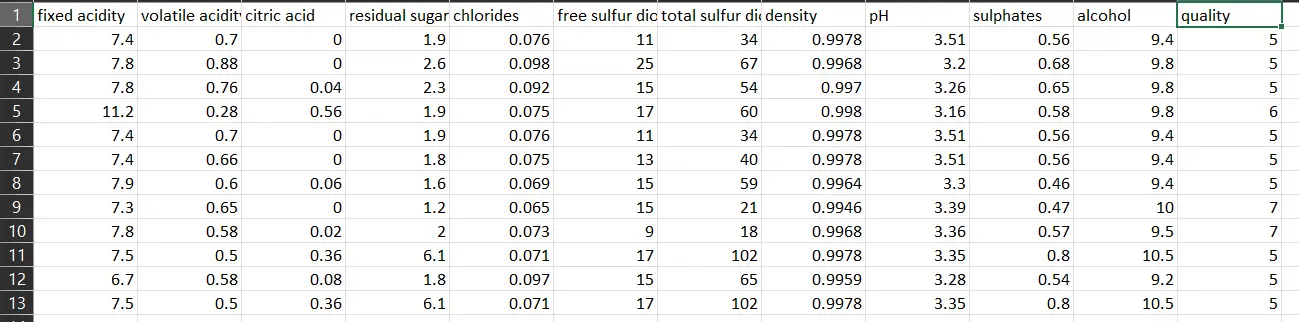
Como vemos, las primeras 11 columnas son features, y la doceava columna es la variable objetivo, la que trataremos de predecir. Como ya mencionamos anteriormente, el dataset cuenta con 1599 registros.

Ahora vamos a verificar la distribución de la variable objetivo, con tal de ver cuantas muestras de cada tipo de vino contiene el dataset. Eso lo podemos lograr con este código:

Este script lo pueden encontrar en nuestro repositorio de Github, y produce el siguiente resultado:

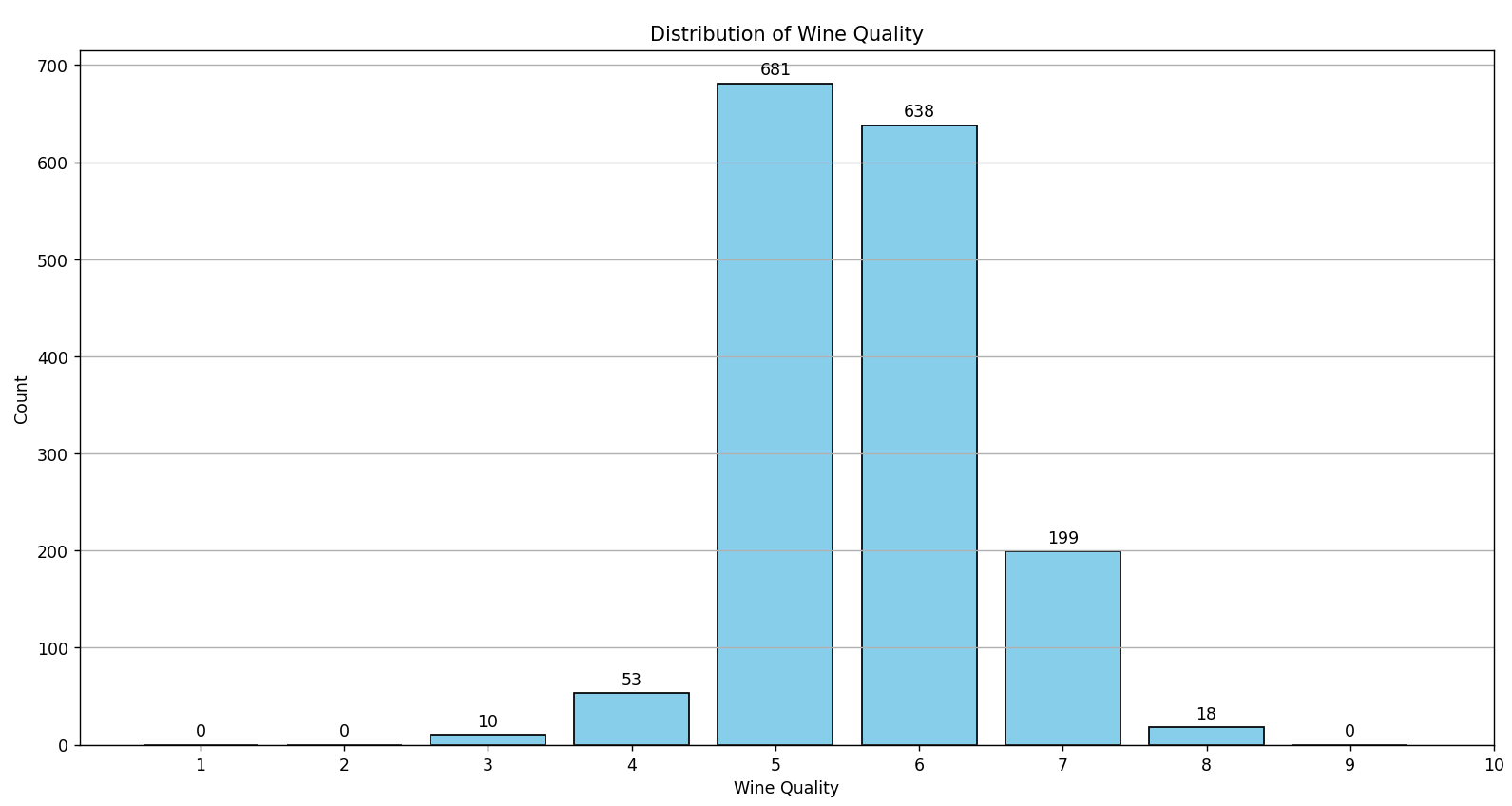
Como se observa en la gráfica, no existen vinos categorizados con los valores 0, 1, 2, 9 o 10. La clasificación de los vinos se concentra entre los valores 3 y 8, con la mayoría (aproximadamente el 82%) clasificados entre 5 y 6. Este predominio en ciertas categorías de calidad puede complicar el entrenamiento de algoritmos de clasificación.

Un modelo de Machine Learning podría desarrollar un sesgo hacia estas clases dominantes, prediciendo frecuentemente estas simplemente por ser las más comunes en el conjunto de datos. Este desequilibrio no solo sesga al modelo, sino que también puede resultar en métricas de rendimiento engañosas. Un alto porcentaje de precisión podría simplemente reflejar la predicción correcta de la clase mayoritaria, dejando a las clases minoritarias mal reconocidas o incluso ignoradas.

Debido a esto, es posible que los algoritmos de regresión podrían ser más adecuados para el desarrollo de un modelo predictivo para este dataset. La razón es que, en lugar de intentar clasificar el vino en categorías discretas, un algoritmo de regresión intentaría predecir un valor continuo para la calidad del vino. Esto permite una mayor flexibilidad y precisión en las predicciones, ya que no se limita a categorías fijas (clases). Además, al tratar la calidad del vino como un espectro continuo en lugar de categorías discretas, se evita el problema del desequilibrio de clases y se obtiene una representación más matizada de la calidad del vino.

Ahora utilizaremos un script similar al anterior para graficar la distribución de los features:

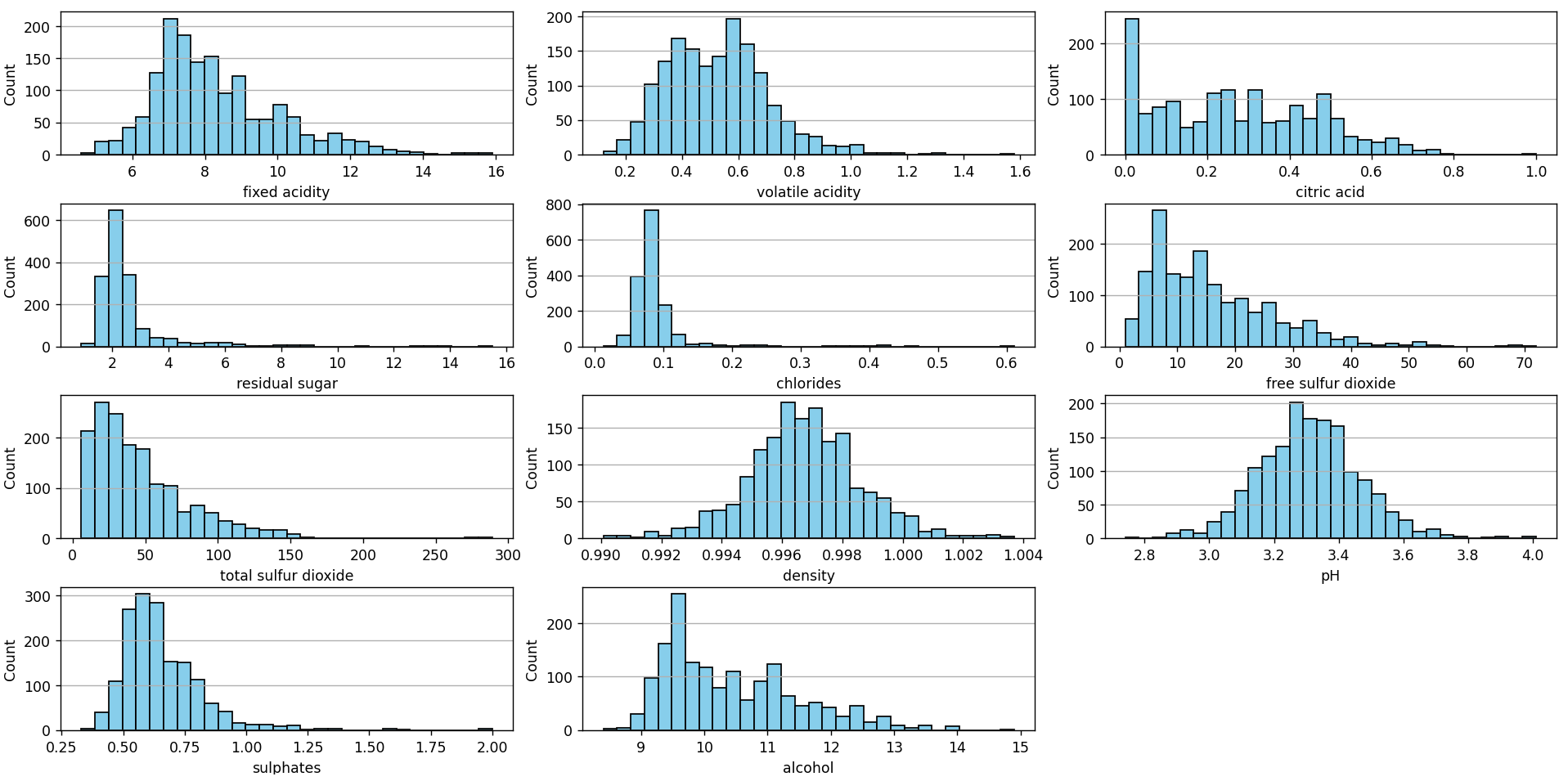
Al observar los histogramas de cada uno de los features, podemos discernir la distribución y tendencia central de los datos para cada característica, identificando si se asemejan a una distribución normal o si presentan asimetrías hacia la izquierda o derecha. Estos histogramas también revelan la dispersión y rango de valores, permitiendo identificar posibles valores atípicos o concentraciones de datos. Además, múltiples picos en un histograma pueden indicar la presencia de subgrupos o modas dentro de una característica.

En conjunto, estos histogramas ofrecen una visión panorámica de la estructura y variabilidad de cada característica en el dataset.

Otro análisis interesante es la matriz de correlación. Esta matrix la podemos construir con este script, disponible en nuestro repositorio.

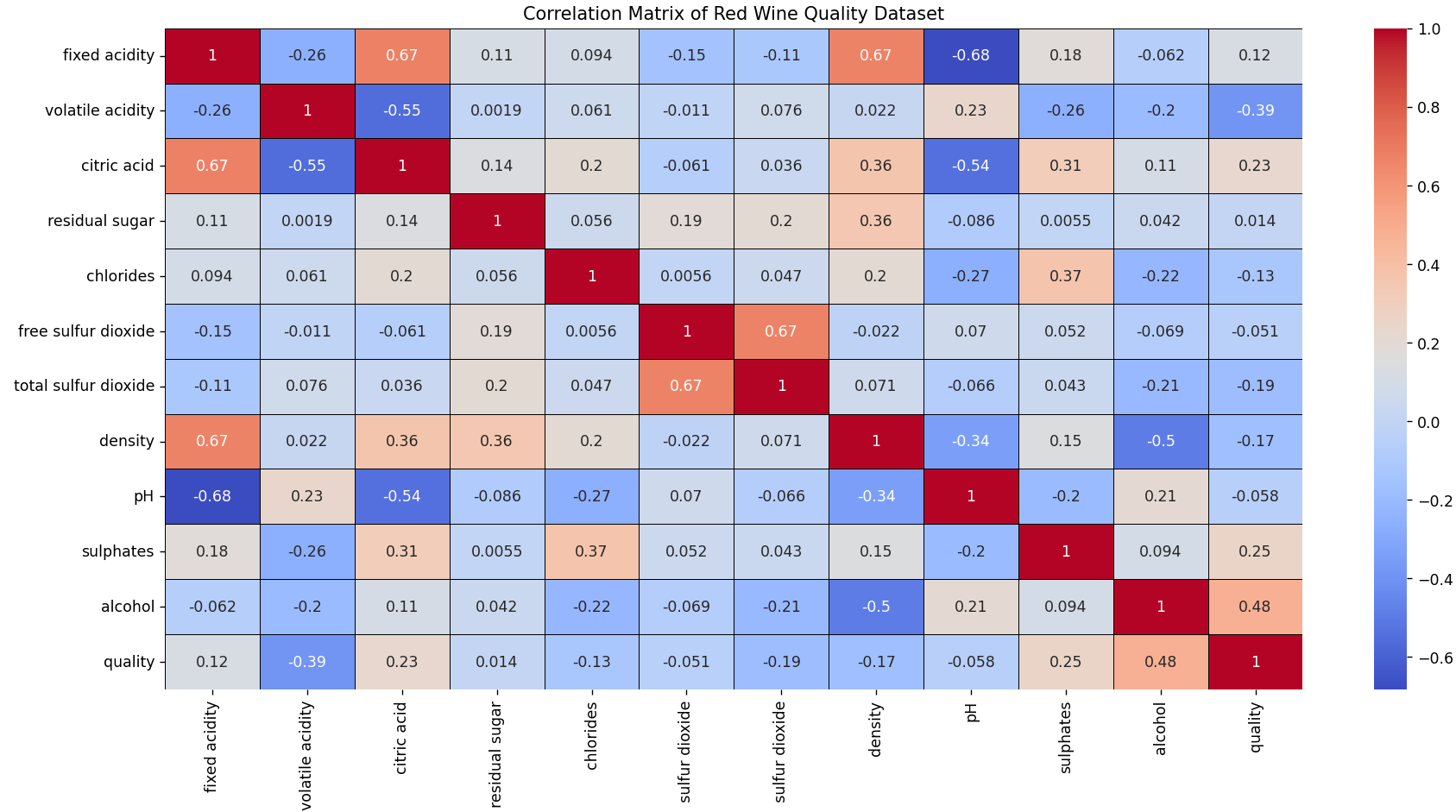
Esta matriz muestra la correlación entre las variables, donde los colores más intensos representan una correlación más fuerte.

Correlaciones Fuertes

Correlaciones Positivas

• • • La acidez fija está positivamente correlacionada con el ácido cítrico y la densidad.
    • Existe una fuerte relación positiva entre el dióxido de azufre libre y el dióxido de azufre total.

Correlaciones Negativas

• • • Existe una relación negativa entre la acidez fija y el pH.
    • El ácido cítrico está negativamente correlacionado con el pH.
    • El contenido de alcohol está negativamente asociado con la densidad.

Correlaciones Moderadas

• • Hay una relación positiva moderada entre el ácido cítrico y los sulfatos.
  • Los cloruros y los sulfatos están moderadamente correlacionados.
  • Los vinos con mayor contenido de alcohol tienden a tener mejores calificaciones de calidad.
  • Una mayor acidez volátil está asociada con una menor calidad del vino.

Observaciones Notables

• La calidad del vino está influenciada positivamente por su contenido de alcohol y negativamente por su acidez volátil.
• Como se esperaría por la naturaleza de las variables, la acidez y el pH están inversamente relacionados.

Implicaciones para el modelado

• Si se construye un modelo predictivo, hay que tener cuidado al usar variables que estén altamente correlacionadas juntas, ya que pueden llevar a problemas de multicolinealidad.
• Las variables más correlacionadas con la calidad podrían ser predictores importantes si se modela la calidad del vino.

Otra técnica de análisis que se suele utilizar como parte del pre-procesamiento de datos es la representación gráfica de los datos a través del Análisis de Componentes Principales (PCA, por sus siglas en inglés). El PCA es un método estadístico que transforma las variables originales, posiblemente correlacionadas, en un nuevo conjunto de variables descorrelacionadas llamadas componentes principales. Estos componentes son ortogonales entre sí y capturan la varianza del conjunto de datos en orden descendente.

El primer componente principal captura la mayor varianza posible del conjunto de datos, mientras que cada componente subsiguiente captura la máxima varianza restante, bajo la restricción de que es ortogonal a los componentes anteriores. Esto permite reducir la dimensionalidad del conjunto de datos, conservando al mismo tiempo la máxima cantidad de información.

En el contexto de la visualización, el PCA es especialmente útil porque nos permite representar conjuntos de datos de alta dimensionalidad en un espacio bidimensional o tridimensional, facilitando la identificación de patrones, agrupaciones o posibles outliers en los datos. Estas visualizaciones pueden revelar estructuras subyacentes, relaciones entre grupos o la variabilidad dentro del conjunto de datos, que de otro modo serían difíciles de discernir en un espacio de alta dimensión.

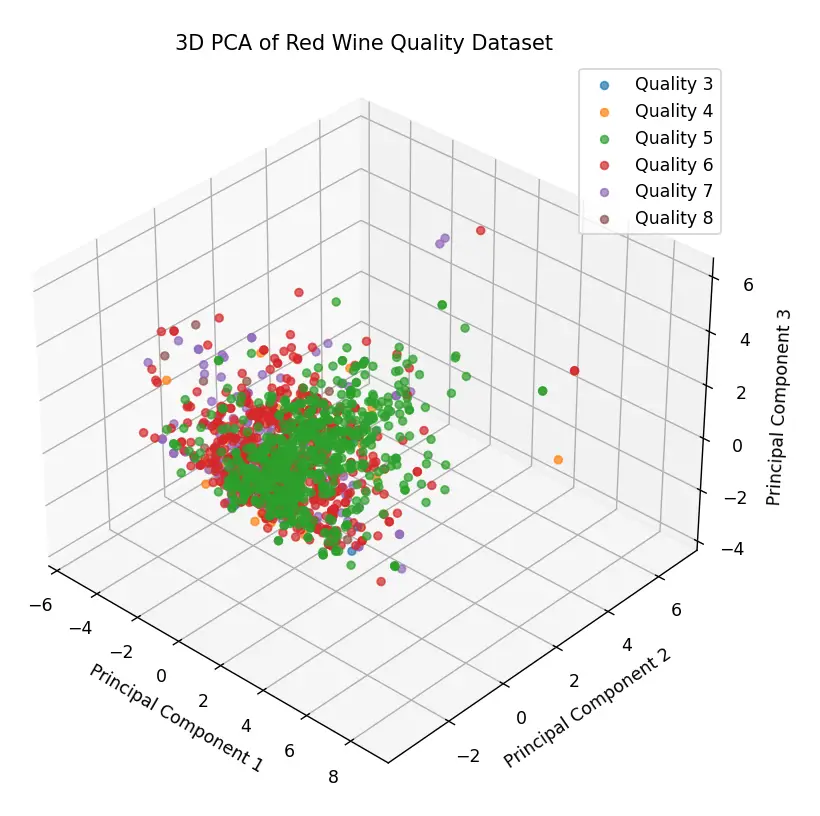
El gráfico tridimensional que se muestra a continuación fue generado mediante el uso de PCA (Análisis de Componentes Principales) y se puede encontrar el código fuente en este enlace. En esta representación, cada punto corresponde a un vino específico y sus coordenadas reflejan sus características fisicoquímicas. El color de los puntos indica la calidad del vino: por ejemplo, los puntos rojos representan vinos con una calificación de calidad de 6.

Esta visualización revela varias características interesantes del dataset. En primer lugar, hay una aglomeración notable de puntos, lo que sugiere que muchas muestras de vino tienen características fisicoquímicas similares. Esta agrupación densa podría indicar que la mayoría de los vinos en este dataset comparten ciertas propiedades fisicoquímicas.

Sin embargo, también se observan algunos puntos que se desvían significativamente del grupo principal, los cuales podríamos considerar como outliers. Estos valores atípicos son importantes de señalar, ya que pueden afectar la eficiencia y precisión de un modelo de aprendizaje automático. Dependiendo del objetivo y del tipo de modelo a entrenar, es posible que sea necesario abordar estos valores atípicos mediante técnicas de preprocesamiento o considerarlos en el análisis posterior.

Sin embargo, por ahora, nos centraremos en el objetivo principal de este post: evaluar algoritmos de clasificación y regresión en este conjunto de datos.

Predicciones con algoritmos de Regresión

Para determinar el algoritmo más adecuado, emplearé un método que se apoya en la función all_estimators de Scikit-Learn. Esta función nos permite acceder a una amplia gama de algoritmos de regresión, abarcando entre 30 y 40 distintos modelos.

En lugar de evaluar cada modelo de manera individual, el método que propongo realiza una validación cruzada 10-fold (10-kfold) de cada uno de ellos de manera automática, comparando su rendimiento en el conjunto de datos proporcionado. Esta técnica de 10-kfold asegura que cada muestra se use una vez como validación mientras las 9 restantes forman parte del conjunto de entrenamiento.

Para medir la precisión de cada modelo, se utiliza el RMSE (Root Mean Squared Error) como métrica de evaluación. Al hacerlo, se elimina el tedioso proceso manual de selección y se agiliza la identificación del modelo de regresión más prometedor para el dataset en cuestión, basándose en el valor de RMSE obtenido. Es una estrategia que combina precisión y eficiencia en el proceso de elección del modelo.

El script es el siguiente:

Este script está disponible aquí. El resultado de ejecutar este código sobre este dataset lo presento en la siguiente tabla:

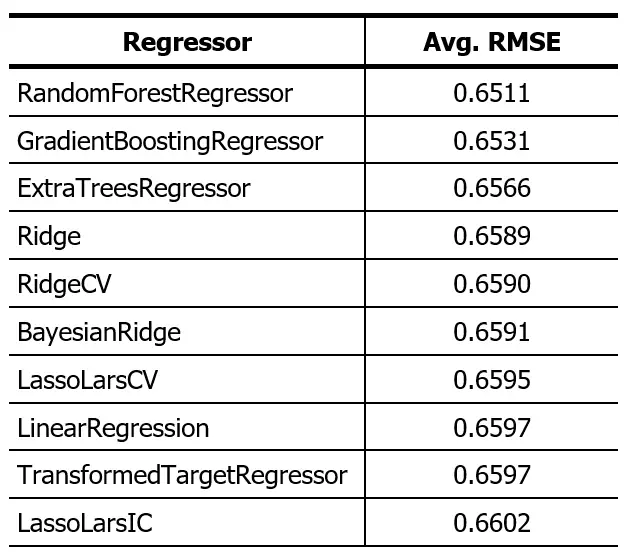
El algoritmo «Random Forest Regressor» ha demostrado tener el rendimiento más destacado. Sin embargo, es relevante señalar que la discrepancia en el desempeño entre los cinco algoritmos principales es mínima. Con este resultado en mente, procederemos a emplear el «Random Forest Regressor». Dividiremos el dataset siguiendo una proporción de 80:20 y observaremos cómo el algoritmo realiza predicciones sobre el 20% de datos reservados para pruebas.

El script es el siguiente:

Este script, disponible aquí, produce el siguiente resultado:

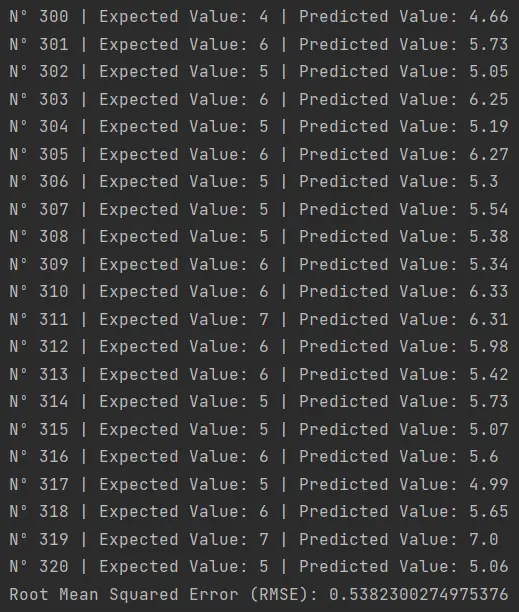
Aquí es donde podemos apreciar las fortalezas y limitaciones de utilizar un algoritmo de regresión. Aunque el algoritmo nos brinda una salida con valores decimales, no siempre acierta con precisión el valor exacto que se espera. Por ejemplo:

• En la muestra 316, la predicción fue de 5.6 cuando el valor real era 6.
• En la muestra 317, se predijo 4.99 cuando debió ser 5.
• En la muestra 320, la estimación fue de 5.06, siendo el valor real 5.

Una solución práctica a este desafío podría ser redondear las predicciones a números enteros. De esta forma, podemos mitigar ciertos errores y evaluar con mayor claridad la eficacia del algoritmo en sus predicciones.

Este script integra el redondeo de las predicciones del regresor. El resultado no luce muy bien:

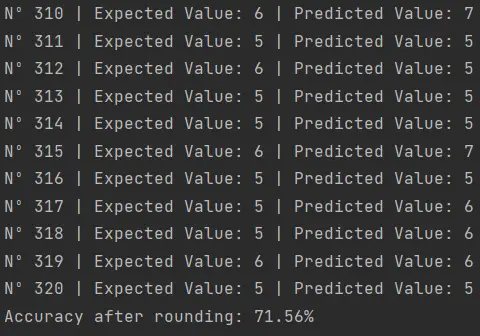
Una precisión del 71.56% es un resultado moderado en el ámbito del Machine Learning. Existen múltiples estrategias y ajustes que podríamos implementar para optimizar y elevar esta cifra.

Volveré a ejecutar el script que selecciona algoritmos de regresión, pero en esta ocasión redondearé el resultado y evaluaré el rendimiento de cada algoritmo como si fuesen algoritmos de clasificación. Utilizaré este script.

El resultado obtenido fue:

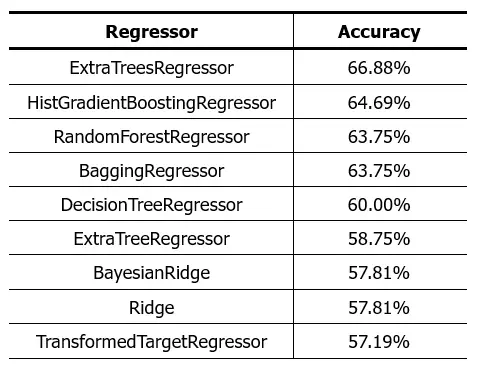
Como vemos, los resultados no lucen muy prometedores. La diferencia en la precisión del Random Forest que probamos anteriormente se debe a que para el 10-fold cross validation se utiliza una proporción 9:1 y en la prueba anterior utilizamos 8:2.

Enteoría el ExtraTreesRegressor debe darnos un mejor resultado que el 71.56% del Random Forest, pero no espero que la diferencia sea mucha. Todo parece indicar que los algoritmos de regresión no son buenos para ser utilizados como modelos predictivos en este dataset, o que nos hace falta utilizar técnicas más avanzadas de procesamiento de datos para lograr mejores resultados.

Predicciones con algoritmos de Clasificación

Ahora exploraremos la utilización de algoritmos de clasificación en el conjunto de datos de calidad del vino tinto. Dado que la calidad del vino en el conjunto de datos es una variable discreta (categorizada del 3 al 8), es lógico pensar que un algoritmo de clasificación puede ser adecuado para este problema. Aunque anteriormente mencionamos que el desequilibrio en las clases puede ser un desafío, intentaremos utilizar los algoritmos de clasificación para ver qué tan bien se desempeñan en comparación con los algoritmos de regresión.

Al igual que lo hicimos con los algoritmos de regresión, utilizaremos la función all_estimators de Scikit-Learn para obtener una lista de todos los algoritmos de clasificación disponibles. Luego, aplicaremos una validación cruzada 10-fold en cada uno de ellos para evaluar su rendimiento en el conjunto de datos.

El script utilizado para este propósito nos produjo el siguiente resultado:

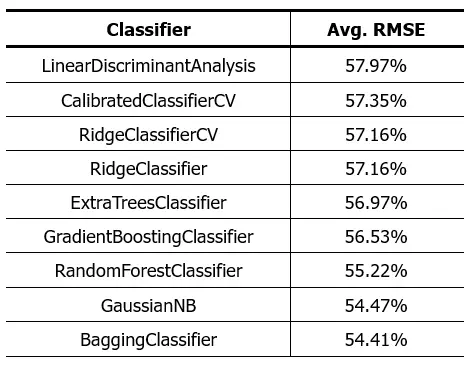
Como vemos los resultados no son mejores que los obtenidos con los algoritmos de regresión. Esto nos lleva a reconsiderar algunas suposiciones que podríamos haber tenido al inicio de este análisis. Es posible que el problema de predicción de la calidad del vino no se adecue tan bien a un enfoque estrictamente de clasificación o regresión utilizando las características fisicoquímicas del vino como variables de entrada.

Como vimos en la representación tridimensional de los datos, los datos están estrechamente entrelazados y no es posible diferenciar las distintas clases del dataset. Hará falta realizar un análisis más profundo para encontrar un algoritmo que logre mejores resultados en este dataset.

Posibles Explicaciones y Estrategias a Considerar

1. Características del dataset: Aunque hemos trabajado con diversas características fisicoquímicas del vino, es posible que la calidad del vino esté influenciada por otros factores no contemplados en este conjunto de datos, como las condiciones de crecimiento de las uvas, la técnica de producción, entre otros.
2. Desequilibrio de Clases: Como se mencionó anteriormente, la mayoría de las muestras de vino se clasifican entre 5 y 6. Un conjunto de datos desequilibrado puede llevar a modelos que están sesgados hacia las clases dominantes. Podríamos considerar técnicas de reequilibrio, como el oversampling de clases minoritarias o el undersampling de clases mayoritarias.
3. Características derivadas: Es posible que necesitemos crear nuevas características a partir de las existentes o incluso combinar algunas para obtener una representación más significativa del dataset.
4. Enfoques Híbridos: Podríamos considerar combinar algoritmos de clasificación y regresión o incluso emplear técnicas de aprendizaje profundo (Deep Learning) para abordar el problema desde una perspectiva diferente.
5. Correlación de los Datos: Una revisión exhaustiva de la correlación entre las características puede ser esencial. Las características altamente correlacionadas pueden llevar a problemas de multicolinealidad en modelos lineales. Es crucial entender estas correlaciones para determinar si estamos introduciendo nueva información o redundancia en el modelo.

Próximos Pasos

A la luz de estos resultados, hay varias estrategias que podríamos considerar para mejorar el rendimiento de nuestros modelos:

1. Realizar un análisis más profundo de las características para identificar y posiblemente eliminar aquellas que no contribuyen significativamente a la predicción de la calidad del vino.
2. Experimentar con técnicas de ingeniería de características (feature engineering) para crear nuevas características que puedan ser más informativas.
3. Utilizar técnicas de regularización para prevenir el overfitting y mejorar la generalización del modelo en datos no vistos.
4. Considerar la utilización de redes neuronales y Deep Learning, que podrían ser capaces de capturar patrones más complejos en los datos.

Conclusión

En este post hemos analizado en detalle el Red Wine Quality Dataset, que presenta las características fisicoquímicas de una variedad específica de vino y su relación con la calidad del mismo.

A pesar de los esfuerzos realizados y de las técnicas aplicadas, los algoritmos de clasificación y regresión actuales no han mostrado un rendimiento óptimo. Esto puede deberse a diversos factores, desde la naturaleza entrelazada de los datos, pasando por posibles desequilibrios en las clases, hasta la correlación entre las características. Sin embargo, es importante recordar que cada conjunto de datos presenta desafíos únicos y, a menudo, requiere un enfoque personalizado para extraer la información más valiosa.

Como científicos de datos, nuestra misión no se detiene ante los obstáculos. En entregas futuras, nos embarcaremos en una exploración más profunda, presentando y probando diferentes técnicas y enfoques con este dataset. Nuestro objetivo es mejorar el rendimiento de los algoritmos y, en el proceso, brindar a la comunidad herramientas y conocimientos que puedan ser aplicados en contextos similares.

La ciencia de datos es un viaje de constante aprendizaje y adaptación, y esperamos que nos acompañen en nuestras próximas entregas sobre este tema.