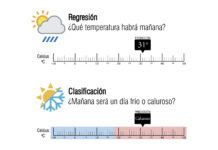
El Deep Learning es una rama de la Inteligencia Artificial que se ha vuelto cada vez más popular en los últimos años debido a sus impresionantes capacidades para resolver problemas complejos de manera eficiente.
Uno de los problemas más comunes en el Deep Learning es la clasificación de imágenes, que implica asignar una etiqueta o categoría a una imagen dada. En este tutorial, aprenderás cómo utilizar PyTorch, una de las bibliotecas de Deep Learning más populares y de más rápido crecimiento, para entrenar una red neuronal completamente conectada (fully connected neural network) para la clasificación de imágenes utilizando el conjunto de datos MNIST.
El conjunto de datos MNIST es un conjunto de datos ampliamente utilizado que contiene imágenes de dígitos escritos a mano del 0 al 9. Sobre este dataset ya hemos escrito bastante aquí en Panama Hitek.
En este post aprenderás cómo cargar los datos, construir la red neuronal, entrenarla y evaluar su rendimiento. Al final de este tutorial, tendrás una comprensión sólida de cómo construir y entrenar una red neuronal simple para la clasificación de imágenes utilizando PyTorch y MNIST.
Sin más que decir, comencemos.
Redes Neuronales en Pytorch
PyTorch es una de las bibliotecas de Deep Learning más populares y de más rápido crecimiento. Fue desarrollada por Facebook AI Research y se basa en Torch, que es una biblioteca de Deep Learning de código abierto. PyTorch proporciona herramientas para construir y entrenar redes neuronales de manera eficiente y se ha convertido en una de las herramientas preferidas por los investigadores y desarrolladores de Deep Learning.
En PyTorch, las redes neuronales se definen utilizando la clase nn.Module. Cada red neuronal se define como una subclase de nn.Module, y se pueden agregar capas y otros módulos de PyTorch como atributos de la clase. Una vez que se define la arquitectura de la red neuronal, se puede entrenar utilizando las funciones de pérdida y optimización proporcionadas por PyTorch.
PyTorch también proporciona herramientas para trabajar con datos de manera eficiente, como la clase DataLoader, que se utiliza para cargar datos de entrenamiento y prueba en lotes. Además, PyTorch es compatible con la GPU, lo que permite acelerar significativamente el proceso de entrenamiento y evaluación de la red neuronal.
La red neuronal que vamos a utilizar en este post es una red neuronal completamente conectada (fully connected neural network) con una arquitectura simple. La red neuronal consta de dos capas completamente conectadas (fully connected layers), donde la primera capa tiene 784 entradas (ya que las imágenes de MNIST son de 28×28 píxeles) y 128 salidas, y la segunda capa tiene 128 entradas y 10 salidas (una para cada dígito del 0 al 9). La función de activación utilizada es ReLU (Rectified Linear Unit), que es una de las funciones de activación más utilizadas en las redes neuronales.
La siguiente imagen muestra una representación visual de la red neuronal que utilizaremos en este post:
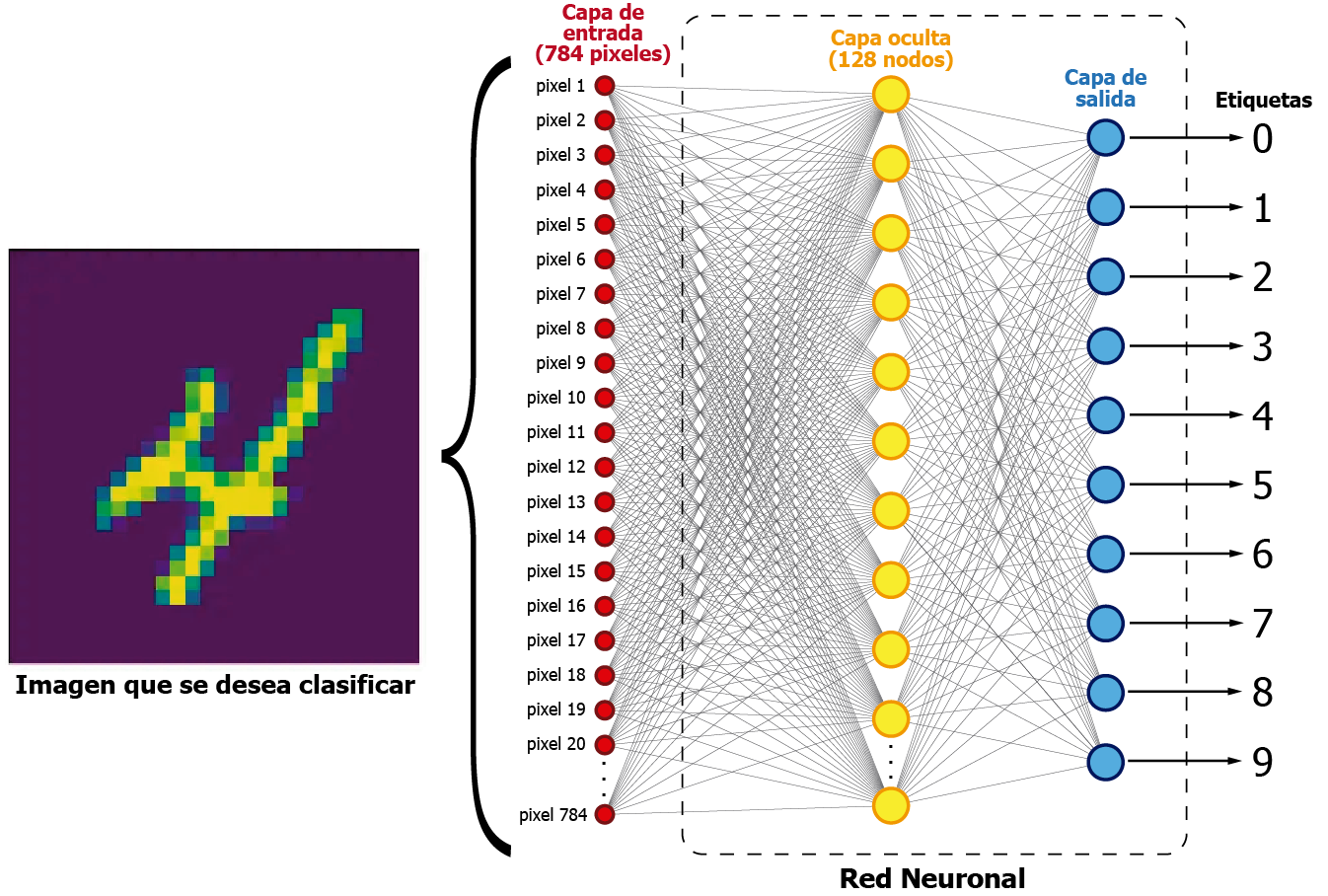
Las imágenes del MNIST dataset tienen una dimensión de 28×28 pixeles. El resultado de esa multiplicación es 784. La red neuronal aquí presentada utiliza esos 784 pixeles como datos de entrada. Internamente tiene 128 nodos en la capa oculta, los cuales unen la entrada y la salida de la red neuronal.
Por cada imagen, la red tratará de interpretar los pixeles de cada muestra y «aprenderá» a asignarle una probabilidad en la capa de salida. De esta manera, el nodo de salida (azul) con la probabilidad más alta será el que nos indique cual de los 10 números estamos procesando en un momento dado. Este es un concepto básico sobre redes neuronales, así que no ahondaré mucho en este tema.
El siguiente código presenta una implementación en Python utilizando Pytorch para crear una red neuronal de 784 entradas, 128 nodos en la capa oculta y 10 nodos en la capa de salida. El código se encuentra disponible en nuestro repositorio de Github:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 |
# Import necessary libraries import pandas as pd import numpy as np import time as time import torch import torch.nn as nn import torch.optim as optim from torch.utils.data import DataLoader, TensorDataset # Define the number of training and testing samples trainingSamples = 50000 testingSamples = 10000 """ Set global variables for the computing time of both training and testing """ startTrainingTime = 0 endTrainingTime = 0 trainingTime = 0 startTestingTime = 0 endTestingTime = 0 testingTime = 0 # Function for loading data from a CSV file and returning the data and labels def loadDataset(fileName, samples): x = [] # Array for data inputs y = [] # Array for labels (expected outputs) # Load data from a CSV file and store it in a pandas DataFrame object with open(fileName, 'r') as f: train_data = pd.read_csv(f) # Extract labels from the first column of the DataFrame object y = np.array(train_data.iloc[0:samples, 0]) # Extract data from the remaining columns of the DataFrame object and normalize it x = np.array(train_data.iloc[0:samples, 1:]) / 255 # Convert the data and labels to PyTorch tensors x = torch.tensor(x, dtype=torch.float32) y = torch.tensor(y, dtype=torch.long) # Return the data and labels return x, y # Define a simple neural network class class SimpleNeuralNetwork(nn.Module): def __init__(self): super(SimpleNeuralNetwork, self).__init__() # Define a fully connected layer with 784 input features (28x28 images) and 128 output features self.fc1 = nn.Linear(784, 128) # Define a fully connected layer with 128 input features and 10 output features (for the 10 digits) self.fc2 = nn.Linear(128, 10) # Define the activation function as ReLU self.activation = nn.ReLU() def forward(self, x): # Flatten the input image into a 1D vector x = x.view(-1, 784) # Pass the input through the first fully connected layer and apply the activation function x = self.fc1(x) x = self.activation(x) # Pass the output of the first layer through the second fully connected layer x = self.fc2(x) # Return the output return x # Main function def main(): # Load the training and testing datasets train_x, train_y = loadDataset("../../../../datasets/mnist/mnist_train.csv", trainingSamples) test_x, test_y = loadDataset("../../../../datasets/mnist/mnist_test.csv", testingSamples) # Define the batch size for training and testing data batchSize = 64 # Define a DataLoader object for the training data train_loader = DataLoader(TensorDataset(train_x, train_y), batch_size=batchSize, shuffle=True) # Define a DataLoader object for the testing data test_loader = DataLoader(TensorDataset(test_x, test_y), batch_size=batchSize) device = torch.device("cpu") # remove to use GPU, is available # Create a SimpleNeuralNetwork object and define the loss function and optimizer model = SimpleNeuralNetwork().to(device) loss_function = nn.CrossEntropyLoss() optimizer = optim.Adam(model.parameters()) # Train the model and measure the time startTrainingTime = time.time() # Set the number of epochs for training epochs = 20 # Loop over the specified number of epochs for epoch in range(epochs): epoch_loss = 0.0 epoch_accuracy = 0.0 # Loop over the batches of training data for i, data in enumerate(train_loader): inputs, labels = data # Zero the gradients of the model parameters optimizer.zero_grad() # Forward pass through the model outputs = model(inputs) # Calculate the loss loss = loss_function(outputs, labels) # Backward pass through the model and update the parameters loss.backward() optimizer.step() # Update the epoch loss and accuracy epoch_loss += loss.item() _, predicted = torch.max(outputs.data, 1) correct = (predicted == labels).sum().item() epoch_accuracy += correct / batchSize # Print out the epoch loss and accuracy print("Epoch:", epoch + 1, " Loss:", epoch_loss / len(train_loader), " Accuracy:", epoch_accuracy / len(train_loader)) endTrainingTime = time.time() trainingTime = endTrainingTime - startTrainingTime # Evaluate the model on the testing data and measure the time validResults = 0 startTestingTime = time.time() for i in range(len(test_y)): inputs = test_x[i].unsqueeze(0) labels = torch.tensor([test_y[i]], dtype=torch.long) # Forward pass through the model outputs = model(inputs) _, predicted = torch.max(outputs.data, 1) result = predicted.item() expectedResult = int(labels[0]) outcome = "Fail" if result == expectedResult: validResults = validResults + 1 outcome = " OK " print("Nº ", i + 1, " | Expected result: ", expectedResult, " | Obtained result: ", result, " | ", outcome, " | Accuracy: ", round((validResults / (i + 1)) * 100, 2), "%") endTestingTime = time.time() testingTime = endTestingTime - startTestingTime # Calculate and print out the training and testing time and the testing accuracy print("-------------------------------") print("Results") print("-------------------------------") print("Training samples: ", trainingSamples) print("Training time: ", round(trainingTime, 2), " s") print("Testing samples: ", testingSamples) print("Testing time: ", round(testingTime, 2), " s") print("Testing accuracy: ", round((validResults / testingSamples) * 100, 2), "%") # Run the main function if this file is being executed directly if __name__ == "__main__": main() |
La red neuronal implementada en este código utiliza un algoritmo de aprendizaje supervisado conocido como backpropagation para actualizar los pesos de la red neuronal en cada iteración durante el entrenamiento.
En cada iteración, se alimenta la red neuronal con un lote de imágenes y se calcula la pérdida entre las etiquetas esperadas y las predicciones realizadas por la red. Luego, el algoritmo de backpropagation propaga el error hacia atrás en la red y ajusta los pesos de las neuronas para reducir la pérdida.
Este proceso se repite varias veces hasta que la red neuronal ha alcanzado una precisión aceptable en la clasificación de las imágenes. Una vez entrenada, la red se utiliza para predecir las etiquetas de las imágenes de prueba y se calcula su precisión de clasificación.
El resultado de ejecutar este código es el siguiente:
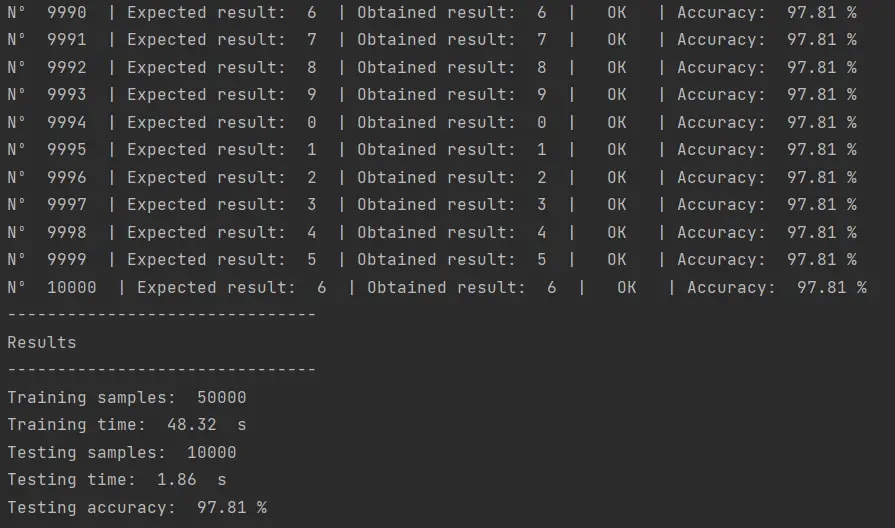
Como vemos, hemos logrado un 97.81% de eficiencia en la clasificación de imágenes. Esto quiere decir que de las 10,000 imágenes que intentamos clasificar, hemos logrado estimar el número representado en la imagen en 9781 imágenes.
Este resultado es muy bueno. Aquí en Panama Hitek hemos probado múltiples algoritmos de clasificación en MNIST y este resultado es la tercera eficiencia más alta, justo por debajo de una red neuronal similar a esta en Tensorflow y el Support Vector Machine:
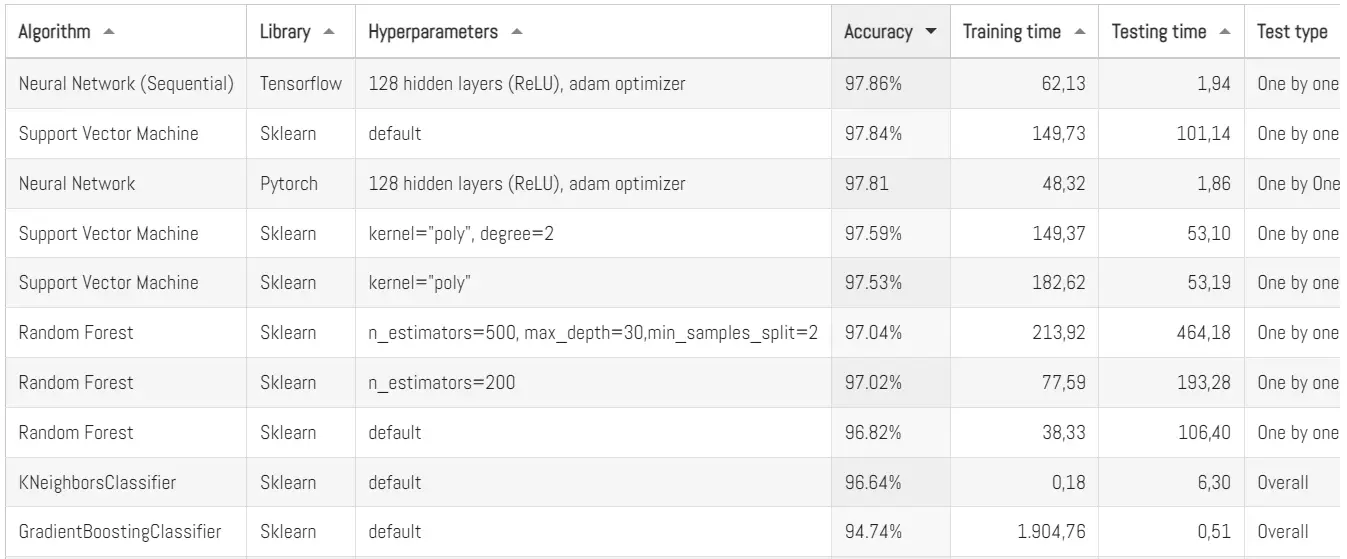
Como vemos, el algoritmo aquí presentado es ligeramente menos eficiente que otros, pero también requiere de un menor tiempo de entrenamiento y menor tiempo de pruebas. Y eso sin contar que en este post solamente estoy usando CPU.
Si se quiere utilizar GPU, hace falta modificar estas líneas del código:
|
1 2 |
device = torch.device("cpu") model = SimpleNeuralNetwork().to(device) |
Esas dos líneas deben remplazarse por:
|
1 |
model = SimpleNeuralNetwork() |
De esta forma el algoritmo utilizará GPU, en caso de que la computadora que se esté utilizando cuente con el hardware para esto. Sobre este tema escribiré un post más adelante en el que espero comparar el performance de CPU vs GPU en algoritmos de Machine Learning.
Probando el algoritmo con mi escritura
Los que siguen mis publicaciones en este blog saben que cada vez que pruebo un algoritmo de Machine Learning con MNIST me gusta hacerlo también con mi números manuscritos. Hace unos meses escribí un post sobre este tema.
Mi dataset de imágenes luce así:

Vamos a ver como le va a la red neuronal en Pytorch con estos números. Hasta ahora no he encontrado ningún algoritmo que logre clasificar todos estos números de manera correcta.
El script utilizado para probar la red neuronal con mis números se encuentra disponible en nuestro repositorio de Github y produce el siguiente resultado:
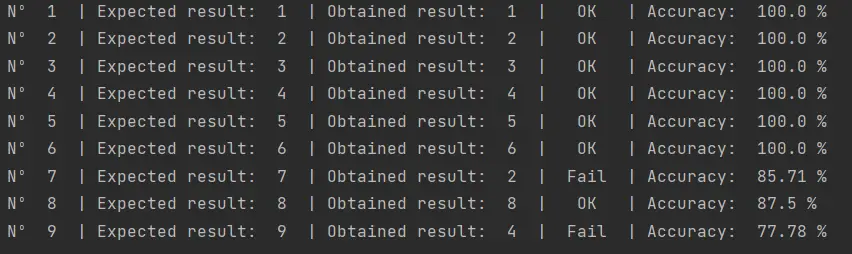
Como vemos aún no logramos clasificar correctamente los números de mi escritura. Supongo que tendré que analizar este problema de manera más profunda en otro post.
Conclusiones
En conclusión, hemos presentado una implementación básica de un algoritmo en Pytorch de aprendizaje automático supervisado utilizando el método de regresión logística. A través de este ejercicio, hemos demostrado cómo se puede entrenar un modelo para predecir una variable binaria a partir de un conjunto de datos de entrenamiento. Además, hemos explorado algunos conceptos clave en el aprendizaje automático, como la función de coste y la regularización, y cómo estos afectan el rendimiento del modelo.
Es importante destacar que, si bien el modelo obtenido tuvo una precisión aceptable, se podría mejorar su rendimiento a través de la optimización de hiperparámetros. Es decir, ajustando los diferentes parámetros del modelo, como el valor de lambda en la regularización o el número de iteraciones en el algoritmo de optimización, podríamos obtener un modelo más preciso y robusto.
En futuros posts, abordaremos estos temas en mayor detalle y exploraremos otras técnicas de aprendizaje automático para problemas de clasificación y regresión. También exploraremos cómo lidiar con conjuntos de datos desbalanceados y cómo evaluar el rendimiento del modelo de manera adecuada.
Finalmente, quiero agradecer al lector por tomarse el tiempo de leer este post y espero que haya encontrado útil esta introducción al aprendizaje automático y a la regresión logística. Si tiene alguna pregunta o comentario, no dude en dejarlos abajo. Estaré encantado de responder y discutir cualquier inquietud que pueda tener.