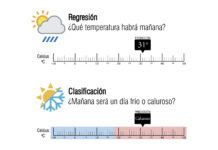
El clasificador K-Nearest Neighbors (KNN) es un método sencillo y efectivo para la clasificación de imágenes. En este artículo, exploraremos el uso del clasificador KNN en el conocido conjunto de datos MNIST de dígitos escritos a mano.
Usaremos la librería scikit-learn en Python para entrenar y evaluar el clasificador y realizaremos una búsqueda de hiperparámetros para encontrar la mejor combinación de parámetros para el modelo KNN. Al final de este artículo, entenderás cómo usar el clasificador KNN para la clasificación de imágenes y cómo optimizar su rendimiento a través del ajuste de hiperparámetros.
Características del clasificador K-Nearest Neighbor
El algoritmo K-Nearest Neighbors es un método de clasificación no paramétrico que asigna a una muestra una clase basándose en la mayoría de las clases de sus vecinos más cercanos en el espacio de características. En otras palabras, una muestra se clasifica según la clase más común de las K muestras más cercanas a ella en el espacio de características. KNN es comúnmente utilizado en problemas de clasificación y regresión.
El valor de k se determina por el usuario y puede afectar la complejidad y la precisión del modelo. El parámetro «k» es el número de vecinos más cercanos que se utilizan para hacer una predicción. Por ejemplo, si k=3, entonces el algoritmo considerará a los 3 vecinos más cercanos a una muestra y hará una predicción basándose en sus clases. El valor de k puede ser elegido por el usuario y puede afectar la complejidad y precisión del modelo.
Un valor más pequeño de k puede llevar a un modelo con un menor sesgo pero una mayor varianza, mientras que un valor más grande de k puede llevar a un modelo con un mayor sesgo pero una menor varianza. En general, es una buena idea probar varios valores de k para ver cuál da el mejor rendimiento en los datos de entrenamiento y prueba. También es común usar valores impares de k para evitar empates en la predicción de las clases.
Uno de los beneficios del algoritmo K-Nearest Neighbors es que tiene un tiempo de entrenamiento bajo, ya que no requiere un modelo complejo para ajustarse a los datos de entrenamiento. En su lugar, simplemente almacena los datos de entrenamiento y realiza predicciones basándose en los K vecinos más cercanos a una muestra cuando se le pide clasificar nuevos datos. Esto significa que el tiempo de entrenamiento es esencialmente constante, independientemente del tamaño del conjunto de datos de entrenamiento.
A pesar de su simplicidad, KNN todavía puede lograr una alta precisión en muchas tareas, especialmente cuando el número de características es bajo y las clases están bien separadas. También es un algoritmo robusto que no es sensible a la escala de las características ni a la presencia de ruido en los datos. Sin embargo, puede ser sensible al valor de K y es posible que su desempeño se vea comprometido cuando el número de características es alto o cuando las clases no están bien separadas.
¿Cómo funciona el algoritmo KNN?
Para ilustrar el funcionamiento de KNN voy a presentar algunas imágenes con un caso hipotético de clasificación de datos. Supongamos que tenemos el siguiente conjunto de datos cualquiera en un plano cualquiera:

Cada «x» representa un dato en el plano espacial. Ahora supongamos que a mi, como ser humano, se me pide que clasifique los datos en grupos. Creo que todos estaremos de acuerdo en que hay dos grupos principales de datos, más o menos separados a la mitad del plano horizontal.
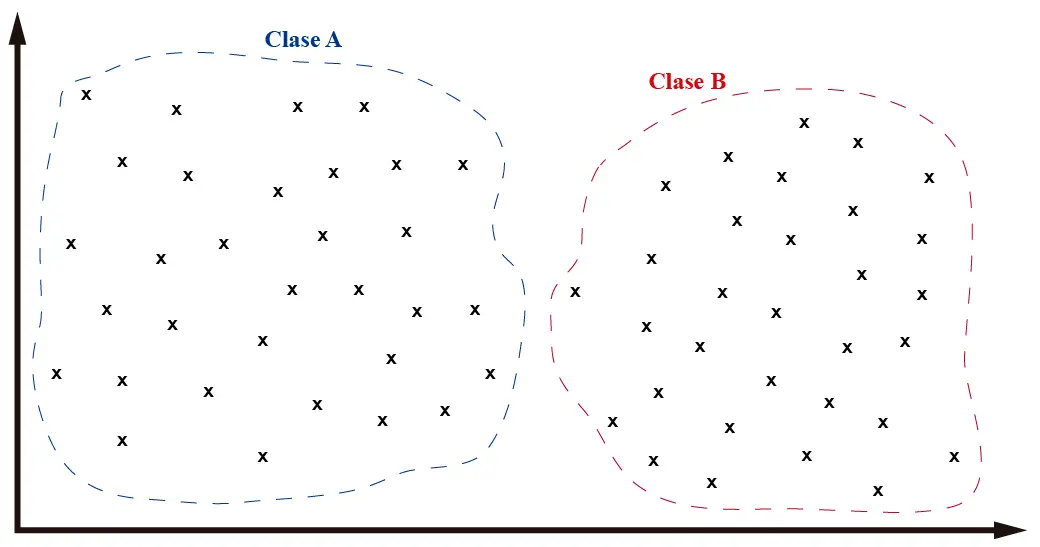
Como vemos en la imagen, hemos separado los datos en dos grupos. Cuando en Machine Learning trabajamos con conjuntos de datos no hablamos de grupos o conjuntos, sino de clases. Y cada clase puede ser representativa de cualquier objeto en el mundo real. En mi caso, voy a considerar que los objetos de la «clase A» son cuadrados y los objetos de la «clase B» son círculos.

En el momento en el que yo, un ser humano, decidí clasificar los objetos del conjunto de datos en dos clases y le asigné una clase a cada muestra, lo que hice fue construir un dataset de entrenamiento. Con este dataset podemos entrenar un clasificador de Machine Learning que nos permita clasificar nuevos datos que aún no conocemos.
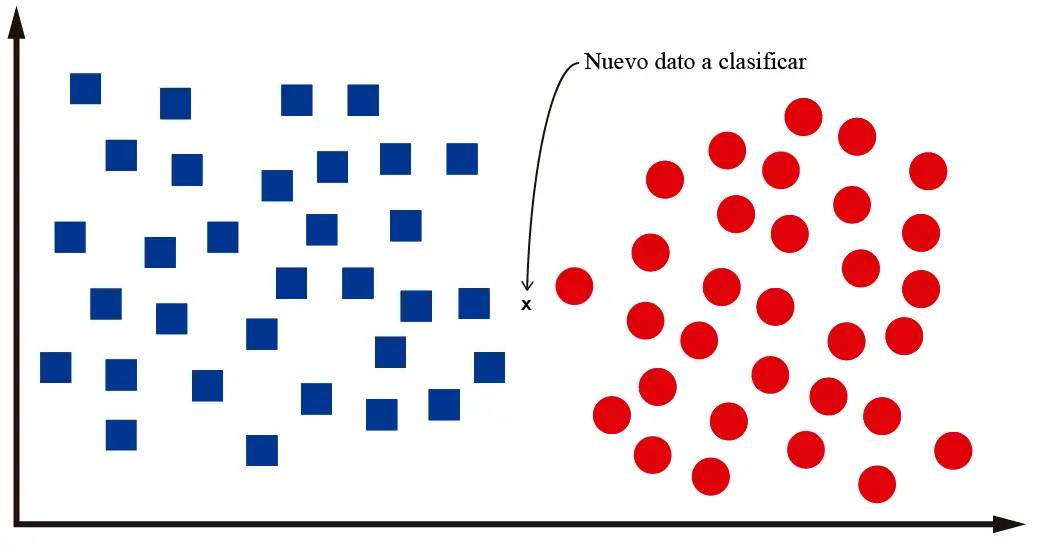
Por ejemplo, supongamos que luego de entrenar nuestro algoritmo de clasificación se nos pide que clasifiquemos un nuevo dato:
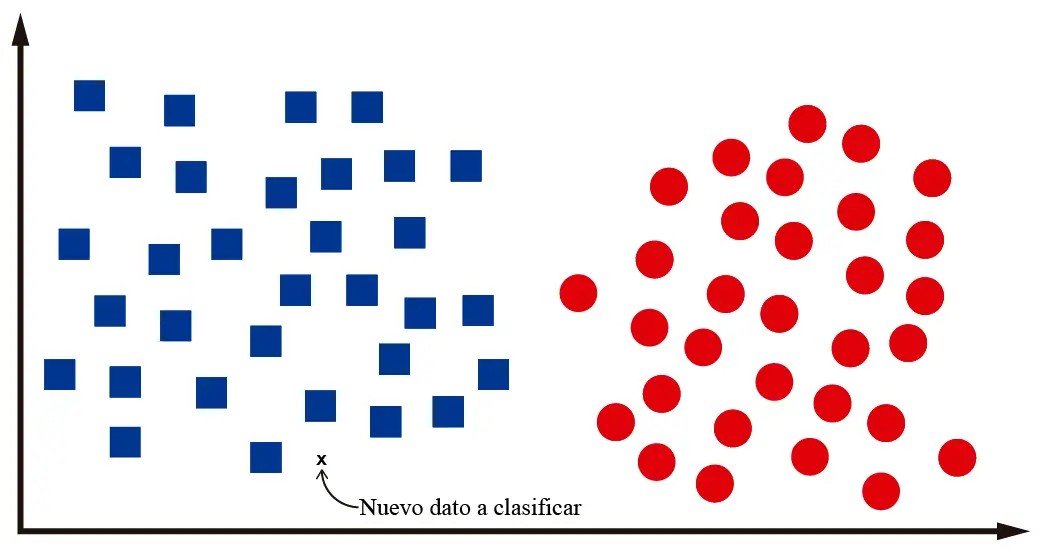
Nosotros como humanos podemos identificar que ese nuevo dato es un cuadrado. Es decir, está en medio de un montón de cuadrados. Para clasificarlo como un círculo debe estar más hacia la parte de la derecha del plano, donde están los otros círculos. ¿No es tan difícil, no?
Pero, ¿cómo hacemos para que un programa en una computadora logre clasificar este dato de manera correcta? ¿cómo hacemos que la computadora «razone» como nosotros los humanos?. Bueno, la verdad es que no lograremos que la computadora razone. Pero si le podemos enseñar a discriminar entre cuadrados y círculos a través de un algoritmo de Machine Learning.
Cada algoritmo con el que contamos hoy en día resuelve este problema de una manera distinta. En el caso del KNN, lo que haremos será identificar los «k» vecinos más cercanos al dato que queremos clasificar. De esa forma la computadora podrá determinar la proximidad del dato con respecto a las dos clases disponibles y decidir si pertenece a la una o a la otra.
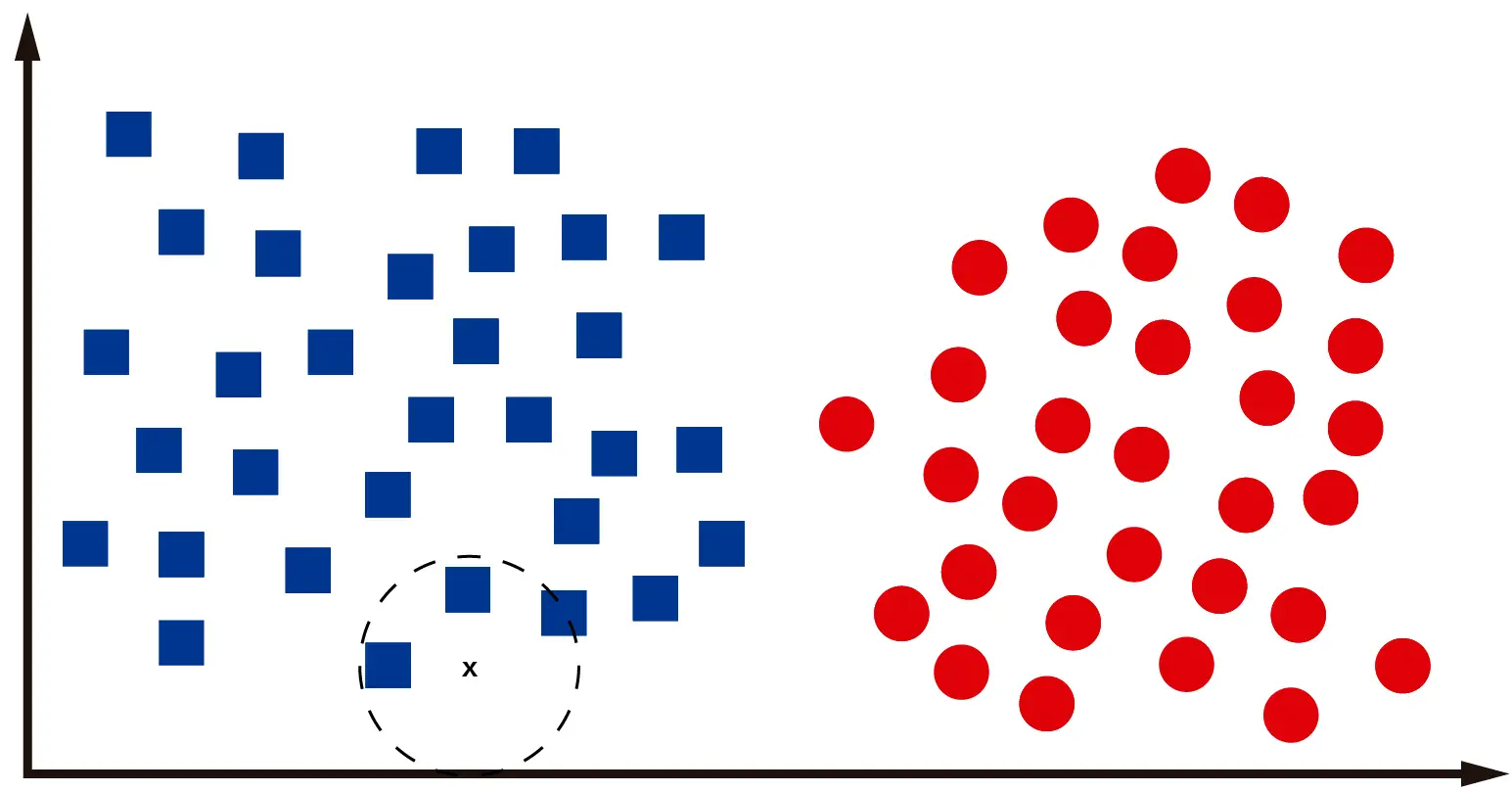
Como vemos en la imagen, los 3 «vecinos» más cercanos al dato que queremos clasificar son cuadrados. Por lo tanto, es muy probable que la «x» en la imagen represente un cuadrado. Nótese que he utilizado la palabra «probable», pues el paradigma de Machine Learning está basado en probabilidades más que en certezas.
Al estar este método basado en la verificación de los «vecinos» de un dato resulta lógico que el algoritmo KNN se llame así. K-Nearest Neighbors significa k-vecinos más cercanos. Creo que KNN es la representación computacional del «dime con quien andas y te diré quien eres».
¿Qué pasa cuando necesitamos clasificar un dato que se ubica en medio de las dos clases? Veamos la siguiente imagen:
En el caso del dato representado en la imagen no es fácil determinar si pertenece a una clase o a la otra. Incluso yo, como ser humano, no estoy seguro si se trata de un cuadrado o círculo. En el caso de la computadora, lo que hará será revisar los «k» vecinos más cercanos, calculando la distancia entre los centroides de los vecinos y el nuevo dato que se quiere clasificar. Si trabajamos con k=3, tendremos algo como esto:
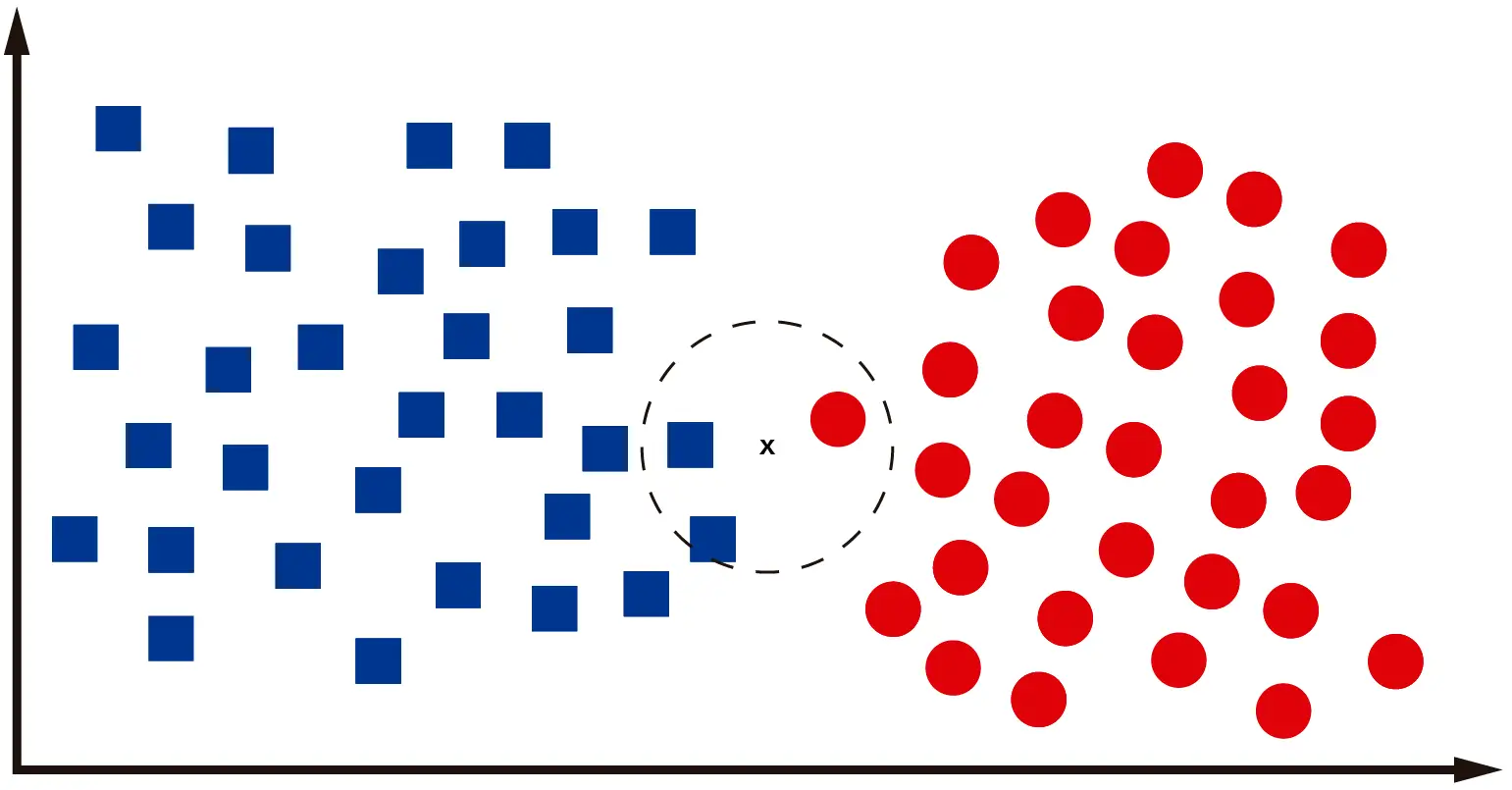
Claramente el dato es un cuadrado, pues entre sus 3 vecinos más cercanos, dos son cuadrados. Si hay un empate, donde dos o más clases tienen el mismo número de ocurrencias entre los K vecinos más cercanos, entonces se puede asignar la muestra a la clase con el valor de índice más bajo.
Este método de clasificación se conoce como votación mayoritaria, ya que la clase de la muestra se determina en base a la clase mayoritaria entre sus vecinos. Es un método simple y efectivo para la clasificación y es fácil de entender e implementar.
De manera muy general, así es como funciona el algoritmo KNN. Hay otros hiperparámetros importantes a tomar en cuenta con este algoritmo, aparte de la cantidad de vecinos que se considerará en la clasificación:
- weights: Este hiperparámetro controla cuánto peso se le da a los vecinos más cercanos en la clasificación, con las opciones siendo ‘uniform’ (todos los vecinos tienen el mismo peso) o ‘distance’ (los vecinos tienen pesos proporcionales al inverso de su distancia).
- algorithm: Este hiperparámetro controla el algoritmo utilizado para la búsqueda de vecinos más cercanos. Las opciones incluyen ‘brute’, que utiliza una búsqueda por fuerza bruta, ‘kd_tree’, que utiliza una estructura de datos KD-tree para una búsqueda más rápida, y ‘ball_tree’, que utiliza un árbol de búsqueda para una búsqueda más rápida.
- leaf_size: Este hiperparámetro controla el número de muestras en una hoja de un árbol KD o ball. Puede afectar la velocidad de la búsqueda de vecinos más cercanos.
- p: Este hiperparámetro controla la métrica de distancia utilizada para la búsqueda de vecinos más cercanos. Las opciones incluyen p=1 para la distancia de Manhattan y p=2 para la distancia Euclidiana.
Si quieren saber más sobre la matemática detrás de este modelo, los invito visitar mi post sobre modelado matemático del algoritmo KNN.
Optimización de hiperparámetros
Mi interés por el K-Nearest Neighbors nace luego mi publicación anterior en la que realizamos pruebas con distintos tipos de clasificadores sobre el dataset MNIST. KNN obtuvo una precisión relativamente alta (96.82%), aunque inferior a otros algoritmos como Support Vector Machine (97.85%) y Random Forest (96.97%). Sin embargo, hay algo en lo que KNN demostró ser uno de los mejores:
- KNeighborsClassifier | training time: 0.18 seconds, testing time: 6.30 seconds, 96.64%
- RandomForestClassifier | training time: 46.06 seconds, testing time: 0.43 seconds, 96.97%
- SVC | training time: 167.80 seconds, testing time: 85.12 seconds, 97.85%
El tiempo de entrenamiento es supremanente inferior al de los algoritmos que lograron un mejor performance en MNIST. Eso me llevó a interesarme un poco más en este algoritmo, pues es posible que con un poco de optimización de hiperparámetros se logren mejores resultados.
Así que escribí el siguiente script, basado en nuestra publicación sobre optimización de hiperparámetros:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
from sklearn.model_selection import GridSearchCV import pandas as pd import numpy as np from sklearn.neighbors import KNeighborsClassifier """ Here I set the global variables, which will be used to test the computing time for both training and testing """ def loadDataset(fileName, samples): # A function for loading the data from a dataset (MNIST) x = [] # Array for data inputs y = [] # Array for labels (expected outputs) train_data = pd.read_csv(fileName) # Data has to be stored in a CSV file, separated by commas y = np.array(train_data.iloc[0:samples, 0]) # Labels column x = np.array(train_data.iloc[0:samples, 1:]) / 255 # Division by 255 is used for data normalization return x, y # Define the grid of hyperparameter values to search over param_grid = { 'n_neighbors': [3, 5, 7, 9, 11], 'weights': ['uniform', 'distance'], 'leaf_size': [5, 10, 20, 30, 35, 40, 45, 50] } # Define the scoring metric to use for evaluation scoring = 'accuracy' # Create a GridSearchCV object clf = KNeighborsClassifier() grid_search = GridSearchCV(estimator=clf, param_grid=param_grid, scoring=scoring, cv=2, verbose=2) train_x,train_y = loadDataset("../../../../datasets/mnist/mnist_train.csv",50000) test_x,test_y = loadDataset("../../../../datasets/mnist/mnist_test.csv",10000) # Fit the grid search object to the training data grid_search.fit(train_x, train_y) # Print the best hyperparameters and the best score print("Best hyperparameters:", grid_search.best_params_) print("Best score:", grid_search.best_score_) # Re-train the model with the best hyperparameters best_clf = grid_search.best_estimator_ best_clf.fit(train_x, train_y) # Test the model with the best hyperparameters on the testing data accuracy = best_clf.score(test_x, test_y) print("Testing accuracy:", accuracy) |
Este algoritmo lo pueden descargar desde nuestro repositorio de Github. El resultado de este algoritmo debe ser algo así:
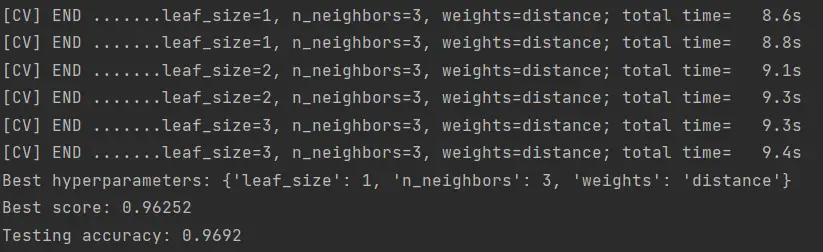
Luego de probar distintas combinaciones de parámetros se logró obtener un 96.92% de precisión en la clasificación del MNIST, utilizando los parámetros mostrados en la imagen.
El tiempo que tarda cada prueba es relativamente corto, unos 9 segundos. Llegué a probar hasta 200 combinaciones y conforme bajaba el número de vecinos, mejores resultados obtenía. It is what it is.
Conclusiones
En resumen, en este post hemos explorado el uso del algoritmo de K-Nearest Neighbors para la clasificación de imágenes en el conjunto de datos MNIST. Hemos visto que KNN es un método de clasificación no paramétrico que tiene un tiempo de entrenamiento bajo y puede lograr una alta precisión en muchas tareas. También hemos visto cómo usar la librería scikit-learn en Python para entrenar y evaluar un modelo KNN y realizar una búsqueda de hiperparámetros para encontrar la mejor combinación de parámetros.
Espero que hayas disfrutado leyendo este post y hayas aprendido algo nuevo sobre el uso del algoritmo K-Nearest Neighbors para la clasificación de imágenes. Si tienes alguna pregunta o comentario, no dudes en dejar un mensaje a continuación. ¡Gracias por leer!